Complete Solutions to MCQs of chapter INTERFERENCE AND DIFFRACTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | INTERFERENCE AND DIFFRACTION |
| MARVEL | MCQs |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The optical path difference between two identical light waves arriving at a point is 31.5 `lamda`, where `lamda` is the wavelength of light. The point is
View SolutionThe distance of a point on a screen from two coherent light sources differs by 93 wavelengths. If the path difference is 0.0465 mm, then the wavelength of light used is
View SolutionThe displacement of two interfering light waves are given by `y_(1)=3 sinomegat,y_(2)=4 sin(omegat+pi//2)`. The amplitude of the resultant wave is
View SolutionThe displacement of two coherent light waves are given by `y_(1)=a_(1)cosomegat and y_(2)=a_(2)cos(pi//2-omegat)`. The resultant intensity is given by
View SolutionTwo coherent sources of wavelength `4.8xx10^(-7)m` m produce steady interference pattern. The path difference corresponding to 10th order maximum will be
View SolutionFour independent waves are expressed as
`y_(1)=a_(1)sinomegat." "y_(2)=a_(2)sin2omegat`,
`y_(3)=a_(3)cosomegat," "y_(4)=a_(4)sin(omegat+pi//3)`.
A steady interference patternn cann be otained by using
View SolutionIf the ratio of the intensities of two waves producing interference is 9:4, then the ratio of the resultant maximum and minimum intensities will be
View SolutionTwo monochromatic sources of light A and B of wavelengths 5500 Å and 4400 Å respectively are used simultanesouly to produce interference bands on a screen. Which orders of the fringes in the two interference patterns will coincide?
View SolutionIf the ratio of the amplitudes of two interfering wave is 4:3, then the ratio of the maximumum and minimum intensities in the interference pattern is
View SolutionThe amplitude ratio of two superposing waves 3:1. what is the ratio of the maximum and minimum intensities?
View SolutionTwo waves gives by `y_(1)=10sinomegat` cm and `y_(2)=10sin(omegat+(pi)/(3))` cm are superimposed. What is the amplitude of the resultannt wave?
View SolutionThe optical path difference between two waves starting from a monochromatic source of light is `(100.5)lamda`. If the path difference between the waves is 60.3 micron, the wavelength of light used is
View SolutionIf two waves represented by `y_(1)=4sinomegat` and `y_(2)=3sin(omegat+(pi)/(3))` interfere at a point find out the amplitude of the resulting wave
View SolutionTwo coherent sources of intensities `I_1` and `I_2` produce an interference pattern. The maximum intensity in the interference pattern will be
View SolutionAn interference pattern has maximum and minimum intensities in the ratio of 36:1, what is the ratio of theire amplitudes?
View SolutionFind the wrong option from the following. Two beams of light will give rise to an interference pattern. If they are
View SolutionTwo light waves of amplitudes `A_(1)` and `A_(2)` superimpose with each other such that `A_(1) gt A_(2)`. The difference between maximum and minimum amplitudes is
View SolutionTo deminstrate the phenimenon of interference, we require two sources which emit radiation
View SolutionThe disntances of poinnt on the screen from two slits are `1.8xx10^(-5)m and 1.23xx10^(-5)m`. If the wavelength of light used is 6000 Å, then the number of bright or dark band formed at that point is
View SolutionIn Young's double slit experiment, a minimum is obtained when the phase difference of super imposing waves is
View SolutionIn Young's double slit experiment carried out with light of wavelength `lamda=`5000 Å, the distance between the slits is 0.2 mm and screen is 2.0 m away from the slits. The central maximum is at n=0. the third maximum will be formed at a distance x (from the central maxima) equal to
View SolutionTwo waves of equal amplitude and frequency interfere each other. The ratio of intensity when the two waves arrive in phase to that when they arrive `90^@` out of phase is
View SolutionThe optical path difference between two identical light waves arriving at a point (P) on the screen is `27xx10^(-7)m`. For P to be a dark point, the wavelength of light used should be
View SolutionLight from two coherent sources of the same amplitude A and wavelength `lambda` illuminates the screen. The intensity of the central maximum is `I_(0)`. If the sources were incoherent, the intensity at the same point will be
View SolutionTwo identical light waves, propagating in the same direction, have a phase difference `delta`. After they superpose, the intensity of the resulting wave will be proportional to
View SolutionThe waves of wavelength 6000 Å emitted by any atom or molecule must have some finite length whichis known as coherence length. For solution light, the length is 2.4 cm. what is the number of oscillations for this length?
View SolutionTwo beam of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is `(pi)/(2)` at point A and `pi` at point B. Then the difference between resultant intensities at A and B is : `(2001 , 2M)`
View SolutionTwo coherent monochromatic light beams of intensities 4/ and 9/ are superimosed the maxmum and minimum possible intenties in the resulting beam are
View SolutionTwo coherent sources of intensity ratio `alpha` interfere. In interference pattern `(I_(max)-I_("min"))/(I_(max)-I_("min"))`=
View SolutionIn Young's experiment d=1 m, D=1m, X=0.6mm, then wavelength of light used is
View SolutionIn Young's double slit experiment the ratio of intensities at the position of maxima and minima is 9/1. the ratio of amplitudes of light waves is
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the screen and the slit is 100 cm. if the width of the fringe is 5 mm, then the wavelength of monochromatic light used is
View SolutionThe path difference between two interfering light waves meeting at a point on the screen is `((87)/(2))lamda`. The band obtained at that point is
View SolutionIn a double slit or a biprism experiment, the fringe width for red colour as compared to that for violet colour is approximately
View SolutionIn Young's double slit experiment, the fringe width is found to be 0.6 mm. without distrubing anything, the whole arrangment is dipped in water of refractive index `4/3` the new fringe width will be
View SolutionLight of wavelength 5000 Å is incident on a double with and the interference fringes are formed on a screen plated at a distance of 1m from the slits. If the distance between the two consecutive dark bands is 1 mm, then the distance between the two slits is
View SolutionTwo parallel slits 1 mm apart are illuminated with light of wavelength 5000 Å, from a single slit. Interference pattern is obtained on a screen placed at 1 m from the slits, what is the distance between the first bright bannd and the seventh dark band?
View SolutionIf the distance between the screen and the sources is decreased by 25%, then the change in fringe width is
View SolutionIn Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
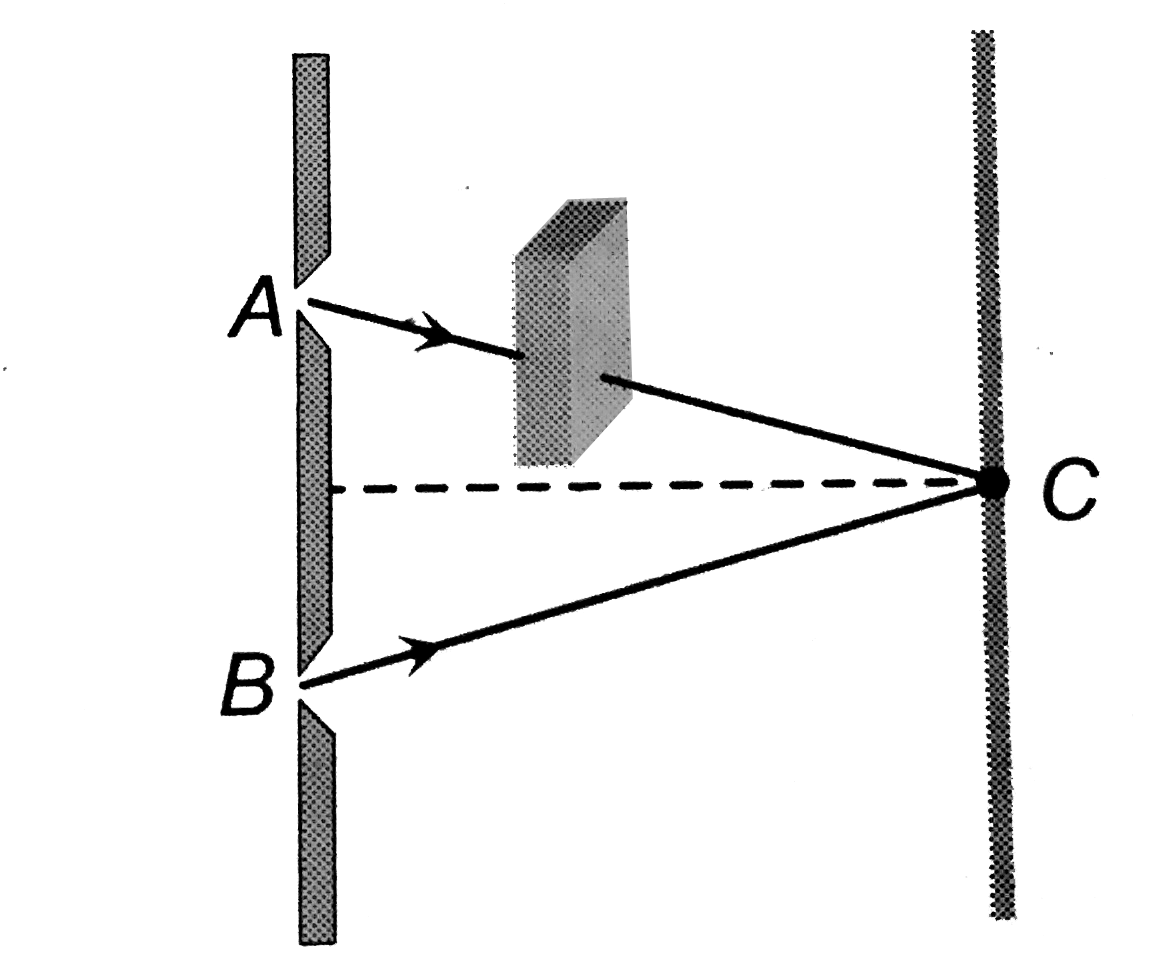
View SolutionIf white light is used in Young's double slit experiment, then a few coloured fringes can be seen
View SolutionIn a Young's double slit experiment, the separation of the two slits is doubled. To keep the samme spacing of fringes, the distance D of the screen from the slits should be made
View SolutionIn Young's double slit experiment, D=1.5m, d=4.5`xx10^(-3)m` and fringe width X=0.2 mm. what is the path difference between the interfering beams for two successive maxima
View SolutionIf the amplitude of two interfering light waves are not equal, then the intensity in the dark region formed in the interference pattern will be
View SolutionIn Young's double slit experiment, we get 15 fringes per cm on the screen, using light of wavelength 5600 Å. For the samme setting, how many fringes per cm will be obtained with light of wavelength 7000 Å?
View SolutionIn Young's double slit experiment, interference fringes eachh of width 1 mm are observed with light of wavelength 500 nm. Without distrubing the experimental arrangement, if the source is replaced by one having a wavelength 600 nm, then the fringe width will be
View SolutionIn two separate set-ups of the Young's double slit experiment, fringes of equal width are observed when lights of wavelength in the ratio of `1:2` are used. If the ratio of the slit separation in the two cases is `2:1`, the ratio of the distance between the plane of the slits and the screen in the two set-ups are
View SolutionTwo sources of light of wavelength 4500 Å annd 6000 Å are used simultaneously in Young's double slit experiment. At which order of the two wavelength pattern,s the fringes coincide?
View SolutionIn Young's double-slit experiment the angular width of a fringe formed on a distant screen is `1^(@)`. The wavelength of light used is `6000 Å`. What is the spacing between the slits?
View SolutionIn Young's double experiment, slits are kept 0.4 mm apart from each other and the screen is placed at 2 m from the slit. The fringe width for a given monochromatic source of light is 0.8 mm. if the whole set up is kept in a medium of R.I. 1.6 , the fringe width will be
View SolutionIn Young's double slit experiment using sodium light (`lamda=5898Å`) 92 fringes are seen if given colour `(lamda=5461Å)` is used how many fringes will be seen
View SolutionA thin mica sheet of thickness `2xx10^-6m` and refractive index `(mu=1.5)` is introduced in the path of the first wave. The wavelength of the wave used is `5000Å`. The central bright maximum will shift
View SolutionIn a Young's double slit esperiment, the angular width of a fringe formed on a distant screen is `1^(@)` . The slit separation is 0.01 mm. The wavelength of the light is
View SolutionThe Young's experiment is performed with the lights of blue `(lambda=4360Å)` and green colour `(lambda=5460Å)`. If the distance of the 4th fringe from the centre is x, then
View SolutionIn Young's double slit experiment, if the widths of the slits are in the ratio 4:9, the ratio of the intensity at maxima to the intensity at minima will be
View SolutionIn Young's double slit experiment, the phase difference between the light waves producing the third bright fringe from the central fringe will be (`lamda=6000` Å)
View SolutionIn Young's experiment one slit is covered with a blue filter and the other (slit) with a yellow filter then the interference pattern
View SolutionIn a Young's experiment, two coherent sources are placed `0.90mm` apart and the fringes are observed one metre away. If is produces the second dark fringe at a distance of `1mm` from the central fringe, the wavelength of monochromatic light used would be
View SolutionIn young’s double slit experiment with a source of light of wavelength `6320Å`, the first maxima will occur when
View SolutionIf the width ratio of the two slits in Young's double slit experiment is 4:1, then the ratio of intensity at the maxima and minima in the interference patternn will be
View SolutionThe path difference at a point on the screen in young's experiment is `5lamda`. The distance of that point from the central bright band is 0.5 mm. what is the bandwidth?
View SolutionTwo slits separated by a distance of 0.5 mm are illuminated by light of wavelength 5000 Å. The interference fringes are obtained on a screen at a distance of 1.2 m. what is the phase difference between two interfering waves at a point 3 mm from the central bbright fringe?
View SolutionIn a Young's double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case
View SolutionTwo slits separated by a distance of 0.5 mm are illuminated by light of wavelength 5000 Å. The interference fringes are obtained on a screen at a distance of 1.2 m. what is the phase difference between two interfering waves at a point 3 mm from the central bright fringe?
View SolutionIn a double slit experiment, the distance between the slits is increased 10 times wheares their distance from the screen is halved, then what is the new fringes width if the original fringe width is X?
View SolutionIf a torch is used in place of monochromatic light in Young's experiment what will happen?
View SolutionThe path difference produced by two waves at a point is 3.75 `mum` and the wavelength is 5000 Å. The point is
View SolutionIn young's experiment, fringes are obtained on a screen placed at a distance of 75 cm from the slits. If the separation of the narrow slits is doubled, the fringe width is decreased.
Through what distance the screen should be moved, in order to restore the spacing of the fringes?
View SolutionOn placing a thin film of mica of thickness `12xx10^(-5)cm` in the path of one of the interfering beams in young's double slit experiment using monochromatic light, the fringe pattern shifts through a distance equal to the width of a bright fringe. If `lamda=6xx10^(-5)cm`, the refractive index of mica is
View SolutionIn Young's double slit experiment, the angular width of a fringe formed on a distant screen is `0.1^(@)`. What is the spacing between the slits, if the waveelngth of light used is 6000 Å?
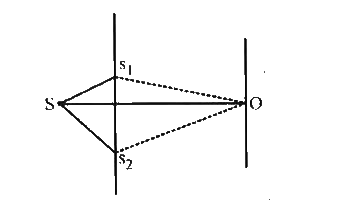
View SolutionIn an interference experiment, the two slits `S_(1) and S_(2)` are not equidistant from the source S. then the central fringe at 0 will be
View SolutionTwo coherent sources A and B of wavelenth `6xx10^(-5)cm` produce interference at ann arbitrary observation point P.
what is the path difference BP-AP if the point P is at a dark band between the third and forth order maxima?
View SolutionIn a double slit experiment, the distance between the slits is d. The screen is at a distance D from the slits. If a bright fringe is formed opposite to one of the slits, its order is
View Solutionin a two-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by `5xx10^(-2)` m towards the slits, the change in fringe width is `3xx10^(-5)`. If the distance between the slits is `10^(-3)`m, calculate the wavelength of the light used.
View SolutionIn a double slit experiment, instead of taking slits of equal widths, one slit is made twice as wide as the other then in the interference pattern.
View SolutionYong's double-slit experiment is carried out by using green, red and blue light, one color at a time. The fringe widths recorded are `beta_(G),beta_(R)` and `beta_(B)`, respectively. Then
View SolutionA beam of electron is used `YDSE` experiment . The slit width is d when the velocity of electron is increased ,then
View SolutionThe disntances of poinnt on the screen from two slits are `1.8xx10^(-5)m and 1.23xx10^(-5)m`. If the wavelength of light used is 6000 Å, then the number of bright or dark band formed at that point is
View SolutionA micture of light, consisting of wavelength 590nm and an unknown wavelength, illuminates Young's double slit and gives rise to two overlapping interference patterns on the scree. The central maximum of both lights coincide. Further, it is obseved that the third bright fringe of known light coincides with the 4th bright fringe of the unknown light. From this data, the wavelength of the unknown light is:
View SolutionYoung's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
View SolutionInterference fringes were observed in an interference chamber, where air was present.now, the chamber is evacuated and without disturbing the arrangement, intererence pattern is again obserbed. A careful observer will see
View SolutionIf the eighth bright band due to light of wavelength `lamda_(1)` and coincides with ninth bright band from light of wavelength `lamda_(2)` is young's double slit experiment, then the possible wavelength of visible light are
View SolutionThe maximum intensity of fringes in Young's experiment is I. If one of the slit is closed, then the intensity at that place becomes `I_o`. Which of the following relation is true?
View SolutionIn a Young's double slit experiment (slit distance d) monochromatic light of wavelength `lambda` is used and the figure pattern observed at a distance L from the slits. The angular position of the bright fringes are
View SolutionIn Young's double slit experiment, angular width of fringes is `0.20^(@)` for sodium light of wavelength 5890 Å. If the complete system is dipped in water, then the angular width of fringes will become
View SolutionIn Young's double slit experiment, one of the slit is wider than other, so that amplitude of the light from one slit is double of that from other slit. If `I_m` be the maximum intensity, the resultant intensity I when they interfere at phase difference `phi` is given by:
View SolutionIn Young's double slit experiment intensity at a point is `((1)/(4))` of the maximum intersity. Angular position of this point is
View SolutionIn Young's double slit experiment, the intensity on the screen at a pont where path difference `lamda` is K. what will be the intensity at the point where the path difference is `lamda/4`?
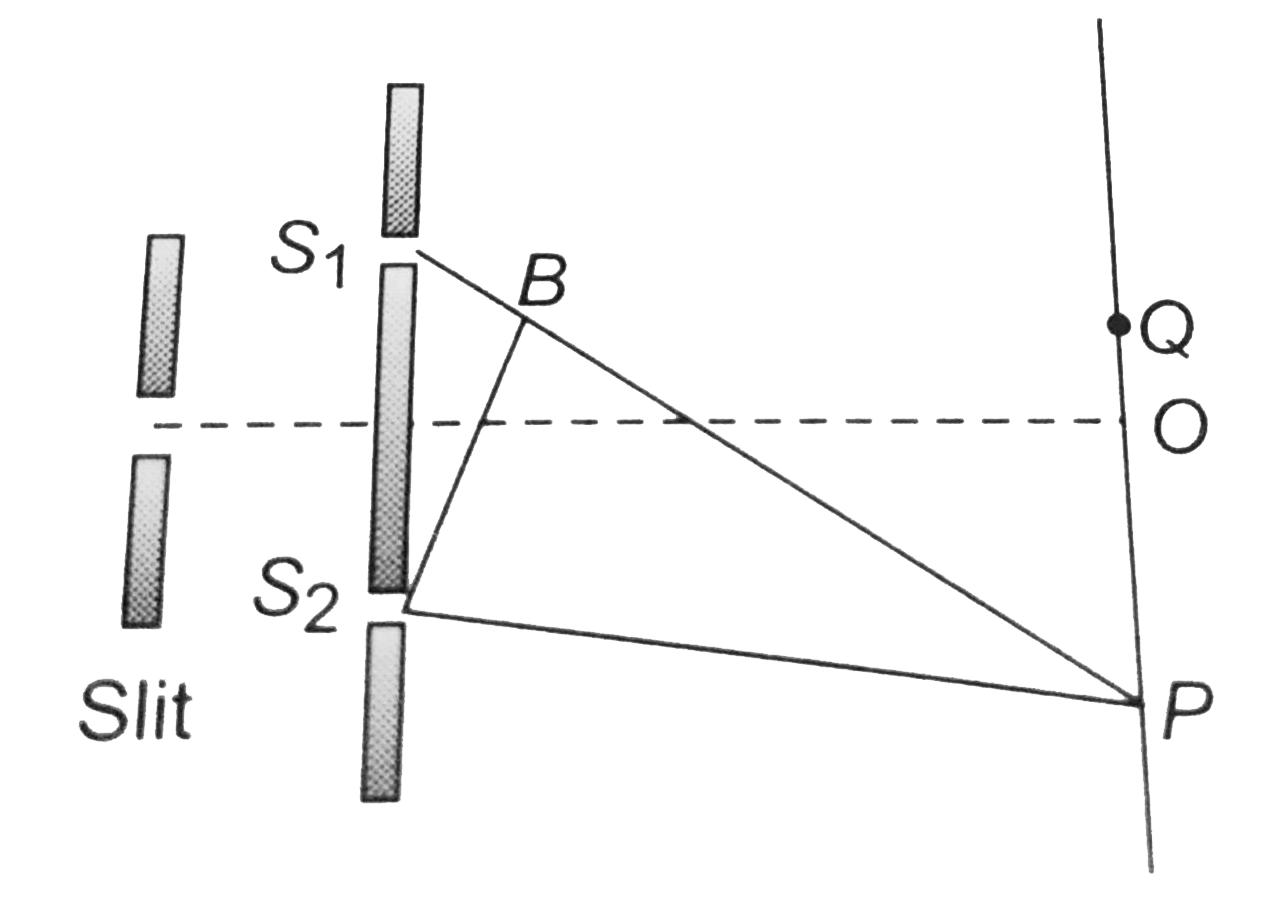
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the `11^(th)` bright fringe on the other side, as measured from Q. If the wavelength of the light used is `600 nm`. Then `S_(1)B` will be equal to
View SolutionIn Young's double-slit experiment, the two slits act as coherent sources of equal amplitude `A` and of wavelength `lamda`. In another experiment with the same set-up the two slits are sources of equal amplitude `A ` and wavelength `lamda`, but are incoherent. The ratio of the intensity of light at the midpoint of the screen in the first case to that in the second case is....
View SolutionIn double slit experiment fringes are obtained using light of wavelength `4800 Å` One slit is covered with a thin glass film of refractive index. `1.4` and another slit is covered by a film of same thickness but refractive index `1.7`. By doing so, the central fringe is shifted to fifth bright fringe in the original pattern. The thickness of glass film is
View SolutionThe maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is
View SolutionIn the Young's double slit experiment, the ratio of intensities of bright and dark fringes is 9. this means that
View SolutionA Young's double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is
View SolutionIn Young's double slit experiment, the intensity at a point where the path difference is `lamda/6` (`lamda` is the wavelength of light) is I. if `I_(0)` denotes the maximum intensities, then `I//I_(0)` is equal to
View SolutionWhen a transparent film of refractive index 1.5 is kept over one of the openings of a double slit experiment apparatus, the interference pattern is shifted through six successive maxima, towards the side, where the film was placed. What is the thickness of the film if the wavelength of light used in 6000 Å?
View SolutionIn a Young's double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600nm is used. If the wavelength of light is changed to 400nm, number of fringes observed in the same segment of the screen is given by
View SolutionIn the ideal double-slit experiment, when a glass-plate(refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wave-length `lamda`), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and theh screen is at a distance `d (gt gtb)` from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View SolutionIn Young's double slit experiment, using monochromatic light, the fringe patternn shifts by a certain distance on the screen, when a transparent sheet of thickness 't' and refractive index `mu` is introduced in the path of one of the interfering waves. the sheet is then removed and the distance between the screen and the slits is doubled. it is found that the distance between the successive maxima (or minima) now is the samme as the observed fringe shift when the sheet was introduced. what is the wavelength of light used?
View SolutionA beam of light consisting of two wavelength `6500Å&5200Å`is used to obtain interferance fringes in a young's double slit experiment .The distance between the slits is `2.0mm` and the distance between the plane of the slits and thescreen is `120cm`,.what is the least distance from the central maximum where the bright fringes due to both the wave length coincides?
View Solution
MCQs questions and complete solutions for chapter INTERFERENCE AND DIFFRACTION of MARVEL PHYSICS (HINGLISH) of Class 12