In an interference experiment, the two slits are not equidistant from the source S. then the central fringe at 0 will be
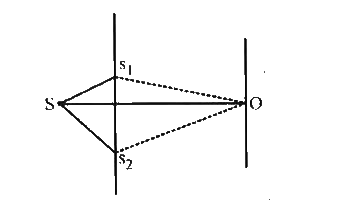
always dark
always bright
either bright or dark depending upon the position of S
neither dark nor bright
The correct Answer is:C
It depends upon the path diff. .
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP20videos
INTERFERENCE AND DIFFRACTION
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
- BOOK - MARVEL PUBLICATIONCHAPTER - KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONEXERCISE - TEST YOUR GRASP - 930videos
KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATION
Similar Questions
In a young’s double slit experiment the distance between slits S1 and S2 is d and distance of slit plane from the screen is D(>>d). The point source of light (S) is placed a distance d2 below the principal axis in the focal plane of the convex lens (L). The slits S1 and S2 are located symmetrically with respect to the principal axis of the lens. Focal length of the lens is f(>>d).
Find the distance of the central maxima of the fringe pattern from the centre (O) of the screen.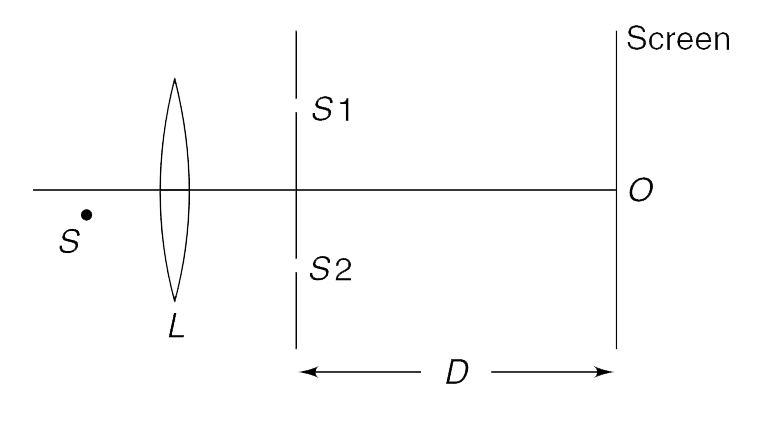
View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d
View Solution
Knowledge Check
- Question 1 - Select One
In the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
A(a) Always brightB(b) Always darkC(c) Either dark or bright depending on the position of SD(d) Neither dark nor bright - Question 2 - Select One
In an interference experiment , two parallel verticals slits S1 and S2 are used. A thin glass plate is introduced in the path of light from S1. Then
Afringe pattern remains unalteredBfringe pattern as a whole is laterally shifted towards S1Cfringe pattern as a whole is laterally shifted towards S2Dfringe width decrease. - Question 3 - Select One
_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-A3IB5IC8IDzero
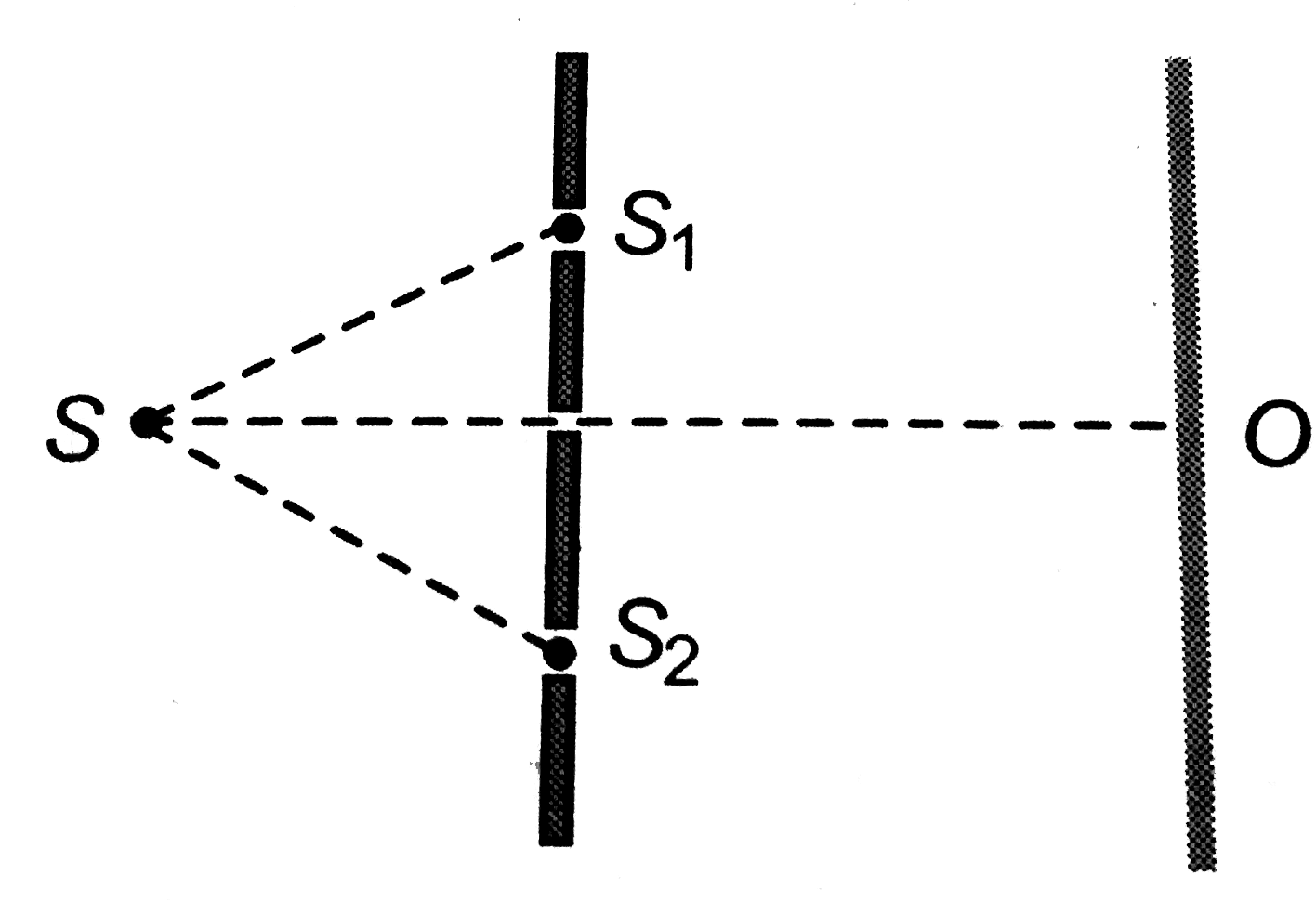
In a modified set up of Young's double slit experiment, it is given that SS2−SS1=λ4 i.e., the source S is not equidistant from the slits S1andS2.
(a) Obtain the condition for constructive and destructive interference at any point P on the screen in terms of the path difference Δ=S2P−S1P.
(b) Does the observed central bright fringe lie above or below O ? Give reason in support of your answer.View SolutionWhen light from two sources (say slits S1 and S2) interfere, they form alternate dark and bright fringes. Bright fringe is formed at all point where the path difference is an odd multiple of half wavelength. At the condition of equal amplitudes, A1=A2=a, the maximum intensity will be 4a2 and the visibility improves, The resultant intensity can also be indicated with phase factor as I=2a2cos2(ϕ/2).Using this passage, answer the following questions.
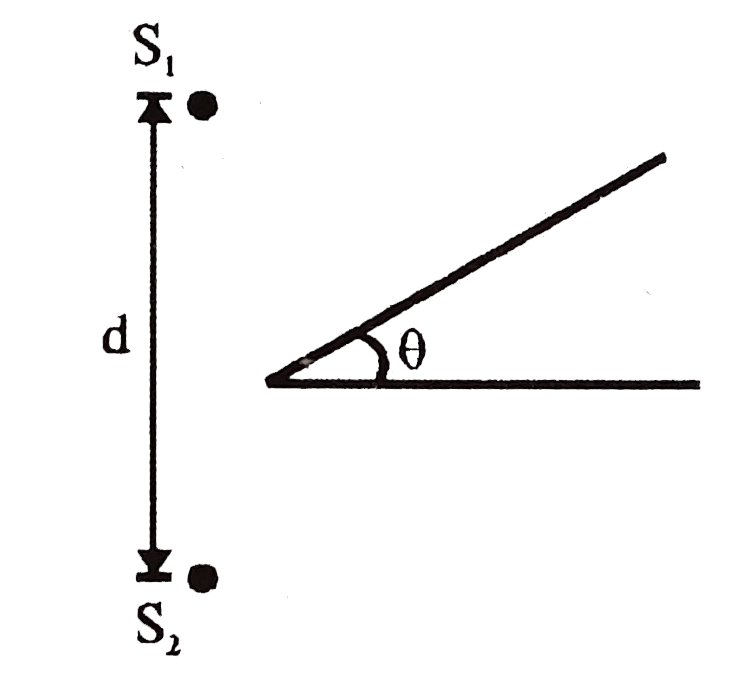
If the path difference between the slits S1 and S2 is λ2 the central fringe will have an intensity ofView SolutionIn a interference arrangement similar to Young's double-slit experiment ,the slits S1 and S2 are illuminated with coheremt microwave source ,each of frequencies 106 Hz.The source are syhronized to have zero phase difference.The slits are separated by a distance from S1 and S2 where theta is defined as shown if I0 is the maximum intensity then
View SolutionIn Young’s experiment small gap between the two slits is d, and distance of screen from the slits is D. Then the number of fringes per metre that will appear on screen by mono-chromatic source of wavelength of λ, will be :
View SolutionFringe width equal to 1 mm is observed in the interference pattern of biprism experiment. Then the distance of nearest bright fringe from the central bright fringe will be :
View Solution