Complete Solutions to PAPER II OBJECTIVE TYPE of chapter PRACTICE SET 13 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PRACTICE SET 13 |
| MHTCET PRACTICE PAPER | PAPER II OBJECTIVE TYPE |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
The shortest distance between the lines `(x-3)/3=(y-8)/(-1)=(z-3)/1a n d(x+3)/(-3)=(y+7)/2=(z-6)/4` is a. `sqrt(30)` b. `2sqrt(30)` c. `5sqrt(30)` d. `3sqrt(30)`
View SolutionThe switching function of network is
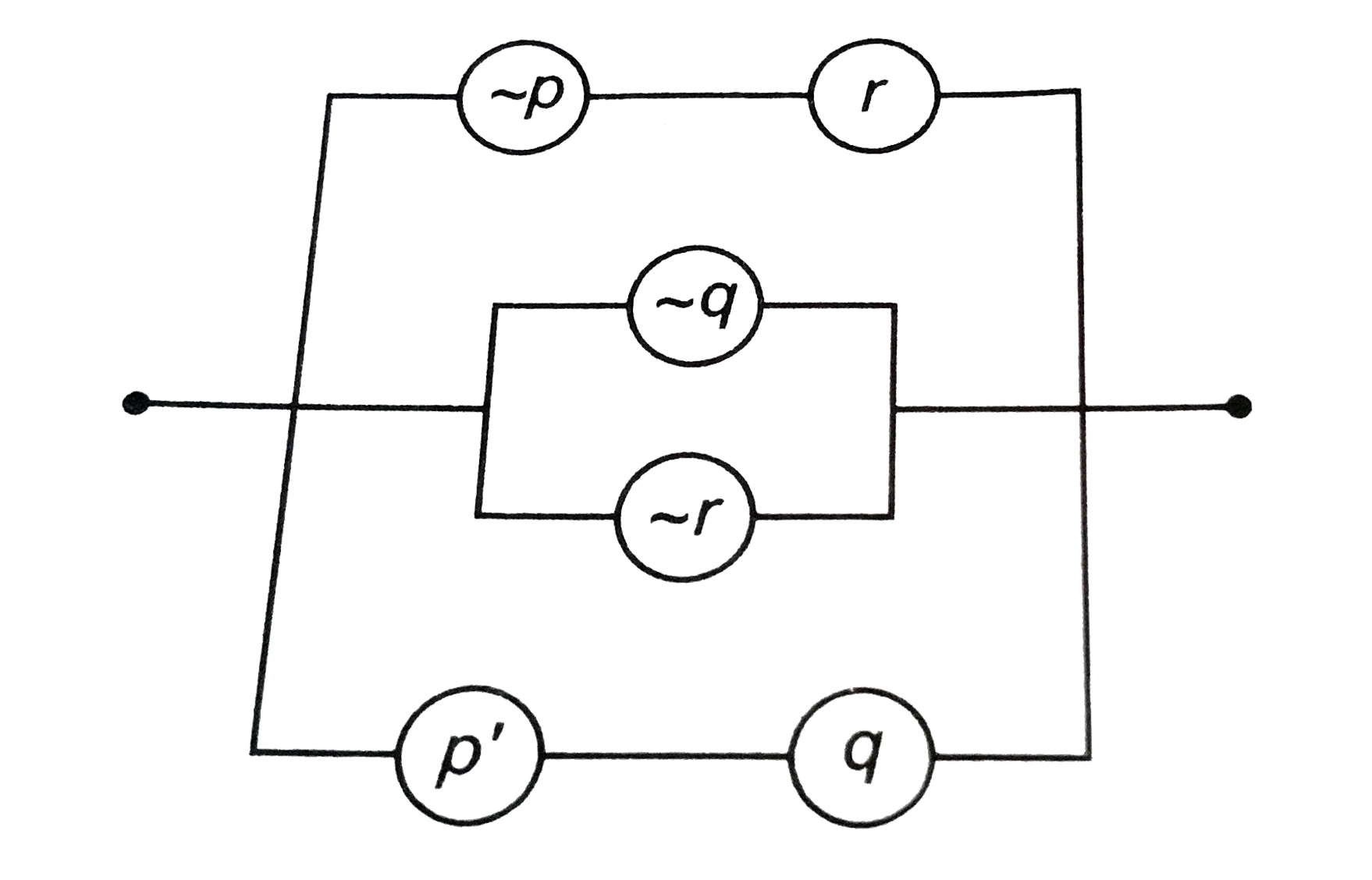
View SolutionA five digit number is formed but the digits 1,2,3,4,5 without repetition. Find the probability that the number is divisible by 4.
View SolutionIf `f(x)={sinx ,x!=npi,n in I2,ot h e r w i s e` `g(x)={x^2+1,x!=0,4,x=0 5,x=2` then `("lim")_(xvec0)g{f(x)}i s=`
View SolutionIf `f(x)=log_(x)(log_(e)x)`, then `f'(x)`at `x=e` is equal to
View SolutionThe value of `lim_(x->a)log(x-a)/(log(e^x-e^a)` is
View Solutionif `2^x+2^y=2^(x+y)` then the value of `(dy)/(dx)` at `x=y=1`
View Solution`intx^(3)log x dx `is equal to
View SolutionThe value of `int_(2)^(3)(x+1)/(x^(2)(x-1))dx` is
View Solutionif` |veca|=4, |vecb|=2` and the angle between `veca and vecb` is ` pi/6` then `(vecaxxvecb)^2` is equal to
View SolutionThe differential equation of the rectangular hyperbola whose axes are the asymptotes of the hyperbola, is
View SolutionThe statement `pvv~p` is
View SolutionIf birth to amale child and birth to a femal child are equal probable, then what is the probability that at least one of the three children born to a couple is male?
View SolutionIf `y=tan^(-1)[(sinx+cosx)/(cosx-sinx)]` then `(dy)/(dx)` is
View SolutionThe equation `12x^(2)+7xy-12y^(2)-18x+y+6=0` represents
View SolutionA focus of an ellipse is at the origin. The directrix is the line `x=4` and the eccenricityh is `1/2`, then length of semi-major axis is
View SolutionA parabola is drawn with focus at (3,4) and vertex at the focus of the parabola `y^2-12y-4y+4=0`. The equation of the parabola is
View SolutionIf a circle passes through (0,0) and (`a,0)` and `(0,b)`, then the coordinates of its centre are
View SolutionA line is drawn through the point `P(3,11)` to cut the circle `x^(2)+y^(2)=9` at A and B. Then `PA.PB` is equal to
View SolutionIf the first, second and last terms of an arithmetic series are a,b, and c respectively, then the number of terms is
View SolutionThe denominator of a fraction is greater than 16 of the square of numerator, then least value of fraction is
View SolutionThe equation of tangent to the curve `y=be^(-x//a)` at the point where it crosses Y-axis is
View SolutionThe function `f(x)=x^(-x),(x epsilonR)` attains a maximum value at `x` is
View SolutionThe mean and varaince of binomial distribution are 4 and 3, respectively. Then, the probability of getting exactly six success in this distribution is
View SolutionThe value of
`lim_(ntooo)[n/(n^(2)+1^(2))+n/(n^(2)+2^(2))+………….+n/(n^(2)+n^(2))]`, is
View SolutionThe value of `int_(-2)^(4)|x+1|dx` is equal to
View SolutionThe function `f:""R""~""{0}vecR` given by `f(x)=1/x-2/(e^(2x)-1)` can be made continuous at x = 0 by defining f(0) as (1) 2 (2) `-1` (3) 0 (4) 1
View SolutionDefine `f` on `R` into itself by `f(x)={(x"sin"1/x, "when"x!=0),(0,"when"x=0):}` then
View SolutionIf `y=x-x^2`, then the derivative of `y^2` w.r.t `x^2` is
View SolutionIf `f'(x)=g(x)` and `g'(x)=-f(x)` for all `x` and `f(2)=4=f'(2)` then `f^(2)(4)+g^(2)(4)` is
View SolutionThe point on the curve `y^(2)=x` the tangent at which makes an angle `45^(@)` with X-axis is
View SolutionThe smallest circle with centre on Y-axis and passing through the point `(7,3)` has radius
View SolutionThe function `f(x)=x(x+3)e^(-(1/2)x)` satisfies the conditions of Rolle's theorem in (-3,0). The value of c, is
View SolutionFor what values of `x` the function `f(x)=x^(4)-4x^(3)+40` si monotonic decreassing?
View SolutionIf `a` is a positive number such that the arithmatic mean of a and 2 exceeds their geometric mean by 1. Then, the value of a is
View SolutionA line passing through origin and is perpendicular to two given lines `2x+y+6=0` and `4x+2y-9=0`. The ratio in which the origin divides this line is
View SolutionIf A and B are two sets, then `(AuuB)'uu(A'nnB)` is equal to
View SolutionIf a relation `R` on the set `N` of natural numbers is defined as `(x,y)hArrx^(2)-4xy+3y^(2)=0,Aax,yepsilonN`. Then the relation `R` is
View SolutionIf `5cos2 theta+2 "cos"^(2) (theta)/2+1=0`, when `(0 lt thetaltpi)` the the value of `theta` are
View SolutionIf in `DeltaABC,a=12cm, b=12cm` and `c=5cm` then distance from a to side BC is
View SolutionThe value of `cos[2 tan^(-1)(-7)]` is
View SolutionSolution of the differential equation `x(dy)/(dx)=y+sqrt(x^(2)+y^(2))`, is
View SolutionThe differential equation satistied by the family of curves `y=axcos(1/x+b)`, where a,b are parameters, is
View SolutionThe value of `sqrt(2)int(sinx)/(sin(x-(pi)/(4)))dx` , is
View SolutionThe slope of the tangent to a curve `y=f(x)` at `(x,f(x))` is `2x+1.` If the curve passes through the point `(1,2)` then the area of the region bounded by the curve, the x-axis and the line `x=1` is (A) `5/6` (B) `6/5` (C) `1/6` (D) `1`
View SolutionThe area of the region bounded by the parabola `(y-2)^(2) = x- 1`, the tangent to the parabola at the point `(2,3)` and the x-axis is
View SolutionIf a line makes an angle of `pi/4` with the positive directions of each of x-axis and y-axis, then the angle that the line makes with the positive direction of the z-axis is (1) `pi/6` (2) `pi/3` (3) `pi/4` (4) `pi/2`
View SolutionFind the ratio in which the line joining (2,4,5) and (3,5,4) is divided by the yz-plane.
View SolutionIf a and b are the two vectors such that `|a|-3sqrt(3),|b|=4` and `|a+b|=sqrt(7)`, then the angle between a and b is
View SolutionIf `f` be a function such that `f(9)=9` and `f'(9)=3`, then `lim_(xto9)(sqrt(f(x))-3)/(sqrt(x)-3)` is equal to
View Solution
PAPER II OBJECTIVE TYPE questions and complete solutions for chapter PRACTICE SET 13 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12