Complete Solutions to Paper 2 (Mathematics) of chapter PRACTICE SET 19 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PRACTICE SET 19 |
| MHTCET PRACTICE PAPER | Paper 2 (Mathematics) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
If in a triangle `ABC,4sin A = 4 sin B=3 sin C`, then `cos C=`
View Solution`{x inR:cos2x+2cos^(2)x=2}` is equal to
View SolutionIf `theta` and `phi` are acute angles satisfying `sin theta=1/2, cos phi=1/3` then `theta+phi=`
View Solution`cot^(-1)9+cosec^(-1)(sqrt(41))/(4)=(pi)/(4)`
View SolutionThe equation of one of the curves whose slope of tangent at any point is equal to `y+2x` is `y=2(e^x+x-1)` `y=2(e^x-x-1)` `y=2(e^x-x+1)` `y=2(e^x+x+1)` (5) `y=e^x-x-1`
View Solution`(dy)/(dx) = (xy+y)/(xy+x)`, then the solution of differential equation is
View SolutionThe differential equation representing the family of curves `y^(2)=2c(x+c^(2//3))`, where c is a positive parameter, is of
View SolutionProve that the product of the matrices `[[cos^2alpha, cosalphasinalpha],[cosalphasinalpha,sin^2alpha]]` and `[[cos^2beta,cosbetasinbeta],[cosbetasinbeta,sin^beta]]` is the null matrix when `alpha and beta` differ by an odd multiple of `pi/ 2`.
View Solution`int sqrt(1+sin((x)/(4)))` dx is equal to
View SolutionArea bounded by the curves `4y = |x^2-4| and y + | x | = 7`, is equal to :
View SolutionIf `f(t)` is an odd function, then `varphi(x)=int_a^xf(t)dx` is an even function.
View SolutionIf `f(x)` is a function satisfying `f(1/x)+x^2f(x)=0` for all nonzero `x` , then evaluate `int_(sintheta)^(cos e ctheta)f(x)dx`
View SolutionThe value of `int_(3)^(5)(x^(2))/(x^(2)-4)` dx is
View SolutionThe plane `2x+3y+4z=1` meets the coordinate axis in A, B, C. The centroid of the `DeltaABC` is
View SolutionThe equation of straight line equally inclined to the axes and equidistant from the point `(1, -2)` and `(3,4)` is:
View SolutionLet `P(-1,0), Q(0,0),R(3,3sqrt(3))` be three points then the equation of the bisector of the angle `anglePQR` is :
View SolutionLet A and B be sets. If `AnnX=BnnX=phi` and `AuuX=BuuX` for some set X then how that A=B
View SolutionLet `R={(3,3),(6,6),(9,9),(12,12),(6,12),(3,9(,(3,12),(3,6)}` be relation on the set `A={3,6,9,12}`. The relation is-
View SolutionThe first four terms of an AP are a, 9, `3a- b, 3a+b`.
The 2011 th term of an AP is
View SolutionThe shortest distance between the straight lines
`(x-6)/(1)=(2-y)/(2)=(z-2)/(2)" and "(x+4)/(3)=(y)/(-2)=(1-z)/(2)` is
View SolutionAn urn contains 4 white and 3 red balls. Three balls are drawn with replacement from this urn. Then, the standard deviation of the number of red balls/drawn is
View SolutionTwo aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is (1) 0.06 (2) 0.14 (3) 0.2 (3) 0.7
View SolutionIf `y="log"_(2)"log"_(2)(x)`, then `(dy)/(dx)` is equal to
View SolutionIf `A=[(1,2,-1),(-1,1,2),(2,-1,1)]`, then det (adj(adj A) is
View SolutionDual of `x ^^(y vv x)=x` is
View SolutionIf given constraints are `5x+4y ge2, x le6, y le 7`, then the maximum value of the function `z=x+2y` is
View SolutionThe angle between the pair of straight lines `y^(2)sin^(2)theta-xy sin^(2)theta+x^(2)(cos^(2)theta-1)=0` is
View SolutionThe normal to the curve `x=a(cos theta + theta sin theta), y=a(sin theta - theta cos theta)` at any `theta` is such that
View SolutionIf `f(x)={(x^(alpha)logx , x > 0),(0, x=0):}` and Rolle's theorem is applicable to `f(x)` for `x in [0, 1]` then `alpha` may equal to (A) -2 (B) -1 (C) 0 (D) `1/2`
View Solutionif the line `xcosalpha+ysinalpha=p` is normal to the ellipse `x^2/a^2+y^2/b^2=1` then
View Solution`int sec^(8//9)x cosec^(10//9)x ` dx is equal to
View SolutionSwitching function of the network is
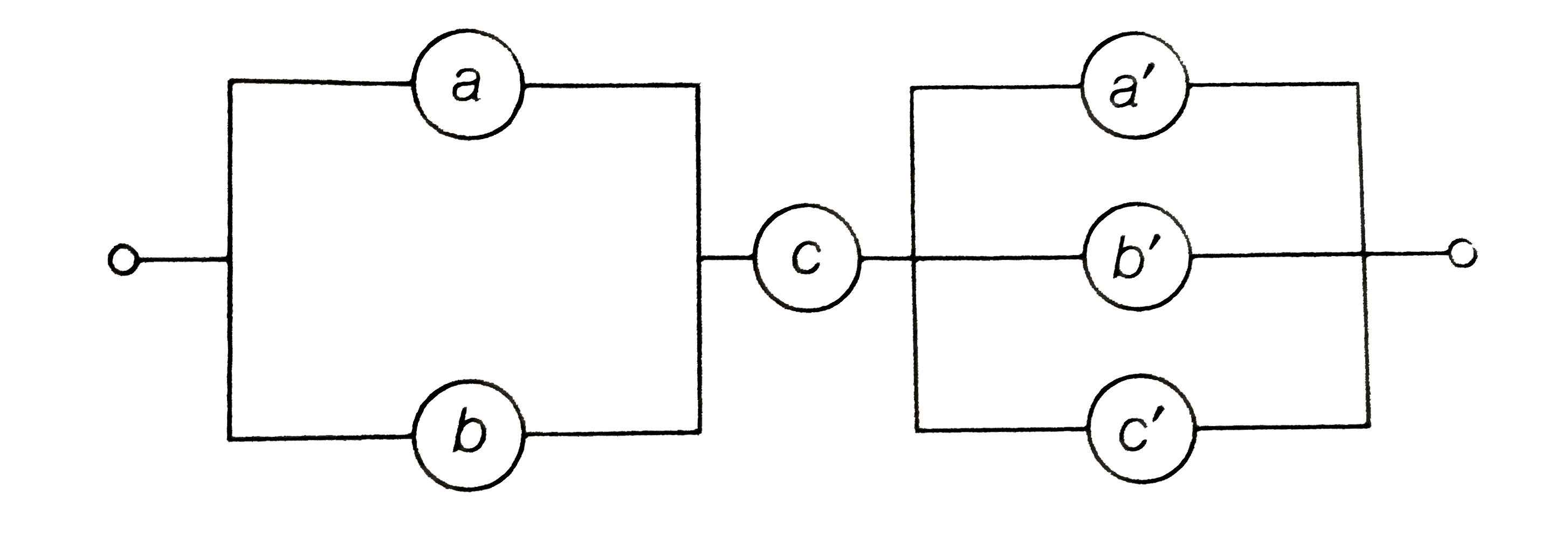
View SolutionFind the equation of the plane containing the lines `(x-5)/4=(y-7)/4=(z+3)/(-5)a n d(x-8)/7=(y-4)/1=(z-5)/3dot`
View SolutionIf `bar a,bar b,bar c` are non coplanar vectors and `lambda` is a real number then `[lambda(bar a+bar b)lambda^2 bar b lambda bar c]=[bar a bar b+bar c bar b]` for
View SolutionIf the vectors `vec(AB)=3hati+4hatk and vec(AC)=5hati-2hatj+4hatk` are the sides of a triangle ABC, then the length of the median through A is (A) `sqrt(33)` (B) `sqrt(45)` (C) `sqrt(18)` (D) `sqrt(720`
View Solution`"I f"int(dx)/(cos^3xsqrt(sin2x))=a(tan^2x+b)sqrt(tanx)+c`
View SolutionArea bounded by the curve `y=sin^(2)x` and lines `x=(pi)/(2),x=pi` and X-axis is
View SolutionIf p and q are two statements, then `(p rArr q) iff (~q rArr ~ p)` is
View SolutionInequation `y-x le 0` represents
View SolutionThe 5th term of the series `(10)/(9),(1)/(3)sqrt((20)/(3)),(2)/(3),…` is
View SolutionLet (x,y) be any point on the parabola `y^2 = 4x`. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionEquation of the ellipse whose foci are `(2, 2) and (4, 2)` and the major axis is of length `10` is
View Solution`(sin5theta+sin3theta)/(cos5theta+cos3theta)` is equal to
View SolutionFor the two circles `x^2+y^2=16 and x^2+y^2-2y=0`, there is/are
View SolutionConsider the inequalities `x_(1)+x_(2)le3,2x_(1)+5x_(2)ge10x_(1),x_(2)ge0` which of the following point does not lie in the feasible region ?
View SolutionSuppose the cubic `x^(3)-px+q` has three distinct real roots, where `pgt0` and `qgt0`. Then which one of the following holds?
View SolutionIf `f(x+y)=f(x)f(y)` for all real x and y, `f(6)=3` and `f'(0)=10`, then f'(6) is
View SolutionA ladder 10 m long rests against a vertical wall with the lower end on the horizontal ground. The lower end of the ladder is pulled along the ground away from the wall at the rate of 3 m/s. The height of the upper end while it is descending at the rate of 4 m/s, is
View SolutionIf `ax^(2)+bx+4` attains its minimum value -1 at x = 1, then the values of a and b are respectively
View SolutionThe equation of the tangent to the curve ` y=(2x-1)e^(2(1-x))` at the point of its maximum, is
View Solution
Paper 2 (Mathematics) questions and complete solutions for chapter PRACTICE SET 19 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12