Complete Solutions to Exercise 2 (MISCELLANEOUS PROBLEMS) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| MHTCET PREP GUIDE | Exercise 2 (MISCELLANEOUS PROBLEMS) |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
If a random variable X has the following probability distribution values of X
Then `P(Xge6)` is equal to

View SolutionLet X is a continuous random variable with probability density function
`f(x)={{:(x/6+k,0lexle3),(0," otherwise"):}`
The value of k is equal to
View SolutionA random variable X has the probability distribution given below
Its variance is

View SolutionIf the pdf of a curve X is `f(x)={{:(k.e^(-thetax)","thetagt0","0lexltoo),(0","-ooltxlt0" then k is equal to"):}`
View SolutionA random variable X takes values 1,2,3 and 4 with probabilities `(1)/(6),(1)/(3),(1)/(3),(1)/(6)` respectively, then its mean and variance is equal to
View SolutionA function is defined as `f(x)={{:(0","" for "xgt2),((2x+3)/(18)" for "2lexle4),(0" for "xgt4):}`
Then `P(2ltXlt3)` is
View SolutionA random variable has the following probability distribution
The value of p is

View SolutionA random variable X has the following probability distribution
The mean and standard deviation if X are rspectively
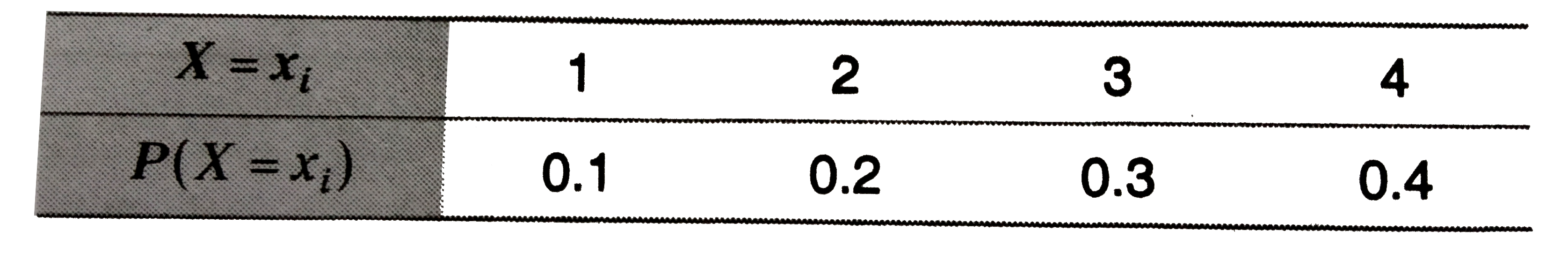
View SolutionIf X is a random variable with distribution given below
The value of k and its variance are

View SolutionIf a curve X has probability density function (pdf)
`f(x)={{:(ax","0lexle1),(a","1lexle2),(3a-ax","2lexle3),(0",""otherewise"):}`
Then, a is equal to
View SolutionFor a random variable X, if E(X) = 5 and V(X) = 6, then `E(X^2)` is equal to
View Solutionprobability distribution of a random variable X is
If `a=P(Xge2) and b=P(Xlt3)` then

View SolutionThe pdf of a curve X is
`f(x)={{:(k/sqrtx","0ltxlt4),(0","xle0" or "xge4):}`
Then , `P(Xge1)` is equal to
View SolutionThe random variable X has the following probability distribution
Then, F(0) is equal to

View SolutionThe probability distribution of the random variable X is given by
Then, the value of V(X) is equal to

View SolutionIf the pdf of a curve X is
`f(x)={{:(3(1-2x^2)","0ltxlt1),(0","xle0" or "xge1):}`
Then, the cdf of X is equal to
View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are

View SolutionIf random variable X has the following probability distribution. Then the value of a is

View SolutionA random variable X is defined by
`X={{:("3 with probability"=1/3),("4 with probability"=1/4),("12 with probability"=5/(12)"):}`
Then, E(X) is
View SolutionThe life in hours of a ratio tube is continuous random variable with pdf `f(x)={{:((100)/x^2","xge100),(0",""else where"):}` Then, the probability that the life of tube will be less than 200 h if it is known that the tube is still functioning after 150 h of services is
View SolutionIf a random variable X has the following probability distribution values of X
Then `P(Xge6)` is equal to

View SolutionLet X is a continuous random variable with probability density function
`f(x)={{:(x/6+k,0lexle3),(0," otherwise"):}`
The value of k is equal to
View SolutionA random variable X has the probability distribution given below
Its variance is

View SolutionIf the pdf of a curve X is
`f(x)={{:(k.e^(-thetax)","thetagt0","0lexltoo),(0","ooltxlt0" then k is equal to"):}`
View SolutionA random variable X takes values 1,2,3 and 4 with probabilities `(1)/(6),(1)/(3),(1)/(3),(1)/(6)` respectively, then its mean and variance is equal to
View SolutionA function is defined as `f(x)={{:(0","" for "xgt2),((2x+3)/(18)" for "2lexle4),(0" for "xgt4):}`
Then `P(2ltXlt3)` is
View SolutionA random variable has the following probability distribution
The value of p is

View SolutionA random variable X has the following probability distribution
The mean and standard deviation if X are rspectively
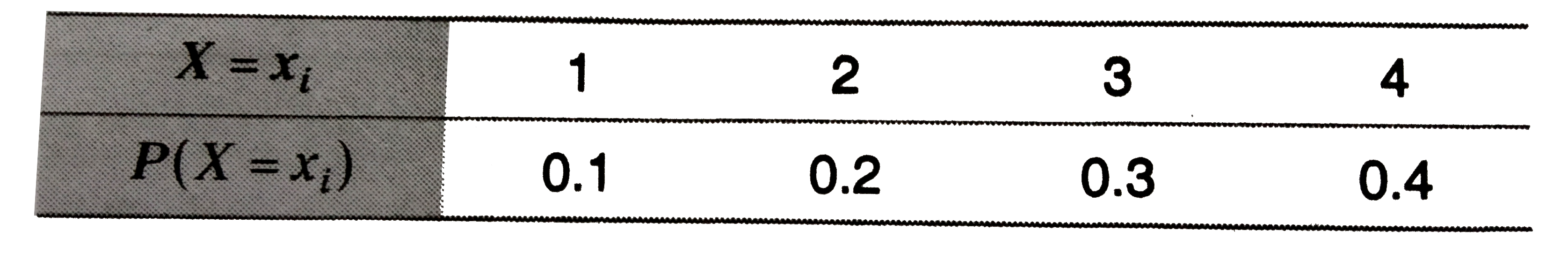
View SolutionIf X is a random variable with distribution given below
The value of k and its variance are

View SolutionIf a curve X has probability density function (pdf)
`f(x)={{:(ax","0lexle1),(a","1lexle2),(3a-ax","2lexle3),(0",""otherewise"):}`
Then, a is equal to
View SolutionFor a random variable X, if E(X) = 5 and V(X) = 6, then `E(X^2)` is equal to
View Solutionprobability distribution of a random variable X is
If `a=P(Xge2) and b=P(Xlt3)` then

View SolutionThe pdf of a curve X is
`f(x)={{:(k/sqrtx","0ltxlt4),(0","xle0" or "xge4):}`
Then , `P(Xge1)` is equal to
View SolutionThe random variable X has the following probability distribution
Then, F(0) is equal to

View SolutionThe probability distribution of the random variable X is given by
Then, the value of V(X) is equal to

View SolutionIf the pdf of a curve X is
`f(x)={{:(3(1-2x^2)","0ltxlt1),(0","xle0" or "xge1):}`
Then, the cdf of X is equal to
View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are

View SolutionIf random variable X has the following probability distribution. Then the value of a is

View SolutionA random variable X is defined by
`X={{:("3 with probability"=1/3),("4 with probability"=1/4),("12 with probability"=5/(12)"):}`
Then, E(X) is
View SolutionThe life in hours of a ratio tube is continuous random variable with pdf
`f(x)={{:((100)/x^2","xge100),(0",""else where"):}`
Then, the probability that the life of tube will than 200 h if it is known that th tube is still functioning after 150 h of services is
View Solution
Exercise 2 (MISCELLANEOUS PROBLEMS) questions and complete solutions for chapter PROBABILITY of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12