The probability distribution of the random variable X is given by
Then, the value of V(X) is equal to

A
0
B
1
C
12
D
23
Video Solution
Text Solution
The correct Answer is:B
E(X)=ΣxiP(xi)=18(1)+12(2)+18(3)+14(4)
=18+1+38+1=52
Now, V(X)=E(X2)−[E(X)]2
=Σx2i.P(xi)−(52)2
=18(1)2+12(2)2+18(3)2+14(4)2−254
=18+2+98+4−254
=1+16+9+32−508=58−508=88=1
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - MHT CET Corner4videos
PROBABILITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PROBABILITYEXERCISE - Exercise 1 (TOPICAL PROBLEMS)44videos
PROBABILITY
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - PRACTICE SET 24EXERCISE - Paper 2 (Mathmatics)50videos
PRACTICE SET 24
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEQUENCES AND SERIES EXERCISE - EXERCISE 311videos
SEQUENCES AND SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
The probability distribution of a discrete random variable X is given below

The value of k isA8B16C32D48 - Question 2 - Select One
The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2
The distribution of a random variable X is goven below
The value of k is
 View Solution
View SolutionThe probability distribution of a random variable X is given below
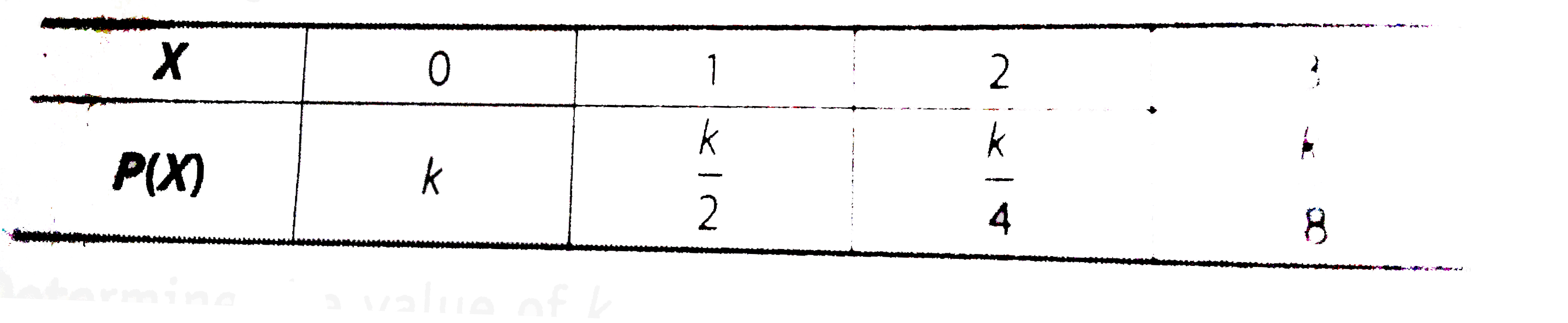
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).View SolutionThe probability distribution of a random variable is as follows: The variance of x is
View SolutionThe probability distribution of a discrete random variable x is given as under

Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.View SolutionIf the probability distribution of a random variable X is as given below
Then, mean and variance are
 View Solution
View SolutionThe probability of a random variable X is given below
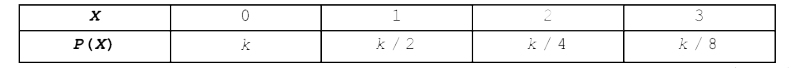
Determine the value of kView Solution



