Complete Solutions to EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method ) of chapter Linear Programming of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | Linear Programming |
| MHTCET PREP GUIDE | EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method ) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Maximum value of Z = 12x + 3y subject to constraints ` x ge 0,y ge 0, x+y le 5 ` and ` 3x+y le 9` is
View SolutionThe coordinate of the point at which minimum value of Z = 7x - 8y, subject to the conditions constraints `x+y - 20 le 0, y ge 5, le -5 ` is
View SolutionThe minimum value of the objective function Z=2x+10y for linear constraints ` x ge 0 , y ge 0, x -y ge 0, x -5y le -5 ` is
View SolutionThe minimum value of Z = 5x - 4y subject to constraints ` x+y le 10 , y le 4, x,y gt 0 ` will be at the point
View SolutionThe maximum value of z = 10x + 6y subject to constraints ` x ge 0, y ge 0, x +y le 12, 2x +y le 20` is
View SolutionThe feasible solution for a LPP is hown as below,

Let Z =3x -4y be the objective function . Then,
Maximum of Z occurs at
View SolutionThe feasible solution for a LPP is hown as below,
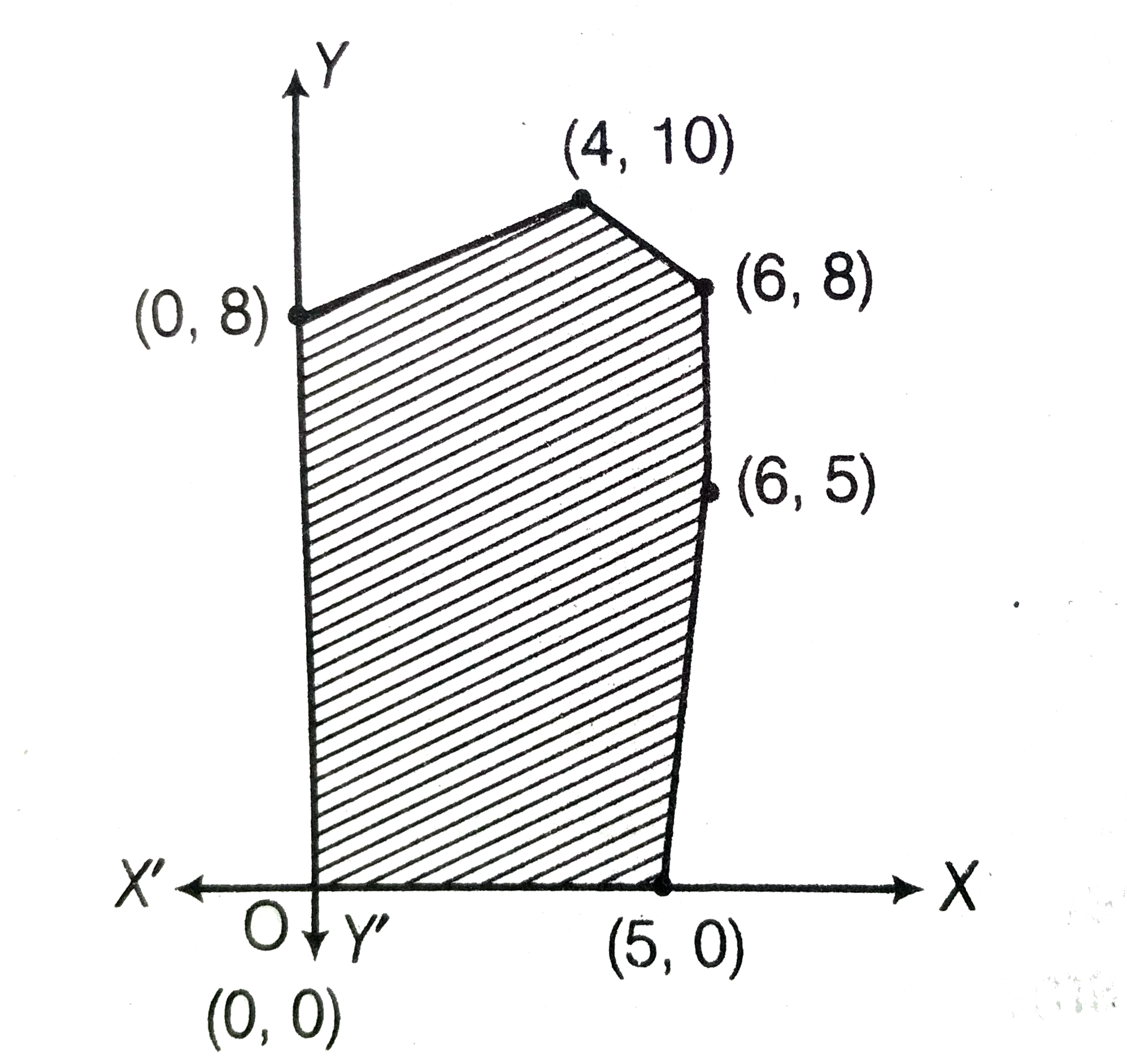
Let Z =3x -4y be the objective function . Then, Minimum of Z occurs at
View SolutionThe feasible solution for a LPP is hown as below,

Let Z =3x -4y be the objective function . Then, (Maximum value of Z + Minimum vlaue of Z) is equal to
View SolutionThe maximum value of Z = 4x + 3y, if the feasible region for an LPP is shown in following figure, is
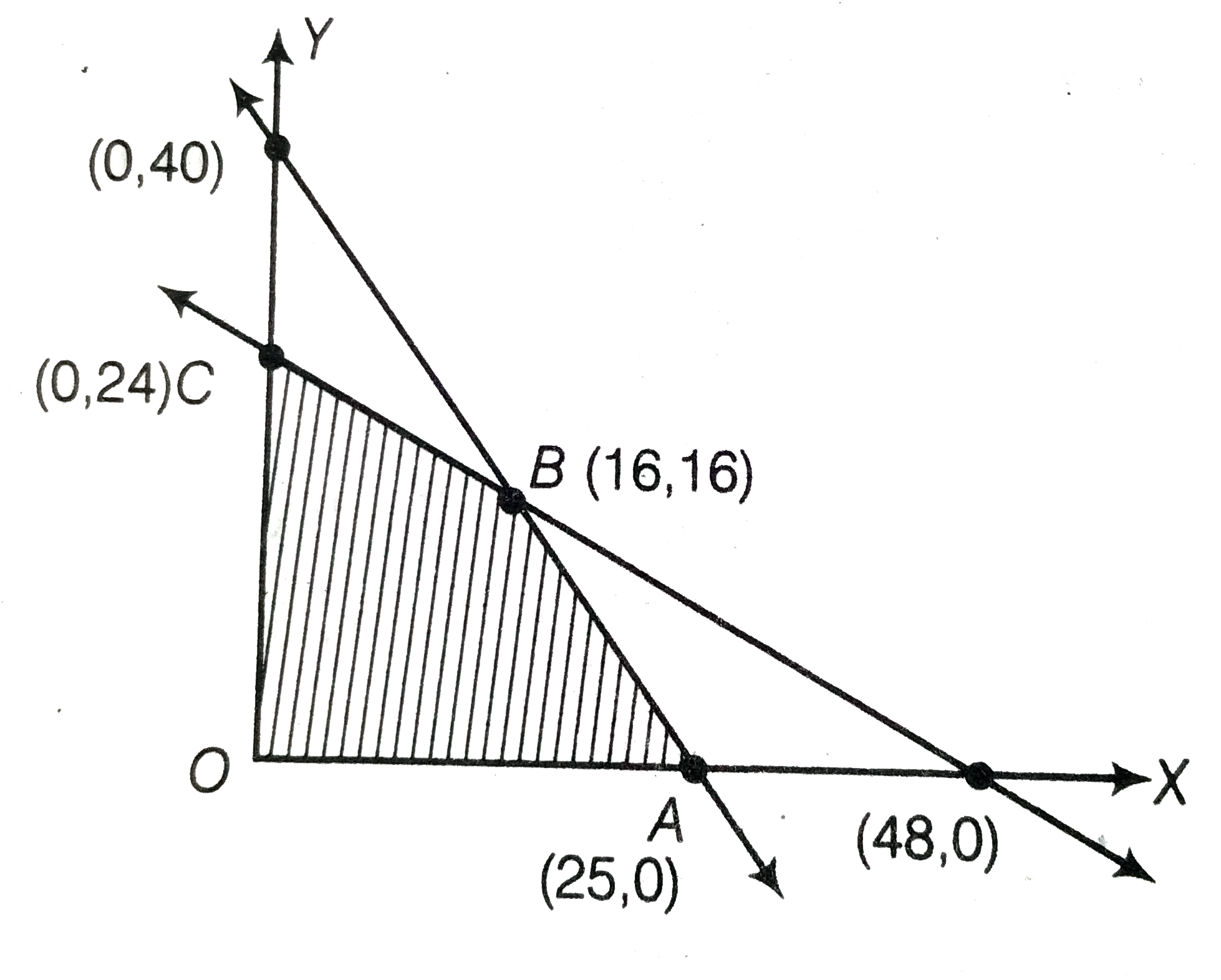
View SolutionThe maximum value of Z =x +3y such that ` 2x +y le 20, x +2y le 20, x ge 0, y ge 0 ` is
View SolutionThe area of the feasible region for the following constraints ` 3y +x ge 3, x ge 0, y ge 0 ` will be
View SolutionThe iinear programming problem Maximise `Z=x_1 +x_2 `
Subject to constraints
` x_1+2x_2 le le 2000`
` x_1+ x_2 le 15000`
` x_2 le 600`
` x_1 ge has `
View SolutionConsider the linear programming problem Maximise Z = 4x + y.
Subject to constraints ` x+y le 50, x +y ge 100` and ` x ,y ge 0 ` Then, maximum vlaue of Z is
View SolutionThe maximum and minimum values of the objective function Z = 3x - 4 y subject to the constraints
`x- 2y le 0, -3x +y le 4 `
` x-y le 6 , x,y ge 0`
are respectively
View SolutionThe maximum value of Z = 4x + 2y subject to the constraints `2x+3y le 18,x+y ge 10, x , y ge 0 ` is
View Solution
EXERCISE 1 (TOPICAL PROBLEMS )(Solution of LPP Graphical Method ) questions and complete solutions for chapter Linear Programming of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12