Complete Solutions to EXERCISE 2 (MISCELLANEOUS PROBLEMS ) of chapter Linear Programming of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | Linear Programming |
| MHTCET PREP GUIDE | EXERCISE 2 (MISCELLANEOUS PROBLEMS ) |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
The point which provides the solution of the linear programming problem, maximise Z = 45x + 55y. Subject to constraints Subject to constraints ` x,y ge 0, 6x +4y le 120` and ` 3x +10 y le 180 ` is
View SolutionDetermine the system of linear equation for which the solution set is the shaded region in the following figure
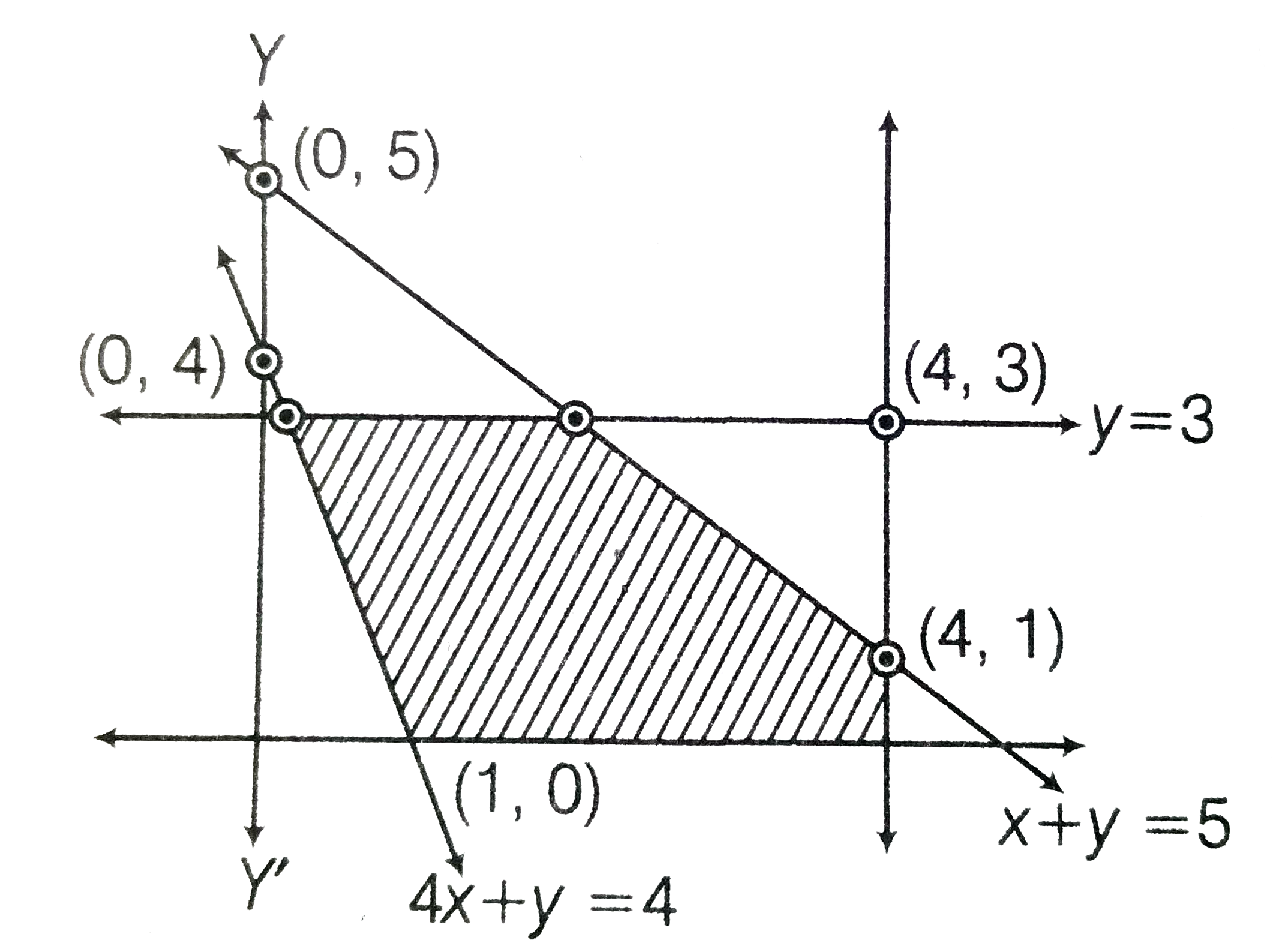
View Solutionif ` x+y le 2,x ge 0 ` then point at which maximum value of 3x + 2y attained will be
View SolutionThe solution set of the linear inequalities `2x + 2y ge 10 ` and ` x+ 2y ge 10`
View SolutionSolve the linear programming problem. Maximise Z = x + 2y
Subject to constraints `x - y le 10, 2x +3y le 20 ` and ` x ge 0, y ge 0 `
View SolutionFor an LPP, minimise Z = 2x + y subject to constraint `5x+10y le 50 , x +y ge 1,y le 4 ` and ` x,y ge 0 ` then Z is equal to
View SolutionConsider the inequalities `x_1+x_2 le 3,2x_1+5x_2ge 10x_1,x_2 ge 0` then feasible region is
View Solution`Z=4x+2y,4x+2y ge 46, x +3y le 24 ` and x and y are greater than or equal to Zero, then the maximum value of Z is
View SolutionThe minimum vlaue ` Z = 2x_1 +3x_2` subject to the conditions `2x_1+7x_2ge22, x_1+x_2ge 6, 5x_1 +x_2 ge 10` and `x_1, x_2 ge 0 ` is
View SolutionThe maximum value `P = 3x + 4y` subjected to the constraints `x + y le 40, x + 2y le 60, x ge 0 and y ge 0` is
View SolutionConsider the inequalities `5x_1+4x_2ge9,x_1+x_2 le 3, x_1 ge 0 , x_2 ge 0` Which of the following point lies inside the solution set ?
View SolutionThe minimum and maximum values problem, of Z for the minimise and maximise Z = 3x + 9 y subject to the constraints
`x+3y le 60,x + y ge 10 , x le y,`
are respectively
View SolutionThe linear programming problem minimiseZ=3x+2y subject to the constraints
`x+y ge 8`
`3x +5y le 15 `
` x ge 0, y ge 0 ` has
View SolutionThe maximum and minimum values of the objective function Z = x + 2y subject to the constraints
` x+2y ge 100, 2x -y le 0, 2x +y le 200` occurs respectively at
View SolutionThe maximum value of the objective function
Z=3x+4y
subject to the constraints ` x+y le 4, x ge 0 , y le o ` is
View SolutionLet x and y are the number of tables and chairs respectively, on which a furniture dealer wants to make profit for the constraints Maximise Z = 250x + 75 y
`5x+y le 100, x +y le 60 x ge 0 y ge 0`
consider the following graph

Then, the maximum profit to the dealer results from buying
View SolutionThe graphical solution of linear inequalities `x+y ge 5 " and " x -y le 3, `
View SolutionBy graphical method, the solutions of linear programming problem maximum ` Z = 3x_1 + 5x_2` subject to constraints `3x_1+2x_2 le 18`
`x_1 le 4, x_2 le 6,x_1 ge 0, x_2 ge 0`
View SolutionA toy company manufactures two types of doll; a basic version doll; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one of type. A and the company would have time to ,make a maximum of 2, 000 per day if it produces only the basic version. The supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined). The deluxe version requires a fancy dress of which there are only 600 per day available. If the company makes profit Rs. 3 and Rs. 5 per doll respectively o doll A and doll B; how many of each should be produced per day in order to maximize profit?
View SolutionThe minimum value of Z = 10x + By subject to ` 4x +y ge 4, x +3y ge 6, x +y ge 3, xge 0, y ge 0` is
View SolutionThe point which provides the solution of the solution to the linear programming problem . Maximum (2x+3y) subject to constraints .
`4x +y ge 4, x +3yge 6,x +y ge 3,x ge 0,y ge 0 ` is
View SolutionShaded region is represented by , the constraints

View SolutionLet R be the feasible region (convex polygon) for a linear programming problem and Z = ax + by be the objective function. Then, which of the following statements is false?
View SolutionThe minimum value of the objective function Z=x+2y
Subject to the constraints,
`2x+ y ge 3 , x +2y ge 6 , x, y ge 0` occurs
View SolutionLet the feasible region of the linear programming problem with the objective function Z = ax + by is unbounded and let M and m be the maximum and minimum value of Z, respectively. Now, consider the following statements
I. M is the maximum value of Z, if the open half plane determined by ax + by gt M has no point in common with the feasible region. Otherwise, Z has no maximum value.
II. mis the minimum value of Z, if the open half plane determined by ax + by lt m has no point in common with the feasible region. Otherwise, Z has no minimum value. Choose the correct option.
View SolutionThe minimum and maximum values of the objective function, Z = 5x + 10y subject to the constraints `x +2yle 120, x+y ge 60, x -2y ge 0 , x,y le 0` are respectively
View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where `p,q gt 0`. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View Solution(Allocation problem) A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profit from crops X and Y per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be
View SolutionAnil wants to invest at the most Rs.12000 in bonds. A and B. According to rules, he has to invest at least Rs.2000 in Bond A is `8%` per annum and on Bond B, it is `10%` per annum, how should he invest his money for maximum interest ? Solve the problem graphically.
View Solution
EXERCISE 2 (MISCELLANEOUS PROBLEMS ) questions and complete solutions for chapter Linear Programming of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12