Complete Solutions to Exercise 1 of chapter FORCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FORCE |
| MHTCET PREP GUIDE | Exercise 1 |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
Which of Newton's laws of motion explain the concept of inertia ?
View SolutionA body of mass 6 kg is acted on a by a force so that its velocity changes from `3 ms^(-1)` to `5ms^(-1)`, then change in momentum is
View SolutionThe momentum p (in kg `ms^(-1)`) of a particle is varying with time t (in second) as `p=2+3 t^(2)`. The force acting on the particle at `t=3s` will be
View SolutionA force `F=(6hati-8hatj+10hatk)`N produces acceleration of `sqrt(2) ms^(-2)` in a body. Calculate the mass of the body.
View SolutionA ball of mass 0.5 kg moving with a velocity of `2 ms^(-1)` strikes a wall normally and bounces back with the same speed. If the time of contact between the ball and the wall is one millisecond, the average force exerted by the wall on the ball is
View SolutionA body of mass 5 kg is moving with velocity of `v=(2hati+6hatj)ms^(-1)` at t=0s. After time t=2s, velocity of body is `(10 hati+6 hatj)`, then change in momentum to body is
View SolutionFind the force exerted by 5 kg block on floor of lift, as shown in figure. `("Take, "g=10 ms^(-2))`

View SolutionThree blocks of masses `m_(1), m_(2)` and `m_(3)` are connected by massesless strings as shown on a frictionaless table. They are pulled with a force `T_(3)=40 N`. If `m_(1)=10 kg, m_(2)=6 kg` and `m_(3)=4` kg, the tension `T_(2)` will be
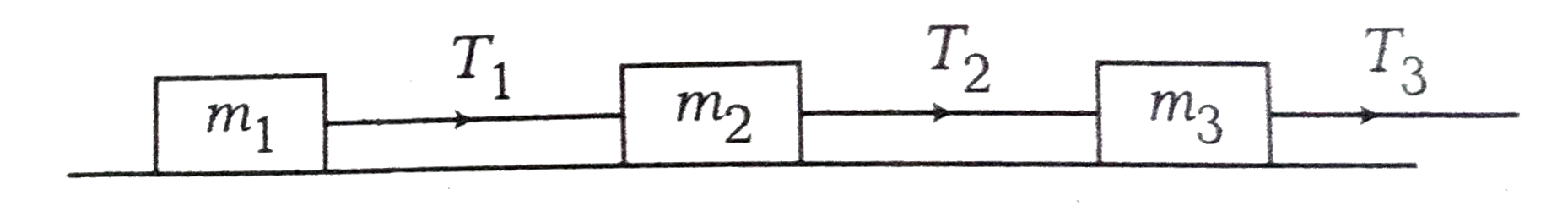
View SolutionThree blocks are placed at rest on a smooth inclined plane with force acting on `m_(1)` parallel to the inclined plane. Find the contact force between `m_(2)` and `m_(3)`.

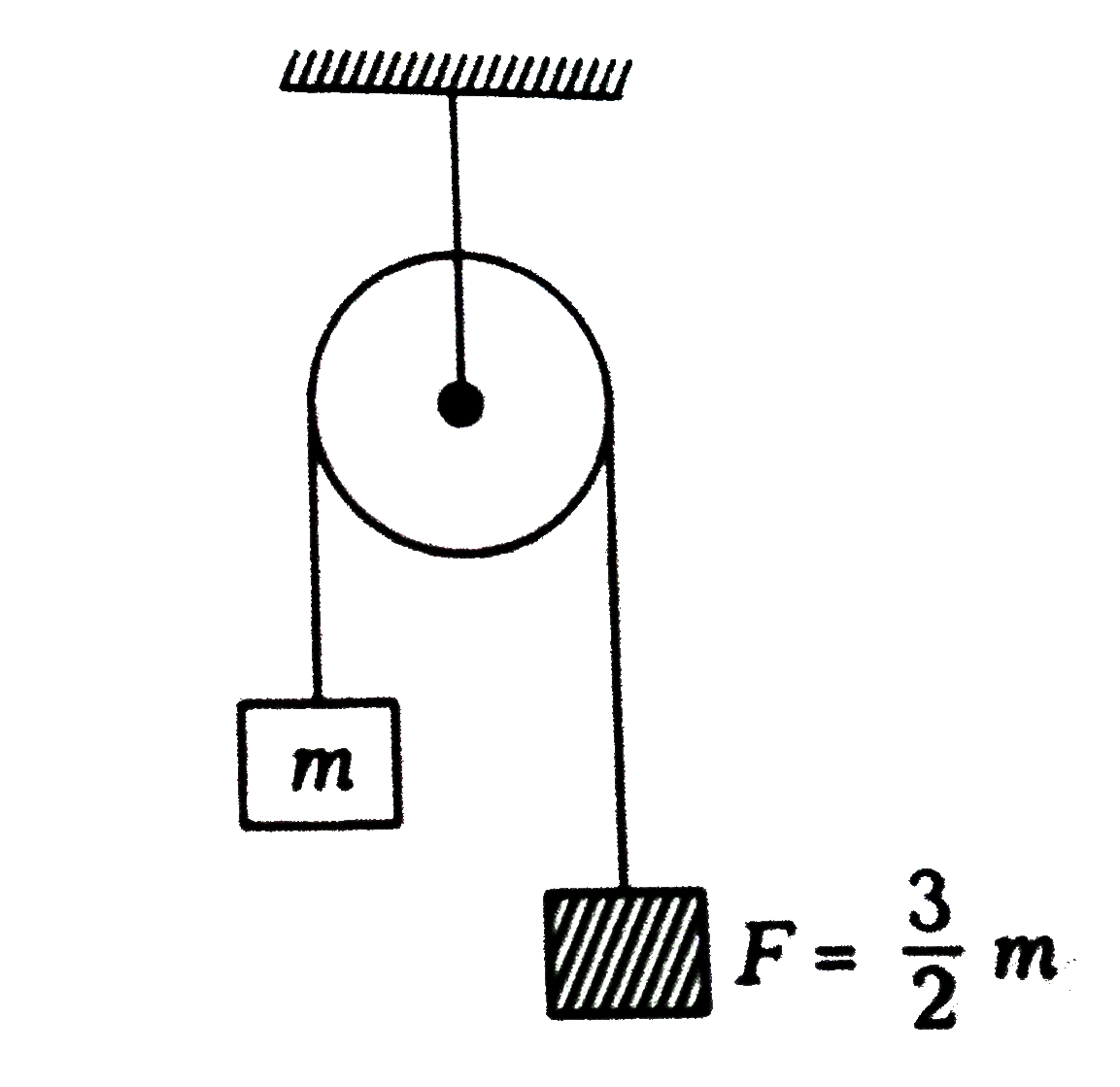
View SolutionIn the arrangement shown, the mass m will ascend with an acceleration (Pulley and rope are massless)
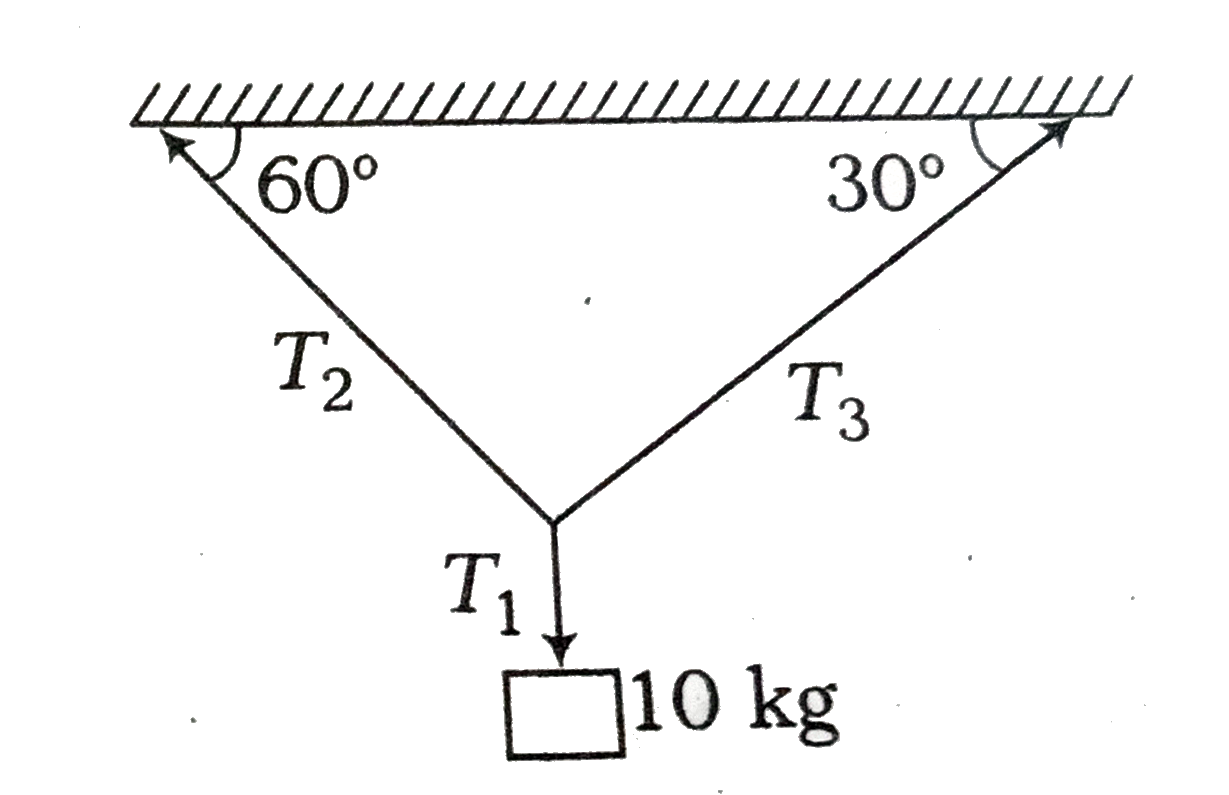
View SolutionA block of mass 10 kg is suspended by three strings as shown in the figure. The tension `T_(2)` is
View SolutionIf impulse I varies time t as I`(kg ms^(-1))=20t^(2)-40t`.
The change in momentum is minimum at :-
View SolutionAn initially stationary device lying on a frictionless floor explodes into two pieces and slides acros the floor. One piece is moving in
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA bullet of mass 0.1 kg is fired with a speed of `100 ms^(-1)`. The mass of gun being 50 kg. Then, the velocity of recoil becomes
View SolutionA gradener pushes a lawn roller through a distance 20 m. If he applies a force of 20 kg-wt in a direction inclined at `60^(@)` to the ground, the work done by him is
View SolutionHow much work must work be done by a force on 50 kg body in order to accelerate it in the direction of force from rest to `20 ms^(-1)` is 10 s?
View SolutionA force `(3 hat(i)+4 hat(j))` acts on a body and displaces it by `(3 hat(i)+4 hat(j))m`. The work done by the force is
View SolutionForce acting on a particale is `(2hat(i)+3hat(j))N`. Work done by this force is zero, when the particle is moved on the line `3y+kx=5`. Here value of k is `(`Work done `W=vec(F).vec(d))`
View SolutionA force `F = Ay^(2)+By+C` acts on a body at rest in the `Y`-direction. The kinetic energy of the body during a displacement `y = -a` to `y = a` is
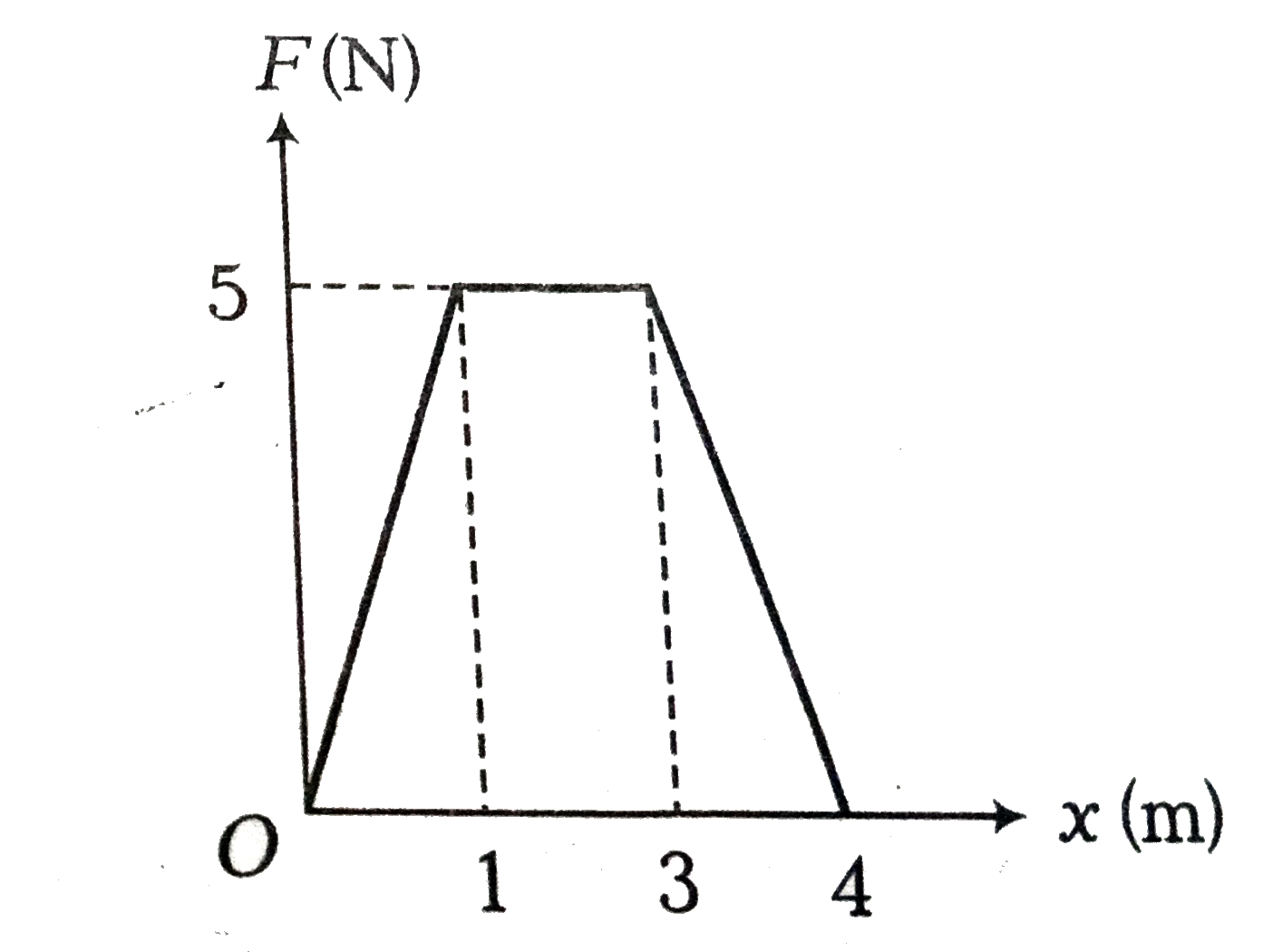
View SolutionThe force F acting on a particle is moving in a straight line as shown in figure. What is the work done by the force on the particle in the 4 m of the trajectory?
View SolutionIf the force acting on a body is inversely proportional to its speed, the kinetic energy of the body is
View SolutionThe kinetic energy acquired by a body of mass m in travelling a certain distance starting from rest, under a constant force is
View SolutionUnder the action of a force, a `2 kg` body moves such that its position x as a function of time is given by `x =(t^(3))/(3)` where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionAn object of mass 5 kg is acted upon by a force that varies with position of the object as shown. If the object starts out from rest at a point `x=0`. What is its speed at `x=50 m`.
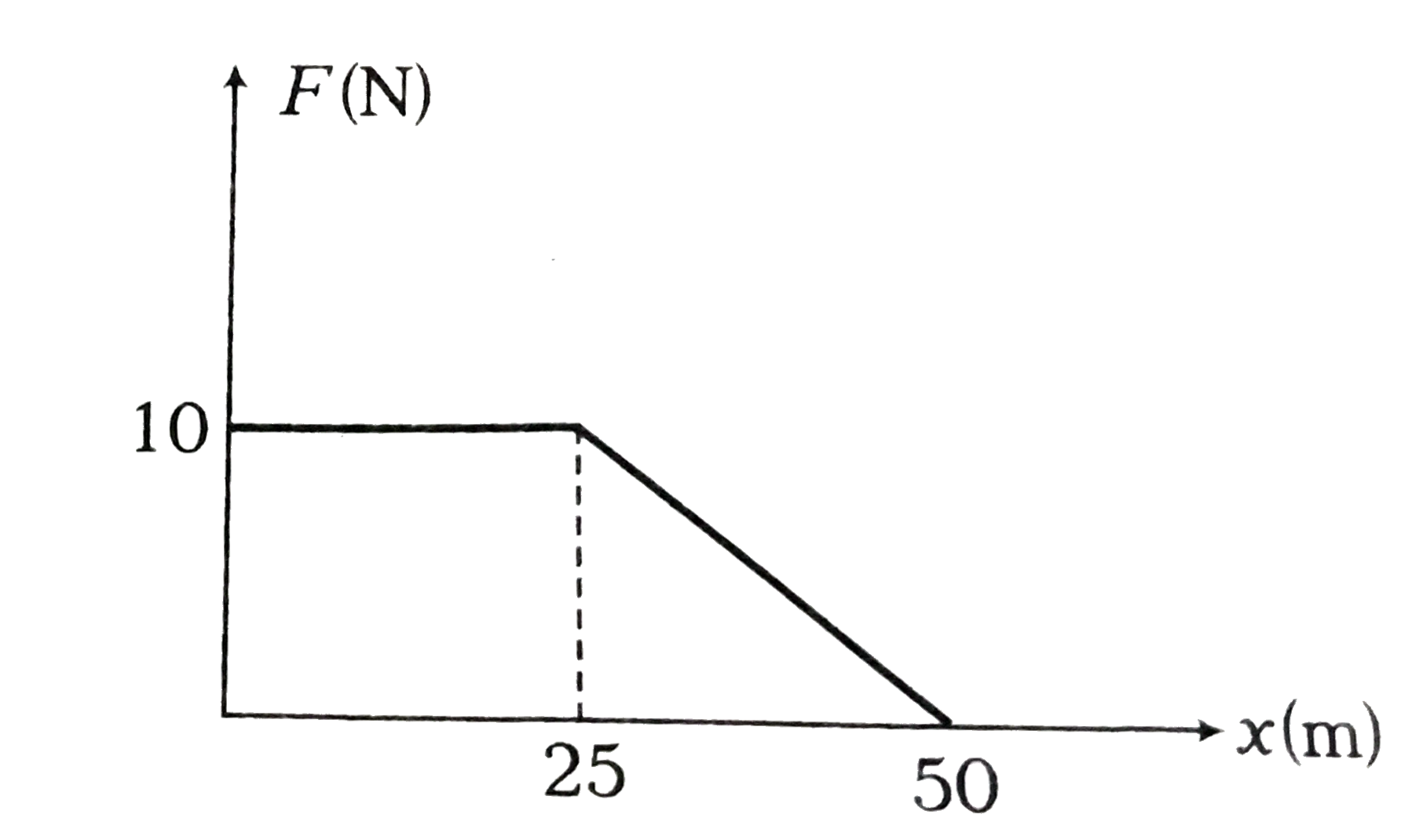
View SolutionA block of mass 20 kg is moving in x-direction with a constant speed of `10 ms^(-1)`. It is subjected to a retarding force `F=(-0.1 x)N` during its travel from `x=20 m` to `x=30m`. Its final kinetic energy will be
View SolutionIn an elastic collison
View SolutionIf a body of mass m collides head on, elastically with velocity u with another identical boday at rest. After collision velocty of the second body will be
View SolutionTwo perfectly elastic particles `A` and `B` of equal masses travelling along a line joining them with velocities `15 m//s` and `10m//s` respectively collide. Their velocities after the elastic collision will be (in m/s) respectively
View SolutionThe collision of two balls of equal mass takes place at the origin of coordinates. Before collision, the components of velocities are (`v_(x) = 50cm^(-1)` , `v_(y) = 0`) and `(v_(x) = -40cm^(-1)` and `v_(y) = 30cms^(-1)`. The first ball comes to rest after collision. The velocity (components `v_(x)` and `v_(y)` respectively) of the second ball are
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA body of mass m moving with velocity v collides head on with another body of mass 2 m which is initially at rest. The ratio of K.E. of colliding body before and after collision will be
View SolutionThe position of centre of mass of system of particles at any moment does not depend on.
View SolutionIn a carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance `1.2xx10^-10m`. The distance of the centre of mass from the carbon atom is
View SolutionTwo bodies of masses 1kg and 2kg are lying in xy plane at (-1,2) and (2,4) respectively. What are the coordinates of the center of mass?
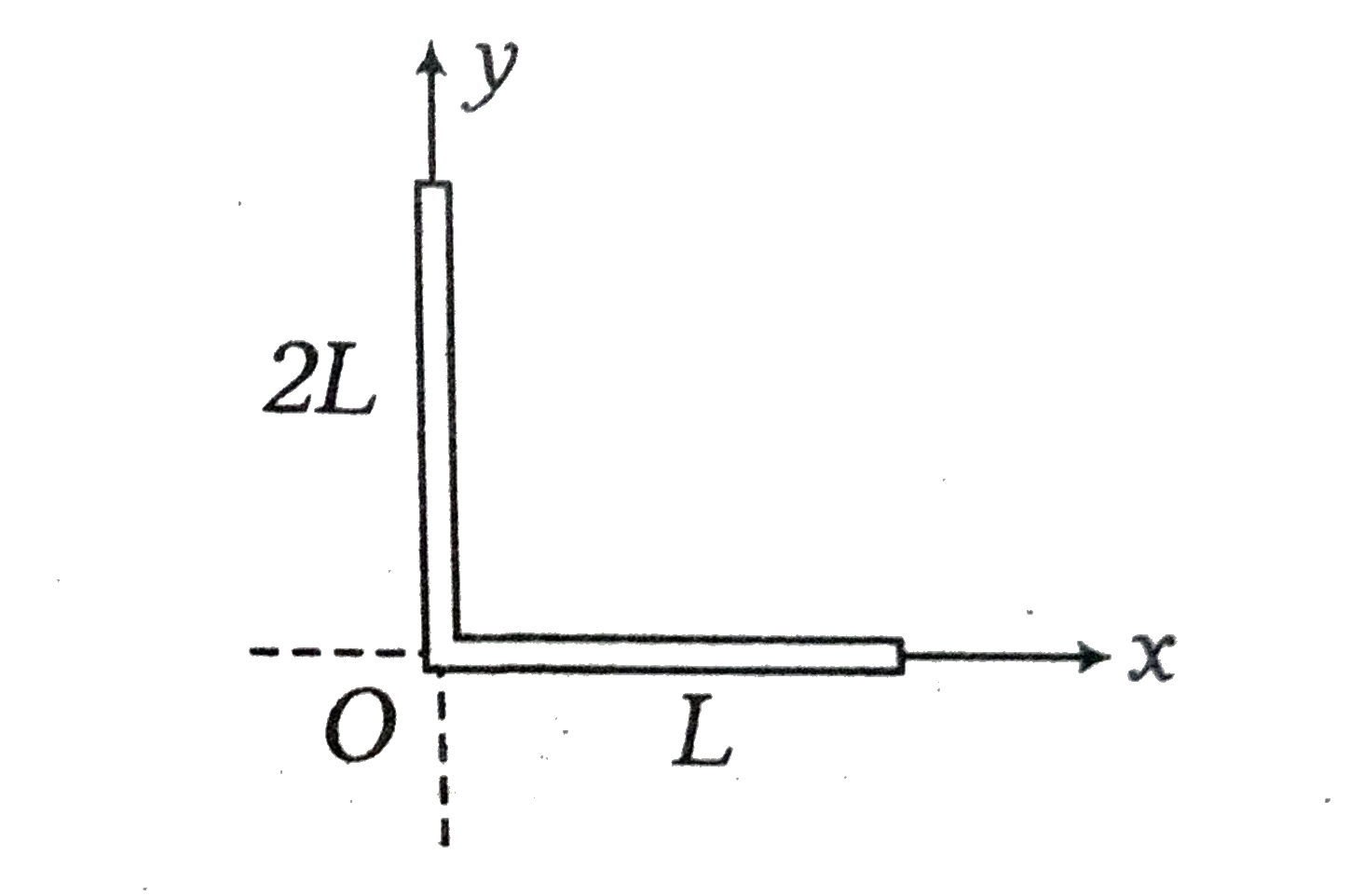
View SolutionFigure shows a composite system of two uniform rods of lengths as indicated. Then the coordinates of the centre of mass of the system of rods are
View SolutionThree point masses `m_(1), m_(2)` and `m_(3)` are placed at the corners of a thin massless rectangular sheet `(1.2 m xx 1m)` as shown. Centre of mass will be located at the point.

View SolutionThe torque of a force `F = - 6 hat (i)` acting at a point `r = 4 hat(j)` about origin will be
View SolutionMoment of a force of megnitude 20 N acting along positive x direction at point (3m 0, 0) about the point (0, 2, 0) (in N-m) is :-
View SolutionThe torque of force `F = -3 hat(i)+hat(j) + 5 hat(k)` acting on a point `r = 7 hat(i) + 3 hat(j) + hat(k)` about origin will be
View SolutionIf angular momentum is conserved in a system whose moment of inertia is decreased, will rotational kinetic energy be conserved.
View Solution
Exercise 1 questions and complete solutions for chapter FORCE of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12