Complete Solutions to EXERCISE 2 (Miscellaneous Problems) of chapter CIRCULAR MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| MHTCET PREP GUIDE | EXERCISE 2 (Miscellaneous Problems) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
A particle is moving on a circular path of 10 m radius. At any instant of time, its speed is `5ms^(-1)` and the speed is increasing at a rate of `2ms^(-2)`. At this instant, the magnitude of the net acceleration will be
View SolutionA vehicle is moving with uniform speed along horizontal, concave and convex surface roads. The surface on which, the normal reaction on the vehicle is maximum is
View SolutionA circular curve of a highway is designed for traffic moving at 72 km/h. if the radius of the curved path is 100 m, the correct angle of banking of the road should be given by:
View SolutionA stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
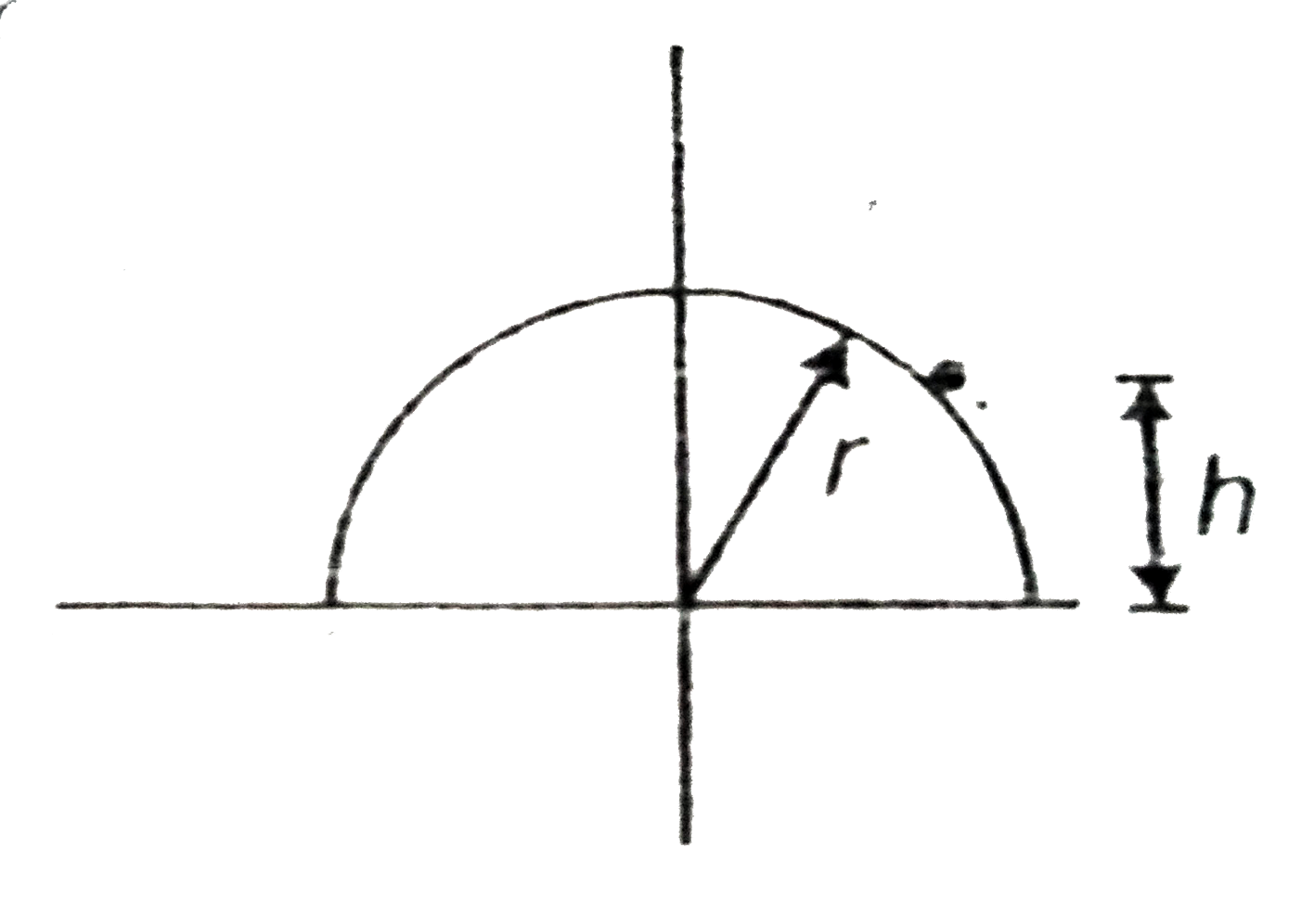
View SolutionA body of mass m hangs at one end of a string of length l, the other and of which is fixed . It is given a horizontal velocity so that the string would just reach where it makes an angle of `30^@` with the vertical . The tension in the string at mean position is
View SolutionA particle is kept at rest at the top of a sphere of diameter 84m. When disturbed slightly ,it slides down .At what height h from the botton , the particle will leaves the sphere
View SolutionA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity `sqrt(7gl//2)`. The string will slack after swinging through an angle equal to
View SolutionA particle moves from rest at a on the surface of a smooth circular cylinder. The equation relating `alpha and beta` is
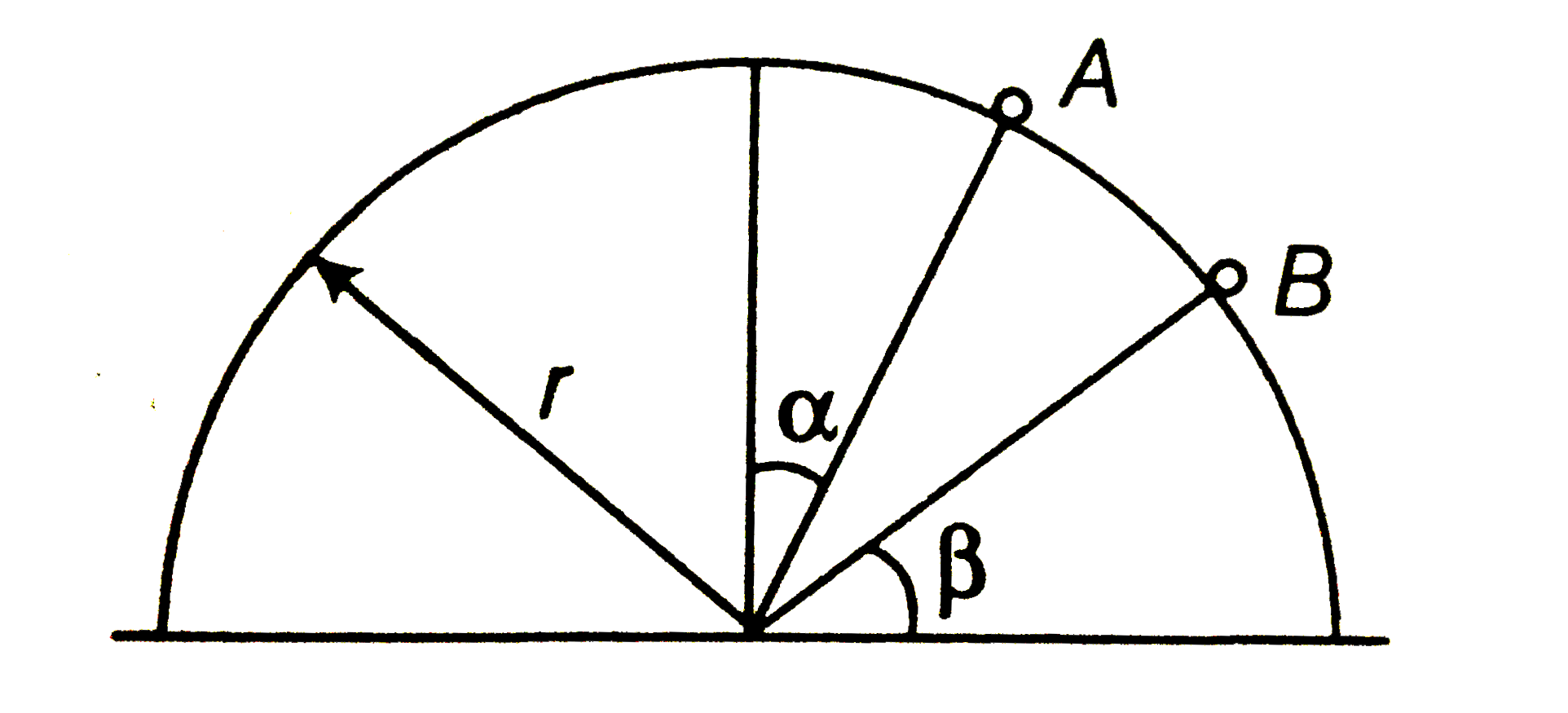
View SolutionA ball suspended by a thread swings ia a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle `theta` of thread deflection in the extreme position will be
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m. The ball is rotated on a horizontal circular path about vertical axis . The maximum tension that the string can bear is 324 N . The maximum possible value of angular velocity of ball (in `rad s^(-1)`)is
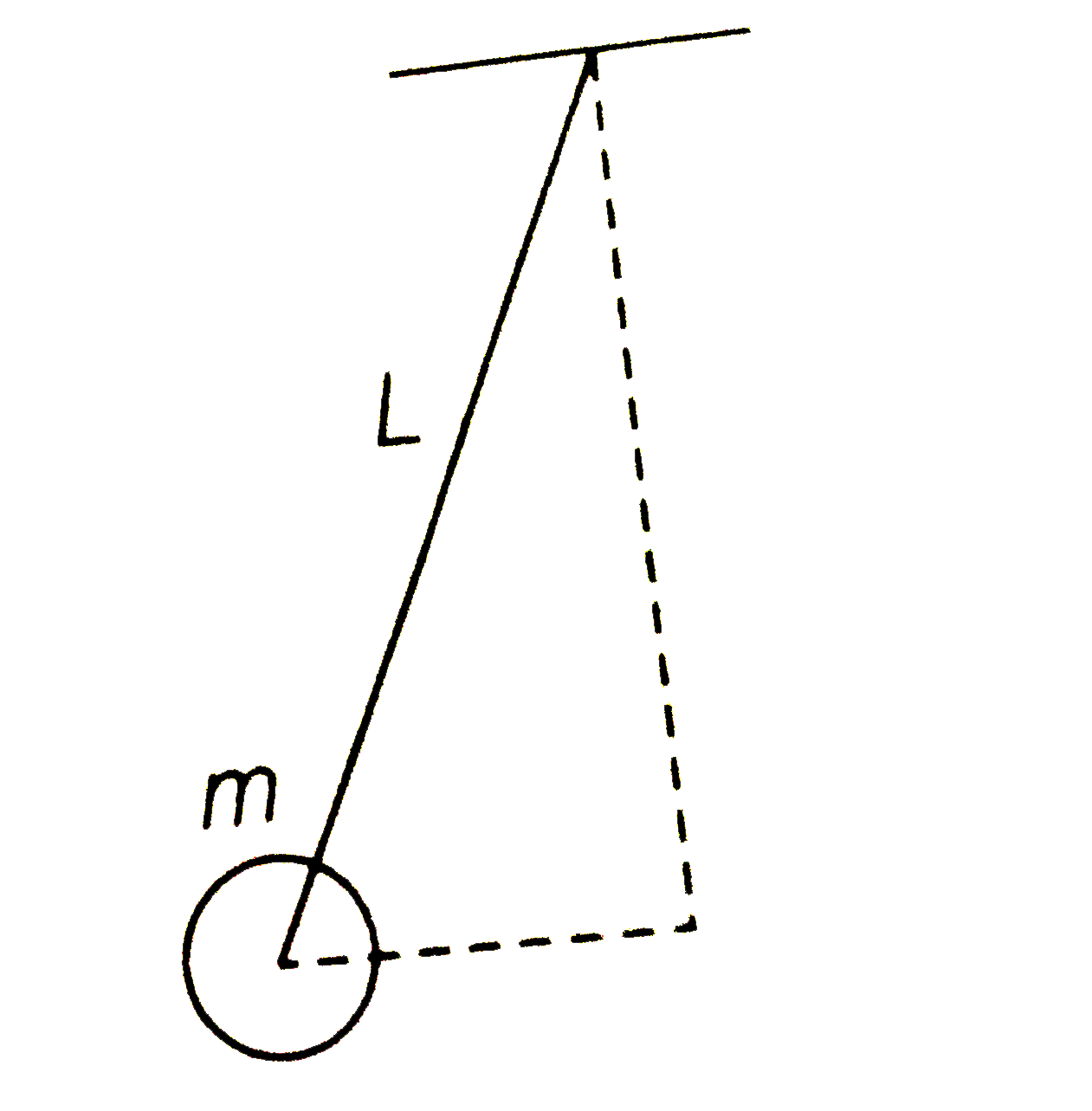
View SolutionA points P moves in counter- clockwise direction on a circular path as shown in the figure . The momement of P is such that it sweeps out a length ` s =t^3+5`, where s is in metre and t is in seconds . The radius of the path is 20 m. The acceleration of P when t =2s is nearly
View SolutionA bob of mass M is suspended by a massless string of length L . The horizontal velocity v at position A is just sufficient to make it reach the points B. The angle `theta `at which the speed of the bob os half of that at A , satisfies

View SolutionThe car of a wheel rotating with centain angular velocity is topped in 5 s and before it stops, it makes 20 revolutions . Then initially it was rotating with the frequency.
View SolutionLength of a simple pendulum is 2m and mass of its bob is 2 kg if the tension in the string exceeds 100 N , it will break . If g =`ms^(-2) `and the bob is whirled in a horizontal plane , the maximum angle through which the sting can make vertical during ratating is
View SolutionA body moving along a circular path of radius R with velocity V , has centripetal acceleration a If its velocity is made equal to 2v , then its centripetal acceleration is
View SolutionA body starts ratating from rest and completes 100 revolutions in 20 s. Find its angular acceleration
View SolutionA weightless thread can bear tension upto 37 N . A stone of mass 500 g is tied to it and revolved in a circular path of radius 4 m in a vertical plane . If g =10`ms^(-2) `, then the maximum angular velocity of the stone will be
View SolutionA small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
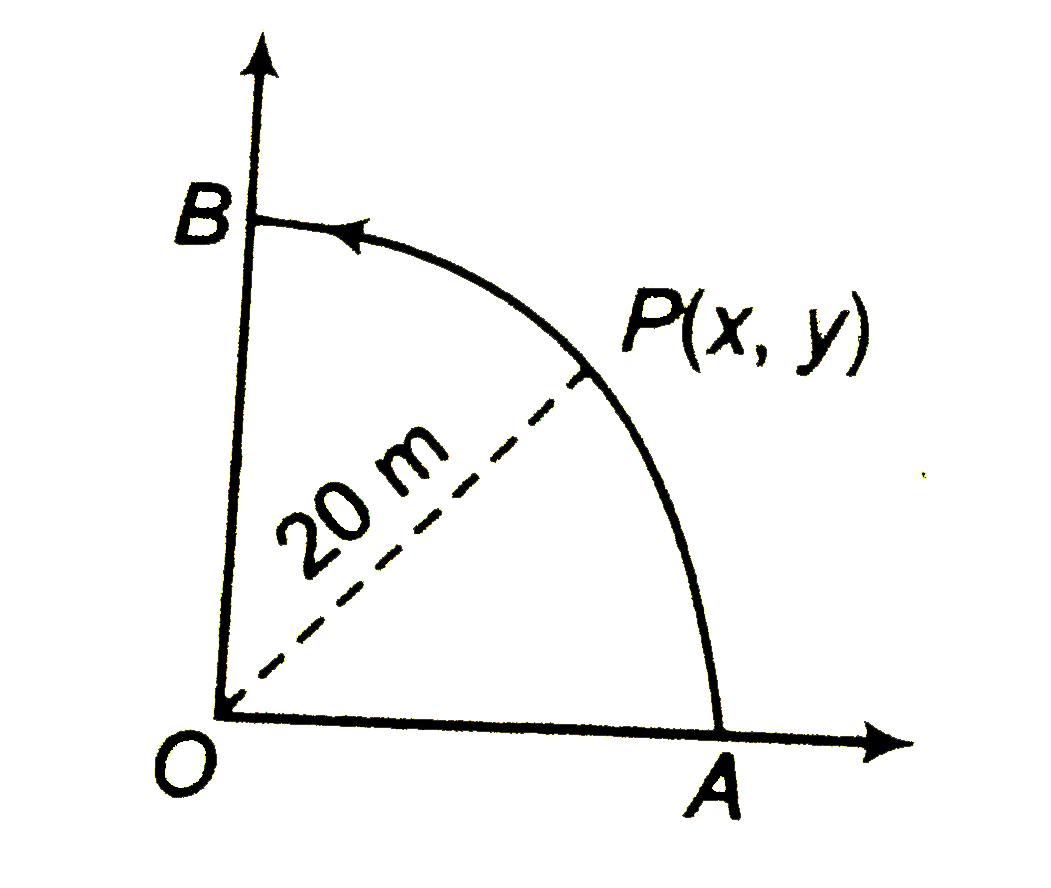
View SolutionThe figure shows a circular path of a moving particle . If the velocity of the particle at some instant is V =-`3hati-4hatj`, through which quadrant is the particle moving when clockwise and anti-clockwise respectively
View SolutionTwo particles A and B start at the origin O and travel in oppsite directions along the circular path at constant speeds `v_A` =0.7 ms and `v_B=1.5 ms^(-1)`, respectively . Determine the time when they collide and the magnitude of the acceleration of B just before this happens .

View SolutionA cyclist is riding with a speed of `27 km h^(-1)`. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate `0.5 ms^(-2)`. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View SolutionYou may have seen in a circus a motorcyclist driving in vertical loops inside a death well (a hollow spherical chamber with holes so the spectators can watch from outside) Explain clearly why the motorcyclist does not drop down when he is at the uppermost point of death well with no support from below What is the minimum speed required at the uppermost position to perfrom a vertical loop if the radius of the chamber is 25 m ?
View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of the acceleration are equal. If its speed at `t = 0` is `u_(0)` the time taken to complete the first revolution is :
View SolutionThe maximum and minimum tension in the string whirling in a circle of radius 2.5 m with constant velocity are in the ratio `5:3` then its velocity is
View Solution
EXERCISE 2 (Miscellaneous Problems) questions and complete solutions for chapter CIRCULAR MOTION of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12