Complete Solutions to Exercise 1 of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| MHTCET PREP GUIDE | Exercise 1 |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
Two speres of radii r and 2r touching each other the force of attraction betweeen them is proportional
View SolutionA solid spere of uniform density and radius R applies a gravitational force of attraction equal to `F_(1)` on a particle placed P distacne 2R from the centre O of the spere A spherical cavity of radius `R//2` is now made in the sphere as shown in the The spere with cavity now applies gravitional force `F_(2)` on same particle placed at P the ratio `F_(2)// F_(1)` will be

View SolutionTwo particles of equal mass `'m'` go around a circle of radius `R` under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance `r_(1)` and farthest away at a distance of `r_(2)`. If `v_(1)` and `v_(2)` are the linear velocities at these points respectively, then the ratio `(v_(1))/(v_(2))` is
View SolutionA acceleration of moon with respect to earth is 0.0027 `ms^-2` and the acceleration of an apple falling on earth's surface is about `10ms^-2`. Assume that the radius of the moon is one fourth of the earth's radius. If the moon is stopped for an instant and then released, it will fall towards the earth. The initial acceleration of the moon toward the earth will be
View SolutionThe accelearation due to gravity on a planet is 1.96 `ms^(-2)` if tit is safe to jump from a height of 3 m on the earth the corresponding height on the planet will be
View SolutionThe mass of the moon is ` (1)/(8)` of the earth but the gravitational pull is ` (1)/(6)` earth It is due to the fact that .
View SolutionImagine a light planet revolving around a very massive star in a circular orbit of radius R with a period of revolution T. if the gravitational force of attraction between the planet and the star is proportational to `R^(-5//2)`, then
(a) `T^(2)` is proportional to `R^(2)`
(b) `T^(2)` is proportional to `R^(7//2)`
(c) `T^(2)` is proportional to `R^(3//3)`
(d) `T^(2)` is proportional to `R^(3.75)`.
View SolutionIf a planet of given density were made larger, its force of attraction for an object on its surface would increase because of the greater distance from the object to the centre of the planet. Which effect predominates?
View SolutionIf radius of earth is R then the height ‘ h ’ at which value of ‘ g ’ becomes one-fourth is
View SolutionThe depth `d`, at which the value of acceleration due to gravity becomes 1/n times the value at the surface is (R = radius of the earth)
View SolutionTwo point masses each equal to 1 kg attract one another with a force of `9.8 ×10^(-9)` kg-wt. the distance between the two point masses is approximately `(G = 6.6 xx 10^(-11) "MKS units")`
View SolutionA body has a weight 72 N. When it is taken to a height `h=R`= radius of earth, it would weight
View SolutionMass `M` is split into two parts `m` and `(M-m)`, which are then separated by a certain distance. What is the ratio of `(m//M)` which maximises the gravitational force between the parts ?
View SolutionTwo astronauts have deserted their spaceship in a region of space far from the gravitational attraction of any other body. Each has a mass of `100 kg` and they are `100 m` apart. They are initially at rest relative to one another. How long will it be before the gravitational attraction brings them `1 cm` closer together?
View SolutionIf there particles, each of mass `M`, are placed at the three corners of an equilateral triangle of side, a the force exerted by this system on another particle of mass `M` placed (i) at the midpoint of side and (ii) at the centre of the triangle are, respectively.
View SolutionIf the diameter of mars is 6760 km and mass one tenth that of the earth the diameter of earth is 12742 km if acceleration due to gravity on earth is `9.8 mx^(-2)` the acceleartion due to gravity on eath is `9.8 m,s^(-2)` the acceleartion due to gravity on mars is
View SolutionA body weighs W newton at the surface of the earth. Its weight at a height equal to half the radius of the earth, will be
View SolutionTwo objects of massses m and 4 m are at rest at infinite separtion they move twoards each other under mutula gravitonal attraction then at a separation r which of the following is true ?
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionTwo particles each of mass M and equidistant from each other move along a circle of radius R under the action of their mutual gravitional attraction the speed of each particle is
View SolutionA body weighs 72 N on the surface of the earth. What is the gravitational force on it due to earth at a height equal to half the radius of the earth from the surface
View SolutionThe change in the value of `g` at a height `h` above the surface of the earth is the same as at a depth d below the surface of earth. When both `d` and `h` are much smaller than the radius of earth, then which one of the following is correct?
View SolutionThe magnitude of gravitational field intensities at distance `r_(1)` and `r_(2)` from the centre of a uniform solid sphere of radius R and mass M are `I_(1)` and `I_(2)` respectively. Find the ratio of `I_(1)//I_(2)` if `r_(1) gt R` and `r_(2) lt R`
View SolutionIf two planets of radii `R_(1) and R_(2)` have densities `d_(1) and d_(2)`, then the ratio of their respective acceleration due to gravity is
View SolutionThe time period of the moon is T= 27.3 days and radius of orbit is `R_(m)=3.84xx10^(8)m` The value of centripetal acceleartion due to earht 's gravity is
View SolutionIf one assume that the gravitational force due to the earth decreases in proportion to the iverse squre of the distance from the centre of the earth then which fo the followng relation between `a_(m) r_(m)` g and `R_(E)`
View SolutionThe force of attraction due to a hollow speheical shell of mass M radius R and and unifor density on a point mass m situdated inside it is
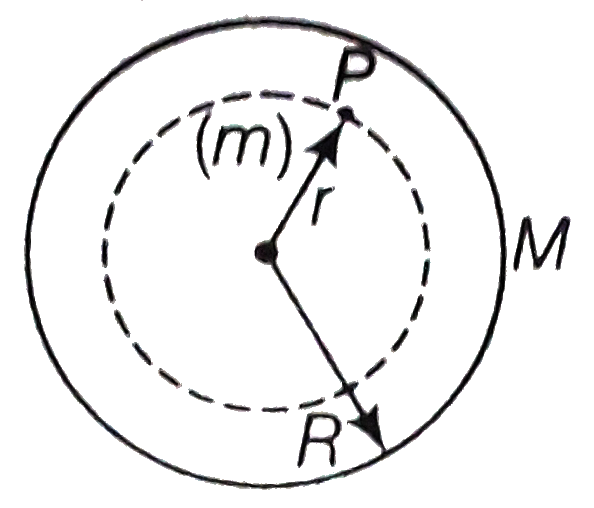
View SolutionThe magnitude of force of attraction on a point mass m due to hollow sperical shell of mass M and radius R as funciton of its distance r form the centre is given is
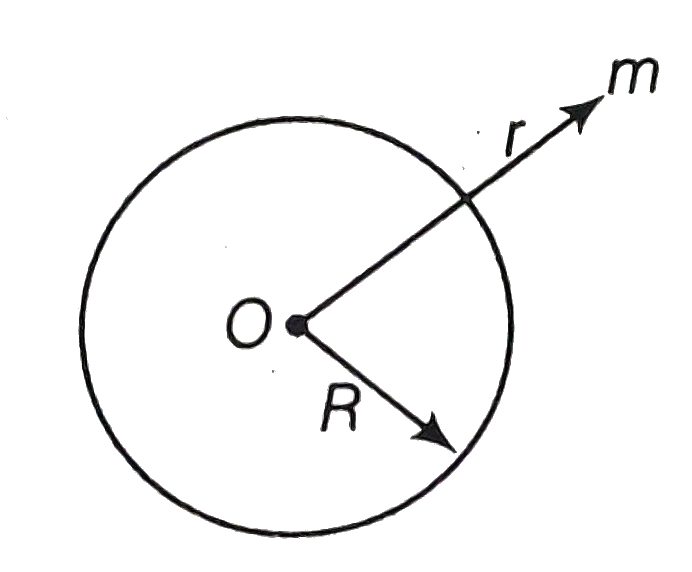
View SolutionIf the radius of earth's orbit is made 1/4, the duration of an year will become
View SolutionThe period of revolution of planet A round from the sun is 8 times that of B. The distance of A from the sun is how many times greater then tht of B from the sun ?
View SolutionWhich of the following graphs between the square of the time period and cube of the distance of the planet from the sun is correct ?
View SolutionA comet of mass m moves in a highly elliptical orbit around the sun of mass M the maximum and minium distacne of the comet from the centre of the sun are `r_(1)` and `r_(2)` respectively the magnitude of angular momentum of the comet with respect to the centre of sun is
View SolutionKepler's third law states that square of period revolution `(T)` of a planet around the sun is proportional to third power of average distance `i` between sun and planet i.e. `T^(2)=Kr^(3)`
here `K` is constant
if the mass of sun and planet are `M` and `m` respectively then as per Newton's law of gravitational the force of alteaction between them is `F=(GMm)/(r^(2))`, here `G` is gravitational constant. The relation between `G` and `K` is described as
View SolutionA staellite in a circular orbit of raidus R has a period of 4h another satellite with orbital radius 3R around the same planet will have a period (in h)
View SolutionThe time period of a satellite of earth is 5 hours. If the separation between the centre of earth and the satellite is increased to 4 times the previous value, the new time period will become-
View SolutionThe ratio of mean distances of three planets from the sun are `0.5 : 1: 1.5`, then the square of time periods are in the ratio of
View SolutionAll planets move in elliptical orbits with the sun situtated at one of the forci of the ellipse the point at wihich the planet is closest to the sun is
View SolutionLaw of areas is valid for any
View SolutionFor motiion of planets in ellipticla orbits around the sun the central force is
View SolutionThe law of areas can be interpreted as
View SolutionKepler 's law of periods as applied to motion of satellite around the earth is givne by
`T^(2)=K(R_(E)+h)^(3)`
Th value of constant is `10^(-13) s^(2) m^(3)` and the Moon is at a distance of `3.84xx10^(5)` km from the earth with reference to hte above reletion and data mathc the items in column I with terms in column II and choose the correct option from the code gives below

View SolutionWhich of the following statement is correct about satellites?
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionA satellite is placed in a circular orbit around the earth at such a height that it always remains sationary with respect to the earth surface in such case it s heights form the earth surface is
View SolutionThe earth (mass `=6xx10^(24)kg`) revolves round the sun with an angular velocity of `2xx10^(-7)"rad/s"` in a circular orbit of radius `1.5xx10^(8)km.` The gravitational force exerted by the sun on the earth, in newtons, is
View SolutionThe orbital velocity of an artifical satellite in a cirular orbit above the earth's surface at a distance equal to radiu of earth is v. For a satellite orbiting at an altitude half of earth's radius, orbital velocity is
View SolutionIf total enrgy of satellite is E what is its potential enrgy
View SolutionA relay satellite transmits the television programme from one part of the world to another part continuously because its period
View SolutionBy what percent the energy of the satellite has to be increased to shift it from an orbit of radius `r` to `(3r)/2`.
View SolutionA satellite moves around the earth in a circular orbit with speed `v`. If `m` is the mass of the satellite, its total energy is
View SolutionThe field which artifical satellite are useful stelites are useful for practical purpose is
View SolutionA lauching vehicle carrying an artificial satellite of mass `m` is set for launch on the surface of the earth of mass `M` and radius `R`. If the satellite intended to move in a circular orbit of radius `7R`, the minimum energy required to be spent by the launching vehicle on the satellite is
View SolutionA body is orbiting around earth at a mean radius which is two times as greater as the parking orbit of a satellite, the period of body is
View SolutionThe time period of an earth satellite in circular orbit is independent of
View SolutionThe radius of the orbit of a satellite is r and its kinetic energy is k if the radius of the orbit is doubled then the new kinetic energy k is
View SolutionThe pitentil energy of a satellite is given as
`PE= lambda(KE)`
where PE = potential energy of the satellite
KE = kinetic energy of the satellite
The vlaue of constant `lambda` is
View SolutionA 400 kg satellite is in a circular orbit of radius 2 `R_(E)` about the earth where `R_(E)`= radius of the earth with reference to the above situation match the term in column I with items in column II and choose the correct option from the codes given below

View SolutionThe time period of a geostationary satellite at a height 36000 km is 24 h a spy satellite orbits vergy close to earth surface (R=6400 km ) what will be its time period ?
View SolutionA simple pendulum has a time period `T_(1)` on the earth 's surface and `T_(2)` when taken to height 2R above the earth 's surface when R is 2R above earth 'ssurface where R is the radius of earht The value of `(T_(1)// T_(2))`
View SolutionThe mass of a planet is six times that of the earth. The radius of the planet is twice that of the earth. It's the escape velocity from the earth is `v`, then the escape velocity from the planet is:
View SolutionFor a body to escape from earth, angle from horizontal at which it should be fired is
View SolutionThe escape velocity form the earth is 11 `kms^(-1)` the esacpe velocity from a planet having twice the radius and the same mean denisty as the earth would be
View SolutionThe ratio of the radii of the planets `P_(1)` and `P_(2)` is a the ratio of their acceleraton due to gravity is b the ratio of the escape velocity form them will be
View SolutionThe mass of the moon is `7//81` th of earth 's mass and its radius is `1//4` th that of the earth if the escape velocity from the earth surface is 11.2 `kms^(-1)` its value for the moon will be
View SolutionThe escape velocity of a body from the earth is `V_(e)` if the radius of earth contracts to `1//4` th of its value keeping the mass of the earth constant the escape velocity will be
View SolutionWhat is the escape velocity for body on the surface of planet on which the accelearation due to gravity is `(3.1)^(2)ms^(2)` and whose radius is 8100 km ?
View SolutionWhat is a period of revolution of the earth satellite ? Ignore the height of satellite above the surface of the earth.
Given,
(i) the value of gravitational acceleration, `g = 10 ms^(-2)`
(ii) radius of the earth, `R_(g) =6400` km (take, `pi = 3.14`)
View SolutionTwo spherical planets P and Q have the same uniform density `rho,` masses `M_p and M_Q` and surface areas A and 4A respectively. A spherical planet R also has uniform density `rho` and its mass is `(M_P + M_Q).` The escape velocities from the plantes P,Q and R are `V_P V_Q and V_R` respectively. Then
View Solution
Exercise 1 questions and complete solutions for chapter GRAVITATION of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12