Complete Solutions to Exercise 2 of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| MHTCET PREP GUIDE | Exercise 2 |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
If the radius of the Earth shrinks by `2%`, mass remaing same, then how would the have of acceleration due to gravity change?
View SolutionAt what height, the weight of the body is same as that at same depth from the earth's surface (take, earth's radius = R)
View SolutionIf the radius of the earth were to shrink by 1% its mass remaining the same, the acceleration due to gravity on the earth's surface would
View SolutionTow spherical planet A and B have same mass but of acceleartion due to gravity at the surface of A to its value at surface of B is
View Solution320 Km above the surface of earth the value of acceleartion due to gravity is nearly 90% of ts value on the sruface fo the earth its value will be 95 % of the value on the eath surface
View SolutionThe acceleration due to gravity at a height `(1//20)^(th)` the radius of the earth above earth s surface is `9m//s^(2)` Find out its approximate value at a point at an equal distance below the surface of the earth .
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass `m` is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass `m` is
View SolutionThree indentical bodes of mass M are locatd at the verticles of an equailateral triangle of side L they revolve undr the effect of mutual gravitational force in a circular orbit circumscibing the traingle while preserving the equilateral triangle their orbital velocity is
View SolutionFrom a solid spere of mass M and radius R a sperhical poriton of radius `(R )/(2)` is removed as show in the taking gravitational potential V=0 at `r= infty` the potential at the centre of the cavity thus formed (G= gravitonal constant )
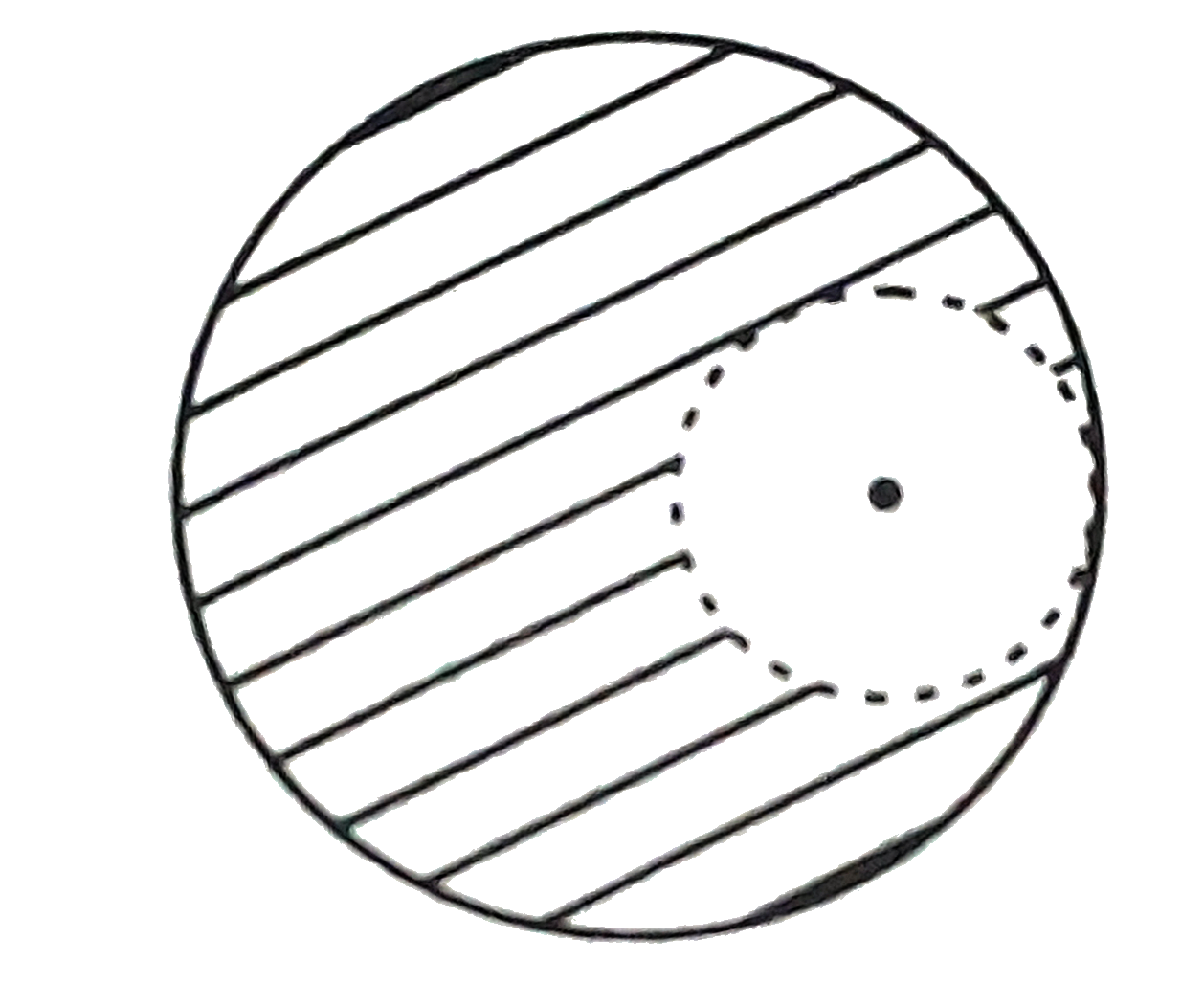
View SolutionThe ratio of radii of earth to another planet is `2//3` and the ratio of their mean densities is `4//5` if an astronaut can jump to a maximum height of 1.5 m on the earth with the same effort the maximum height he can jump on that planet is
View SolutionThe height at which the acceleration due to gravity becomes `g//9` in terms of R the radius of the earth is
View SolutionThe effect of rotation of the eath on the value of acceleration deu to gravity g is
View SolutionA rocket is launched vertical from the surface of the earth of radius R with an initial speed `v`. If atmospheric resistance is neglected, then maximum height attained by the rocket is
View SolutionSuppose the gravitational force varies inversely as then n th power of distance then the time period of a planet in circular orbit of radius r around the sun will be propotinal to
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If `R` is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionPertaining to two planets, the ratio of escape velocities from respective surfaces is `1:2` , the ratio of the time period of the same simple pendulum at their respective surfaces is `2:1` (in same order). Then the ratio of their average densities is
View SolutionFour equal masses (each of mass M) are placed at the corners of a squares side a the escape velocity of a body from the centre O of the square is
View SolutionA point `P(Rsqrt(3),0,0)` lies on the axis of ring of mass M and radius R the ring is located in YZ plane with its centre at origin O A small particle of mass m starts from P and reaches O under gravitatinal attracton only its speed at O will be
View SolutionThe ratio of energy required to raise a satellite to a height `h` above the earth surface to that required to put it into the orbit is
View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
View SolutionThe magnitude of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `F_(1)` and `F_(2)` respectively. Then:
View SolutionA satellite is revolving round the earth with orbital speed `v_(0)` if it is imagined to stop suddenly the speed with which it will strike the surface of the earth would be `(v_(e)` - escape speed of a body from earth s surface)
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionSuppose a verticle tunnel is alng the diametrer of earth assumed to be a sphere of uniform mass density p if a body of mass m is thrown in this tunnel its acceleration at a distance y from the centre is given by

View SolutionF is the gravitational force between two point masses `m_(1)` and `m_(2)` , separated by a distance d. A point mass `2m_(1)` is then brought near `m_(1)`. What is the total force on `m_(2)` ?
View SolutionA planet of mass `m` moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are `r_(1)` and `r_(2)`, respectively. Find the relation between the time period of the planet in terms of `r_(1)` and `r_(2)`.
View SolutionAn artifical satellite of mass 'm' is moving in a circular orbit aroundthe earth. The height of the satellite above the surface of the earth is R. Suppose that it stops suddenly in its orbit and falls freely under gravity. With what speed it will strike the surface of the earth?
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of esacpe velocity from the earth the height of the satellite satellite above the earth surface will be
View SolutionThe period of a planet around sun is 27 times that of earth the ratio of radius of planet orbit to the radius of earth's orbit is
View SolutionThe satellite of mass m revolving in a circular orbit of radius r around the earth has kinetic energy E. then, its angular momentum will be
View SolutionWhich of the following most closely depicts the correct variation of the gravitational potential V(r ) due to a large planet of radius R and unifrom mass denisty ?
View SolutionThere are two particles of masses `m_(1)` and `m_(2)` separted by a distance 'r'
with reference to the above situtation match the item in column II with terms in column II and choose the options from the codes given below

View SolutionIf the big sphere and the small are of masses M,m respectively and d is the separation between their centres then the grvitational force is F if the mass of the big shpere is doubled the restoring torque at equilibrium is
View SolutionIf the distance between the sun and the earth is increased by three times, then attraction between two will
View SolutionDependence of intensity of gravitational field `(E)` of earth with distance `(r)` from centre of earth is correctly represented by
View SolutionA body of mass `m` taken form the earth's surface to the height is equal to twice the radius `(R)` of the earth. The change in potential energy of body will be
View Solution
Exercise 2 questions and complete solutions for chapter GRAVITATION of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12