Complete Solutions to EXERCISE 1 of chapter STATIONARY WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | STATIONARY WAVES |
| MHTCET PREP GUIDE | EXERCISE 1 |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
When a string is divided into three segments of lengths `l_(1),l_(2) and l_(3)` the fundamental frequencies of these three segments are `v_(1), v_(2) and v_(3)` respectively. The original fundamental frequency (v) of the string is
View SolutionTwo pulses having equal and opposite displacements moving in oppositee directions overlap at `t = t_(1)` sec. The resultant displacement of the wave at `t=t_(1)` sec is
View SolutionA uniform wire of linear density 0.004 per kg-m, when stretched between two rigid supports, with a tension `3.6 xx 10^(2)` N, resonates with a frequency of 420 hz. The next harmonic frequency with which the wire resonates is 490 Hz. The length of the wire in metre is
View SolutionA string is hanging from a rigid support. A transverse pulse is excited at its free end. The speed at which the pulse travels a distance x is proportional to
View SolutionA metal wire of linear mass density of `9.8g//m` is stretched with a tension of `10 kg-wt` between two rigid support `1meter` apart. The wire passes at its middle point between the poles of a permanent magnet, and it vibrates in resonance when carrying an alternating current of frequency `n`. the frequency `n` of the alternating source is
View SolutionA uniform string of length `1.5` m has two successive harmonics of frequencies 70 Hz and 84 Hz. The speed of the wave in the string (in `ms^(-1)`) is
View SolutionA uniform rope of mass `0.1` kg and length `2.5` m hangs from ceiling. The speed of transverse wave in the rope at upper end at a point `0.5` m distance from lower end will be
View SolutionA string of mass 2.50kg is under a tension os 200N. The length of the stretched string is 20.0m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
View SolutionThe equation of a stationary wave along a stretched string is given by `y = 4 sin frac{2pi"x"}{3} cos 4Opit` where, x and y are in cms and t is in sec. The separation between two adjacent nodes is
View SolutionThe wave generated from up and down jerk given to the string or by up and down motion of the piston at the end of the pipe is
View SolutionA wave frequency `100 Hz` travels along a string towards its fixed end . When this wave travels back after reflection , a node is formed at a distance of `10 cm `from the fixed end . The speed of the wave (incident and reflected) is
View SolutionThe equation of a stationary wave on a string clamped at both ends and vibrating in its third harmonic is given by `y=0.5 sin (0.314"x") cos (600pit)` where x and y are in cm and t is in sec. What is the length of the string?
View SolutionFor a stationary wave, `t = 8 sin ((pix)/(20)) cos (50 pit)`. What is the distance between two successive antinode ?
View SolutionTwo instruments having stretched strings are being played in unison . When the tension in one of the instruments is increases by ` 1% , 3` beats are produced in ` 2 s`. The initial frequency of vibration of each wire is
View SolutionA string vibrates with a frequency of 200Hz. Its length is doubled and its tension is altered till it begins to vibrate with a frequency of 300Hz. What is the ratio of new tension to the original tension ?
View SolutionThe speed of a wave on a string is 150 `"ms"^(-1)` when the tension is 120 N. The percentage increase in the tension in order to raise the wave speed by `20%` is
View SolutionA string has tension T. For tripling the frequency. The tension is string will become
View SolutionA string of length `0.4 m` and mass `10^(-2)kg` is tightly clamped at its ends. The tension in the string is `1.6 N`. Identical wave pulse are produced at one end at equal intervals of time, `Deltat`. The minimum value of `Deltat` which allows constructive interference of successive pulse is
View SolutionA wave of length `2m` is superimposed on its reflected wave to form a stationary wave. A node is located at `x=3m`, the next node will be located at `x` equals to
View SolutionEquation of a plane progressive wave is given by `y=0.6 sin 2pi(t-(x)/(2)).` On reflection from a denser medium, its amplitude becomes `2//3` of the amplitude of the incident wave. The equation of the reflected wave is
View SolutionTwo uniform strings `A and B` made of steel are made to vibrate under the same tension. If the first overtone of `A` is equal to the second overtone of `B` and if the radius of `A` is twice that of `B`, the ratio of the lengths of the strings is
View SolutionA string of mass 0.2 kg/m and length l= 0.6 m is fixed at both ends and streteched such that it has a tension of 80 N. the string vibrates in 3 segments with maximum amplitude of 0.5 cm. the maximum transevers velcotiy amplitude is
View SolutionA stretched string of length l, fixed at both ends can sustain stationary waves of wavelength `lambda` given by
View SolutionTwo strings of the same material and the same area of cross-section are used in an wxperiment. One is loaded with 12 kg and the other with 3 kg The fundamental fequency of the first string is equal to the first overtone of the second string. If the length of the second string is 100 cm, then the length of the first string is
View SolutionA segment of wire vibrates with fundamental frequency of 40 Hz under a tension of 9 kg-wt. Then, tension at which the fundamental frequency of the same wire becomes 900 Hz is
View SolutionThe equation of stationary wave along a stretched string is given by `y=5 sin ((pix)/(3)) cos 40 pi t `, where x and y are in cm and t in second. The separation between two adjacent nodes is
View SolutionThe temperature at which the speed of sound in air becomes double its value at `0^(@) C` is
View SolutionA stretched wire of lenth 110 cm is divided into three segments whose frequencies are in ratio `1 : 2 : 3.` Their length must be
View SolutionThe tension in a wire is decreased by `19%` the percentage decrease in frequency will be
View SolutionTwo vibrating strings of the same material but lengths `L` and `2L` have radii `2r` and `r` respectively. They are stretched under the same tension. Both the string vibrate in their fundamental nodes, the one of length `L` with freuqency `v_(1)` and the other with frequency `v_(2)`. the ratio `v_(1)//v_(2)` is given by
View SolutionA string in a musical instrument is 50 cm long and its fundamental frequency is 800 Hz. If a frequency of 1000 Hz is to be produced, then required length of string is
View SolutionA wave representing by the equation `y = a cos(kx - omegat)` is suerposed with another wave to form a stationary wave such that point `x = 0` is a node. The equation for the other wave is
View SolutionTwo stratched strings of same material are vibrating under some tension in fundamental mode. The ratio of their froquencies is ` 1 : 2` and ratio of the length of the vibrating segments is ` 1: 4` Then, the ratio of the radii of the strings is
View SolutionA uniform wire of length `L`, diameter `D` and density `rho` is stretched under a tension `T`. The correct relation between its fundamental frequency `f`, the length `L` and the diameter `D` is
View SolutionTo increase the frequency by `20%`, the tension in the string vibrating on a sonometer has to be increased by
View Solutionthe frequency of a sonometer wire is 10 Hz. When the weight producing th tensions are completely immersed in water the frequency becomes 80 Hz and on immersing the weight in a certain liquid the frequency becomes 60 Hz. The specific gravity of the liquid is
View SolutionWhen the length of the vibrating segment of a sonometer wire is increased by `1%` the percentage change in its frequency is
View SolutionTwo forks A and B when sounded together produce four beats `s^(-1)`. The fork A is in unison with 30 cm length of a sonometer wire and B is in unison with 25 cm length of the same wire at the same tension. The frequencies of the forks are
View SolutionA pipe of 60 cm long and open at both the ends produces harmonics. Which harmonic mode of pipe resonates a `2.2` kHz source? Given, speed of sound in ari ` = 300 ms^(-1)`.
View SolutionIf we study the vibration of a pipe open at both ends, then the following statements is not true
View SolutionTwo organ pipes, each closed at one end, give 5 beats `s^(-1)` when emitting their fundamental notes. If their lengths are in the ratio `50 : 51, ` their fundamental frequencies are
View SolutionThe frequency of the first overtons of a closed pipe of length `l_(1)` is equal to that of the first overtone of an open pipe of length `l_(2)` The ratio of their lengths `l_(1) : l_(2)` is
View SolutionAir is blown at the mouth of an open tube of length 25 cm and diameter 2 cm. If the velocity of sound in air is `330 ms^(-1)`, then the emitted frequencies (in Hz) are
View SolutionA pipe opened at both ends prpduces a note of frequency `f_(1)`. When the pipe is kept with `3/4th` of its length in water, it produces a note of frequency `f_(2)`. The ratio `f_(1)/f_(2)` is
View SolutionA closed organ pipe of length 1.2 m vibrates in its first overtone mode. The pressure variation is maximum at
View SolutionAn organ pipe P closed at one end vibrates in its first narmonic. Another organ pipe Q open at both ends vibrates in its third harmonic. When both are in resonance with a tuning fork, the ratio of the length of P to that of Q is
View SolutionTwo closed organ pipe A and B have the same length. A is wider than B. They resonate in the fundamental mode at frequencies `V_(A) and V_(B)` respectively , then
View SolutionIf `lambda_(1), lambda_(2), lambda_(3)` are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths `lambda_(1) : lambda_(2) : lambda_(3)`, is :
View SolutionAn organ pipe is closed at one end has fundamental frequency of 1500 Hz. The maximum number of overtones generated by this pipe which a normal person can hear is
View SolutionTwo closed organ pipes of length 100 cm and 101 cm 16 beats is 20 sec. When each pipe is sounded in its fundamental mode calculate the velocity of sound `
View SolutionAn open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is found to be higher by `100 Hz` then the fundamental frequency of the open pipe. The fundamental frequency of the open pipe is
View SolutionAn open organ pipe has fundamental frequency 100 Hz. What frequency will be produced if its one end is closed ?
View SolutionA pipe closed at one end open at the other end, resonates with sound waves of frequency 135 Hz and also 165 Hz, but not with any wave of frequency intermediate between these two. Then, the frequency of the fundamental note is
View SolutionA glass tube is open at both the ends. A tuning fork of frequency f resonates with the air column inside the tude. Now, the tube is placed bertically inside water so that half the length of the tube is filled with water. Now, the air column inside the tube is in unison with another fork of frequency f . Then
View SolutionA cylinderical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View SolutionThe end correction of a resonance colume is 1.0 cm.If the shortest length resonating with the tuning fork is `15.0` cm the next resonating length will be
View SolutionThe vibrating of four air columns are represented in the figure. The ratio of frequencies `n_(p): n_(q): n_(r) :" n_(s) ` is
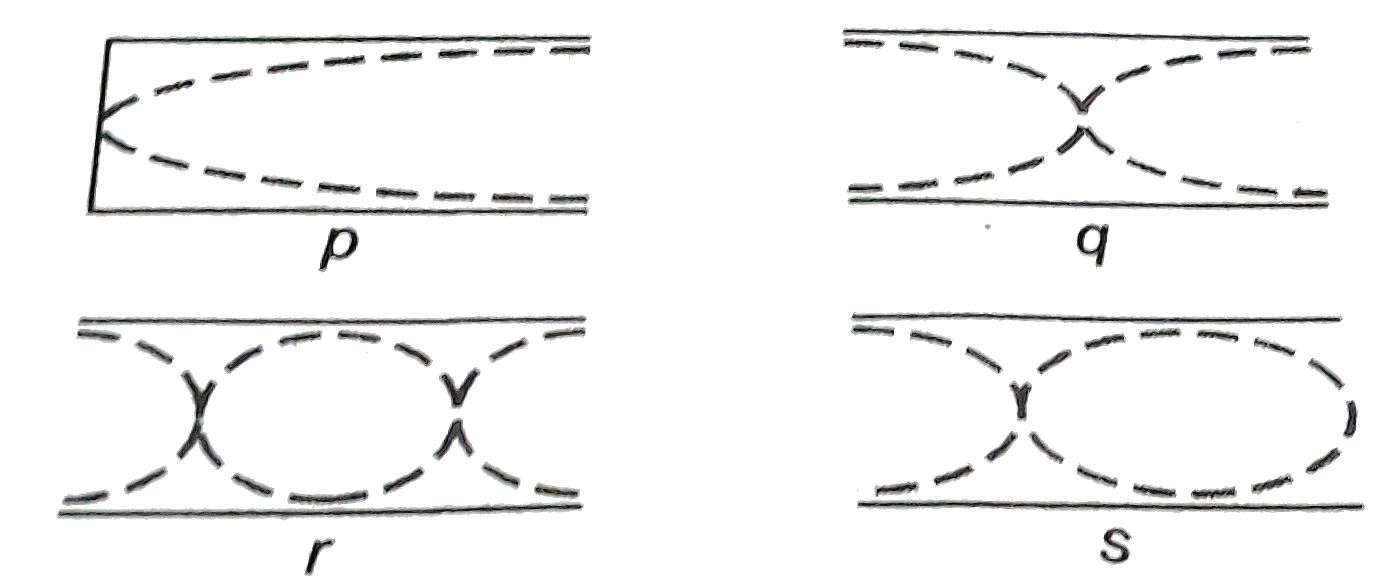
View SolutionAir is blown at the mouth of a tube of length 25 cm and diameter equal to 2 cm open at both ends. If velocity of sound in air is `330 ms^(-1)`, the sound emitted will have all the frequencies in the group
View SolutionA closed organ pipe of length 20 cm is sounded with tuning fork in resonance. What is the frequency of tuning fork? `(v = 332 ms^(-1))`
View SolutionAn orgen pipe open at one end is vibrating in first overtone and is in resonance with another pipe open at both ends and vibrating in third harmonic. The ratio of length of two pipes is
View SolutionIn a resonance column first and second resonance are obtained at depths `22.7` cm and `70.2` cm. The third resonance will be obtained at a depth of
View SolutionIn one metre long open pipe what is the harmonic of resonance obtained with a tuning fork of frequency 480 Hz
View SolutionA cylinderical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View Solution
EXERCISE 1 questions and complete solutions for chapter STATIONARY WAVES of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12