Complete Solutions to EXERCISE 12 C (Long Answer Type Questions ) of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| MODERN PUBLICATION | EXERCISE 12 C (Long Answer Type Questions ) |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
(i) One kind of cake requires 200 g of flour and 25 g of fat and another kind of cake requires 100 g of flour and 50 g of fat.Find the maximum number of cakes which can be made form 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.From a linear programming problem and solve it graphically.
(ii) One kind of cake requires 300 g of flour and 15 g of fat, another kind of cake requires 150 g of flour and 30 g of fat.Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 g of fat assuming that there is no shortage of the other ingredients used in making the cakes. Make it as an LPP and solve it graphically.
View SolutionReshma wishes to mix two types of food `P` and `Q` in such a way that the vitamin contents of the mixture contain at leat 8 units of vitamin A and 11 units of vitamin B. Food `P` cost Rs. 60/kg and Food `Q` costs Rs. 80/kg. Food `P` contains 3 units/kg of vitamin A and 5 units/kg of Vitamin B while food `Q` contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes `1. 5` hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
View SolutionIf a young man drives his car at 40 km per hour, he has to spend ₹ 5 per km on petrol, if he drives it at a slower speed of 25 km per hour, the petrol cost decreases to ₹ 2 per km. He has ₹ 100 to spend on petrol and wishes to find thhe maximum distance he can travel within one hour.Express this as a linear programming problem and then solve it.
View SolutionA dealer deals in two items A and B He has Rs. 15000 to invest and a space to store almost 80 pieces Item A costs him Rs 300 and item B costs him Rs. 150 He can sell items A and B at profits of Rs 40 and Rs 25 respectively Assuming that he can sell all that he buys formulate the above as a linear programming prioblem for maximum profit and solve it graphically
View SolutionA manufacture produceds two types of steel trunks. He has two machines, A and B. The second type required 3 hours on machine A and 2 hours n machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs.30 and Rs.25 per trunk of the first type and second type respectively. How many trunks of each type must he make each day to make the maximum profit?
View SolutionA factory manufatures two types pf screws A and B, Each type of screw requires the use of two machines, an automatic and a hand operated.It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B.Each machine is available for at the most 4 hours on any day.The manufacturer can sell a package of screws A at a profit of ₹ 7 and screws B at a profit of ₹ 10.Assuming that he can sell all the screws he amnufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit?Determine the maximum profit.
View SolutionA dealer wishes to purchase a number of fans and sewing machines. He has only Rs. 5,760 to invest and has a space for at most 20 items. A fan costs him Rs. 360 and a sewing machine Rs. 240. His expectation is that he can sell a fan at a profit of Rs. 22 and a sewing machine at a profit of Rs. 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize the profit? Formulate this as a linear programming problem and solve it graphically.
View Solution(i) A manufacturer produces nuts and bolts for industrial machinery.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit og ₹ 17.50 per package of nuts and ₹ 7.00 per package of bolts.How many packages of each should be produced each day so as to maiximise his profit, if he operate his machine for at the most 12 hous a day?Form an LPP for the problem and solve it graphically.
(ii) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on amchine A and 1 hour on machine B to produce a package of bolts.He earns a profit ₹35 per package of nuts and ₹14 per package of bolts.How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day? Convert it into an LPP and solve graphically.
View SolutionA shopkeeper manufactures gold rings and chains.The combined number of rings and chains manufactured per day is at most:(i) 16 (ii) 24 (iii)24
It takes (i) one hour (ii) half an hour (iii) one hour yo make a ring and (i) half an hour (ii) one hour (iii) half an hour for a chain.The maximum number of hours available is (i) 12(ii)16 (iii)16.
If the profit on a ring is :
(i)₹ 300 (ii) ₹ 100 (iii) ₹ 300
and on a chain is :
(i)₹ 200 (ii)₹ 300 (iii) ₹ 190.
How many of each should be manufactured daily, so as to maximize profti?Form an LPP and solve it graphically.
View SolutionA man has ₹1,500 for the purchase of Rice and Wheat.A bag of rice and a bag of wheat costs ₹ 180 and ₹ 120 respectively.He has storage capacity of 10 bags only.He earns a profit of ₹ 11 and ₹ 9 per bag of Rice and Wheat respectively.Formulate the problem as an LPP to find the number of bags of each type he should buy to maximize the profit and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assemb
View SolutionA merchant plans to sell two types of personal computers - a desktop model and a portable model that will cost Rs 25000 and Rs 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the nu
View Solution(Manufacturing problem) A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating a
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View SolutionTwo tailors A and B are paid ₹ 225 and ₹ 300 per day respectively.A can stitch 9 shirts and 6 pants while B can stitch 15 shirts and 6 pants per day.Form a linear programming problem to minimize the labour cost to produce at least 90 shirts and 48 pants.Solve the problem graphically.
View Solution(Allocation problem) A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profit from crops X and Y per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be
View SolutionA diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 units of calories. Two foods A and B are available at a cost of Rs. 5 and Rs. 4 per unit respectively. One unit of food A contains 200 units of vitamins, 1 unit of minerals and 40 units of calories whereas one unit of food B contains 100 units of vitamins, 2 units of minerals and 40 units of calories. Find what combination of the food A and B should be used to have least cost but it must satisfy the requirements of the sick person.
View SolutionFood X contains 6 units of vitamin A per gm and 7 units of vitamin B per gm and costs ₹ 2.00 per gm.Food Y contains 8 units of Vitamin A per gm and 12 units of vitamin B per gm and costs ₹ 2.50 per gm.The daily minimum requirement of vitamin A and vitamin V are 100 units and 120 units respectively.Formulate the above as a linear programming problem to minimize the cost.
View SolutionA diet is to contain at least 80 units of Vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs. 4 per unit and F2 costs Rs. 6 per unit. One unit of food F1 contains 3 units of Vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of Vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
View Solution(Diet problem): A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food "I" contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C.
View SolutionThere are two factories located one at place P and the other at place Q.From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirments of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
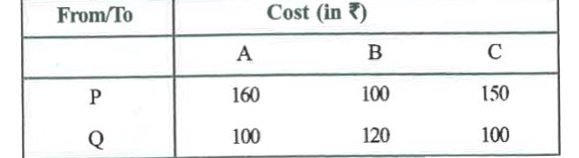
How many units should be transported from each factory to each depot in order that the transportable cost is minimum? When will be the minimum transportation cost?
View Solution
EXERCISE 12 C (Long Answer Type Questions ) questions and complete solutions for chapter LINEAR PROGRAMMING of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 MATHS LINEAR PROGRAMMING
- (FAQ)
- Chapter Test
- Check your understanding
- EXERCISE
- Exercise - 12.1
- EXERCISE 12 (C ) (B.Fill in the Blanks)
- EXERCISE 12 (C ) (True/False Questions)
- EXERCISE 12 (C ) (Very Short Answer Type Questions)
- EXERCISE 12 C (Long Answer Type Questions )
- EXERCISE 12 C (MULTIPLE CHOICE QUESTIONS)
- EXERCISE 12(a) (Short Answer Type Questions)
- EXERCISE 12(b) (Long Answer Tyoe Questions(I)) (LATQ)
- EXERCISE 12(b) (Short Answer Type Questions)
- Exercise 12.2
- FAQs
- ILLUSTRATIVE EXAMPLES
- Miscellaneous Exercise
- Revision Exercise