Complete Solutions to MCQ(Level-I) of chapter DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION |
| MODERN PUBLICATION | MCQ(Level-I) |
| Number Of Questions | 82 |
| Academic Year | 2023-24 |
Given `vec(A)=2 hat(i) - hat(j) + 2 hat(k)`. The unit vector of `vec(A) - vec(B)` is:
View SolutionA force of `(10 hat(i) - 3 hat(j) + 6hat(k))` newton acts on a body of mass 100 g and displaces it from `(6hat(i) + 5hat(j) - 3hat(k))` metre to `(10hat(i) - 2hat(j) + 7hat(k))`m. The work done is:
View SolutionA jeep is moving on a straight road due north with a uniform speed of 60 km `h^(-1)` . When it turns left through 90°. If the speed remains unchanged after turning, the change in the velocity of the jeep in the turning process is :
View SolutionThe magnitude of vectors `vec(A), vec(B)` and `vec(C)` are 12, 5 and 13 units and `vec(A) + vec(B) = vec(C)` . The angle between A and B is :
View Solution`vec(A)` and `vec(B)` are two vectors in a plane and `vec(C )` is a vector perpendicular to this plance their resultant is :
View SolutionIf `vec(A)=2 hat(i) + 3 hat(j) - hat(k)` and `vec(B)= 4 hat(i) + 6 hat(j) -2 hat(k)` the angle between `vec(A)` and `vec(B)`will be:
View SolutionIf `vec A =2 hat i+ 3 hat j+ 8 hat k` is perpendicular to `vec B= 4 hat j -4 hat i+ alpha hat k` , then the value of `alpha`
View SolutionWhat is the angle between x-axis and a force represented by `vec(F) = 2hat(i) + 3hat(j) + 4hat(k)` ?
View SolutionThe co-ordinates of moving particle at any time t are given by x = `at^(2)` and y = b`t^(2)`. The velocity magnitude of the particle :
View SolutionA body projected along an inclined plane of angle of inclination 300 stops after covering a distance `x_(1)`. The same body projected with the same speed stops after covering a distance `x_(2)` when the angle of inclination of the inclined plane is increased to `60^(@)` the ratio of `x_(1)//lx_(2)` is
View SolutionAfter time 't' the height ‘y ’ of projectile is y = 8t - 5`t^(2)` and horizontal distance x = 6t if g=10 m`s^(-2)1` , velocity of projectile at this instant is :
View SolutionA particle is projected with a velocity v so that its horizontal range twice the greatest height attained. The horizontal range is
View SolutionThree forces `(2 hat(i) - 3hat(j) + 4hat(k)),(8hat(i) - 7hat(j) + 6hat(k))` and `m(hat(i) - hat(j) + hat(k)` keep a body in equilibirium. The value of m is:
View SolutionTwo vectors of equal magnitude 'A' on addition give a resultant vector of magnitude 'A', then the magnitude of their difference vector is :
View SolutionA force vector applied on a mass is represented as `vec(F)=6 hat(i) - 8hat(j) + 10hat(k)` N and accelerates the mass at 5 `ms^(-2)` . The mass of the body is :
View SolutionRain is falling vertically downwards with a speed of 4 km `h^(-1)` . A girl moves on a straight road with a velocity of 3 km `h^(-1)` . The apparent velocity of rain with respect to the girl is :
View SolutionTwo forces each equal to `F/2`, act at right angles. Their effect may be neutralised by a third force acting along their bisector in the opposite direction with a magnitude of:
View SolutionGiven `vec(A) = 2hat(i) + 4hat(j) -6hat(k)`. When a vector `vec(B)` is added to `vec(A)` , we get a unit vector along x-axis. Then `vec(B)` is :
View SolutionA boat is sent across the river with a velocity of 8 km/h. in a direction perpendicular to flow of river. If resultant velocity of boat is 10 km/h, then velocity of river flow is :
View SolutionA projectile of mass m is fired with velocity v from a point P at `theta` = 45°. Neglecting air friction, the magnitude of change of momentum between the leaving pt. P and arriving pt. Q is :
View SolutionA gun fires two bullets at 60° and 30° with the horizontal the bullets strike at same horizontal distance. The maximum heights for the two bullets are in the ratio :
View SolutionAt what angle must the two forces (x + y) and (x - y) act so that the resultant may be `(x^(2) + y^(2))^(1//2)`:
View SolutionThree vectors `vec(A),vec(B)` and `vec(C)` satisfy the relation `vec(A).vec(B)=0` and `vec(A).vec(C )=0`. The vector `vec(A)` is parallel to:
View SolutionTwo balls are projected from the same point in directions inclined at 60° and 30° to the horizontal. If they attain the same maximum height, the ratio of their velocities of projection is :
View SolutionIf the angle between the vectors `vec(A)` and `vec(B)` is `theta`, the value of the product `(vec(B)xxvec(A)).vec(A)` is equal to:
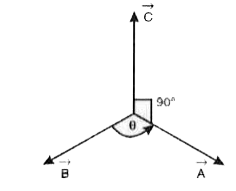
View SolutionThe greatest height to which a man can throw a stone is 100 m. The greatest distance to which he can throw it will be:
View SolutionA body is projected at an angle 30° with the horizontal with momentum p. At its highest point the magnitude of the momentum is :
View SolutionIf `vec(A).vec(B)=|vec(A)xxvec(B)|`, then the resultant of `vec(A)` and `vec(B)` is:
View SolutionIf R is the range and T is the time of flight of a projectile then the angle of projection is given by :
View SolutionA boat which has a speed 5 km/h in still water crosses a river 100 m along the shortest possible path in 1.5 min. The velocity of river water in km/h is :
View SolutionA persin moves 30 m north, then 20 m east and finally 30`sqrt(2)` m south-west. The displacement from the original position is :
View SolutionA projectile is projected with a kinetic energy K. Its range is R. It will have the minimum kinetic energy after covering the distance equal to :
View SolutionWhich of the following is the largest when the height attained by the projectile is the greatest:
View SolutionThe magnitude of the vector product of two vectors is `sqrt(3)` times their scalar product. The angle between the vectors is :
View SolutionIf a particle is at rest with three velocities of 14 units, 16 units and 26 units on it, then the angle between the directions of the two smaller velocities is :
View SolutionTwo projectiles, one fired from earth with 5 ms -1 and other fired from a planet with 3 ms -1 at the same angle trace identical trajectories. Neglecting friction, what is the acceleration due to gravity on planet ?
(g = 9.8 m`s^(-1)` ):
View SolutionThe height y and the distance x along the horizontal plane of a prohectile on a certain planet (with no surrounding atmosphere) are given by y=8t-`5t^(2)` meter and x=6t meter,where t is in seconds.The velocity with which the projectile is projected is
(Acceleration due to gravity =9.8 m `s^(-2)`)
View SolutionThe greatest height to which a man can throw a ball is ‘A’, the greatest distance to which he can throw it will be :
View SolutionA body is projected at an angle such that K.E. at the highest point is reduced to half the energy at point of projection. The angle of projection is :
View SolutionA large number of bullets are fired in all directions with same speed. What is the maximum area of their spread ?
View SolutionIn case of a projectile fired at an angle equally inclined to a horizontal and vertical with velocity v, the greatest height is given by :
View SolutionA body is projected at an angle of 45° with K.E. ‘E’. The K.E. at the highest point is :
View SolutionA ball whose kinetic energy is E is projected at an angle of `45^(@)` to the horizontal. The kinetic energy of the ball at the highest point of its flight willbe:
View SolutionA body is projected at an angle of 60° with the horizontal with momentum p. At its highest point the magnitude of the momentum is :
View SolutionFrom the top of a tower 40 m high a ball is projected upwards with a speed of 20 ms -1 at an angle 30° with the horizontal. The ratio of the total time of flight to hit the ground to the time taken by it to come back to the same initial elevation (g = 10 `ms^(-2)` ) is :
View SolutionThe ceiling of a hall is 25 m. What is the maximum distance at which a ball can be thrown inside the hall ?
View SolutionFigure shows the trajectory of a projectile fired at an angle `theta` with the horizontal. The elevation angle of the highest point as seen from the point of launching is `varphi`. The relation between `varphi` and `theta` is :

View SolutionA ball is projected upwards from the top of a tower with velocity 50 m`s^(-1)` making an angle of 30° with the horizontal. If the height of the tower is 70 m, after what time from the instant of throwing, will the ball reach the ground (g = 10 `ms^(-2)` ):
View SolutionA fighter plane flying horizontally passes over an antiaircraft gun with a uniform velocity 200 m`s^(-1)` . The gun can fire the shell with a velocity 200`sqrt(2)ms^(-1)` . At what angle should the gun fire the shell so as to hit the plane ?
View SolutionIn the above question what should be the minimum height of plane so that it may not be hit by the shell ? (g = 10 `ms^(-2)` ):
View SolutionConsider `vec(F)=4hat(i) - 3hat(j)`. A vector perpendicular to `vec(F)` is :
View SolutionThe angle between the vectors `vec(A)` and `vec(B)` is `theta`. The value of triple Product `vec(A).vec(B)xxvec(A)` is :
View SolutionWith respect to a rectangular cartesian co-ordinate system three vectors are expressed as : `vec(a)=4hat(i) - hat(j),vec(b)=-3 hat(i) + 2hat(j):vec( c)=-hat(k)` . The unit vector `hat(r)`, along the direction of the sum of these vectors is :
View SolutionA particle of mass m is projected with velocity v making an angle of 45 with horizontal. Magnitude of angular momentum of particle about the point of projection when the particle is at its maximum height is
View SolutionIn the arrangement shown in the fig. the ends P and Q
color
of a string are being moved downwards with a speed of v each. The pulleys are fixed. The mass M moves upwards with a speed of :
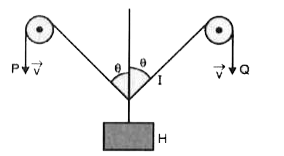
View SolutionFind the torque due to force `vec(F)=2g=hat(i) -3hat(j)+4hat(k)` newton acting a point with position vector `vec(r )=3hat(i) + 2hat(j) + 3hat(k)` metre about the origin :
View SolutionThe equation of projectile is `y=sqrt(3)-g/2x^(2)` , the angle of its projection is :
View SolutionA projectile has same range R for the two angles of projection. If `T_(1)` and `T_(2)` are the times of flight in two cases, then:
View SolutionA projectile is thrown at an angle `theta` with the horizontal and its range is `R_(1)` It is then thrown at an angle 0 with vertical and the range is `R_(2)` then :
View SolutionTwo projectiles A and B are thrown from the same point with velocities v and `v/2` respectively. If B is thrown at an angle 45° with horizontal, what is the inclination of A when their ranges are the same ?
View SolutionAn object of mass 3 kg is at rest. A force `vec(F)=6hat(i)t^(2) + 4hat(j)t` is applied, then velocity of the object at t = 3 second is :
View SolutionA particle moves with velocity `(6hat(i)-4hat(j) + 3hat(k))ms^(-1)` under the influence of a constant force F = `20 hat(i) + 15hat(j) -5 hat(k)` N. The instantaneous power applied to the particle is:
View SolutionTwo boys are standing at the ends A and B of a ground where AB = 'a'. The boy at B starts running in a direction perpendicular to AB with a velocity The boy at A also starts running simultaneously with velocity v in straight line and catches the B in time then t is :
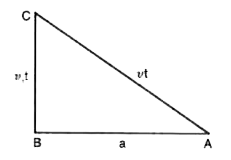
View SolutionA projectile is projected with initial velocity (`6hat(i) + 8hat(j)`) m`s^(-1)` if g = 10 `ms^(-2)` , then horizontal range is :
View SolutionA projectile is projected in vacuum at an angle 0, then square of the time it takes to reach the highest point shall be :
View SolutionIf the vectors `vec(P)=ahat(i) + ahat(j) + 3hat(k)` and `vec(Q)=ahat(i) -2hat(j) - hat(k)` are perpendicular to each other, then positive value of a is :
View SolutionMaximum height of a bullet when fired at 30° with the horizontal is 11m. Then height when it is fired with the horizontal at 60° is :
View SolutionThe resultant of two forces is 20 N when one of force is 20`sqrt(3)` N and angle between two forces is 30° then what is value of second force ?
View SolutionA body projected at an angle 45° with horizontal has range 16 m. It explodes into two parts of equal masses at the highest point. One of parts falls downwards at the point of explosion. At what distance from the point of throw, the other will fall ?
View SolutionA particle moves in X-Y plane under the action of forces F such that the values of linear momentum 'p' at any times is `p_(x) = 2 cos t` and `p_(y) = 2 sin t` . The angle between `vec(F)` and at the time t will be:
View SolutionAn object is projected with velocity 20 `ms^(-1)` making an angle of 45° with horizontal. The equation for its trajectory is `h = Ax - Bx^(2)` where h is the height and x the horizontal distance at any instant. The ratio of constant A:B is:
View SolutionA projectile is projected with a speed K Ve where Ve is escape velocity and K is a constant less than one. The maximum height reached by it from the centre of earth will be :
View SolutionIf the relation between range R and time of flight T is given by R = 5 T2 , the angle of throw of the projectile is :
View SolutionA projectile of mass m is thrown with a velocity v making an angle 60° with the horizontal. Neglecting air resistance, the change in momentum from the departure A to its arrival at B, along the vertical directions :

View SolutionA projectile is thrown with initial velocity `ahat(i) + bhat(j)` m/s. If range of projection is twice the maximum height reached by it then :
View SolutionIf `vec(A)=3hat(i) + 4hat(j)` and `vec(B)=7hat(i) + 24hat(j)`. Find the vector having the same magnitude as `vec(B)` and is parallel to `vec(A)`:
View SolutionThe co-ordinates of a moving particle at any time 't' are given by `x = alphat^(3)` and `y = betat^(3)`. The speed of the particle at time Y is given by :
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle of 30° with the horizontal. How far from the throwing point will be ball be at the height of 10 m from the ground ?
`[g=10ms^(-2),sin30^@=1/2,cos30^@=sqrt(3)/2]`
View SolutionThree forces start acting simultaneously on a particle , moving with velocity, `vec(v)` . These forces are represented in magnitude and direction by the three sides of a triangle ABC (as shown). The particle will now move with velocity
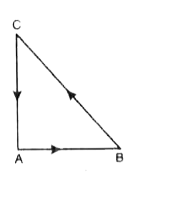
View SolutionIf `vec(A)xxvec(B)=vec(B)xxvec(A)`, then the angle between A and B is:
View SolutionA particle is projected at 60° to the horizontal with a kinetic energy K. The kinetic energy at the highest point is:
View SolutionA particle has an initial velocity of `3hat(i) + 4hat(j)` and an A A acceleration of `0.4 hat(i) + 0.3 hat(j)` . Its speed after 10 s is :
View Solution
MCQ(Level-I) questions and complete solutions for chapter DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12