Complete Solutions to MCQ(LEVEL-II) of chapter DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION |
| MODERN PUBLICATION | MCQ(LEVEL-II) |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
The vector sum of two forces is perpendicular to their vector differences. In that case, the forces :
View SolutionThe equations of motion of a projectile are given by x = 36t metre and `2y = 96t - 9.8r^(2)` metre. The angle of projection is :
View SolutionTwo particles having position `vec(r_(1))=(3hat(i) + 5hat(j))` meter and `vec(r_(2))=(-5hat(i)-3hat(j))` metre are moving with velocities `vec(V_(1))=(4hat(i)+hat(j))`m/s and `vec(V_(2))=(ahat(i) + 7hat(j))` m/s. If they collide after 2 seconds, the value of `a` is :
View SolutionThe sum of the magnitude of two vectors is 18. The magnitude of their resultant is 12. If the resultant is perpendicular to one of the vectors, then the magnitudes of the two vectors are :
View SolutionWhen `vec(A).vec(B)=-|A|.|B|` then :
View SolutionIf retardation produced by air resistance of projectile is one-tenth of acceleration due to gravity, the time to reach maximum height:
View SolutionFor a given angle of projection, if the time of flight of a projectile is doubled, the horizontal range will increase to :
View SolutionIf `|vec(A)xxvec(B)|=sqrt(3)vec(A).vec(B)` then the value of `|vec(A) + vec(B)|`is :
View SolutionFor angles of projection of projectiles at (`45° -theta`) and (`45° + theta`) the horizontal ranges described by the projectile are in the ratio
View SolutionWhich of the following statement is correct about the scalar quantity ?
View SolutionTwo vectors `vec(u)` and `vec(v)` given by `vec(u) = ahat(i)+bhat(j)` and `vec(v)=phat(i) + qhat(j)` have their orientation in the plane XY as shown in the fig. Which of the statements will apply correctly to them.
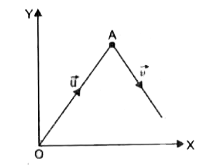
View SolutionThe two vectors are `vec(A) = hat(i) + hat(j)` and `vec(B) = hat(i) - hat(j)` . What is the angle between them ?
View SolutionThe component of a vector `vec(r)` along x- axis will have a maximum value if
View SolutionThe horizontal range of a projectile projected with a velocity V at angle 15° with the horizontal is 50 m. What will be its horizontal range if its angle of throw is increased by 30° keeping the velocity of throw to be the same ?
View SolutionIf the vectors `vec(a)` and `vec(b)` are such that `|vec(a) + vec(b)|=|vec(a)|` then does it imply that:
View SolutionIf `|vec(a) + vec(b)| = |vec(a) - vec(b)|` then
View SolutionAn aeroplane is flying at a height of 2000 m above the ground horizontally with a uniform speed of 720 km/h. At what angle of sight (w.r. to the horizontal) should the pilot drop a bomb so as to hit target on the ground ?
View SolutionThe torque of a force `vecF=-3hati+hatj+5hatk` acting at a point is `vectau`. If the position vector of the point vector of the point is `7hati+3hatj+hatk`, then `vectau` is :
View SolutionThe position vectors of radius are `vec(r_(1))=2hati+hatj + hatk` , `vec(r_(2))=2hati - 3hatj + hatk` while those of linear momentum are `2hati + 3hatj - hatk`. The angular momentum is :
View SolutionA force vector applied on a mass is represented by `vec(F)=6hati + 8hatj+10hatk` and it accelerates it with 1 m`s^(-1)` . What will be the mass of the body ?
View SolutionWhich vector should be added to `2hati + 4hatj -3hatk` and `3hati-5hatj+7hatk` to get a unit vector along y-axis ?
View SolutionThe sum of the magnitude of two vectors is 18. The magnitude of their resultant is 12. If the resultant is perpendicular to one of the vectors, then the magnitudes of the two vectors are :
View SolutionIf unit vectors `vec(A)` and `vec(B)` are inclined at an angle `theta` then `|vec(A)-vec(B)|` is:
View SolutionAngle which the vector `vec(A)=2hati + 3hatj` makes with the y-axis is given by :
View SolutionIf the magnitude of the vector product is `sqrt(3)` times the magnitude of the scalar product, the angle between the two vectors is :
View SolutionA particle of mass m = 5 is moving with uniform speed v = `3sqrt(2)` in the XOY plane along the line Y = X + 4. The magnitude of angular momentum of the particle about the origin is :
View SolutionThe velocity of projection of an oblique projectile is `(6hati + 8hatj)ms^(-1)` horizontal range of the projectile is:
View SolutionA projectile is thrown at angel with vertical. It reaches a maximum height H. The time taken to reach the highest point of its path is :
View SolutionA ball is projected from a certain point on the surface of a planet at a certain angle with the horizontal surface. The horizontal and vertical displacements x and y vary with time t in second as `x=10sqrt(3)t` and `y=10t-t^(2)`
The maximum height attained by the ball is:
View SolutionIf the air resistance causes a vertical retardation of 10% of value of acceleration due to gravity, then the time of flight of an oblique projectile will be decreased by nearly:
View SolutionA body is thrown horizontally with a velocity `sqrt(2gh)` from the top of a tower of height h. It strikes the level ground through the foot of the tower at a distance x from the tower. The value of x is :
View SolutionThe range of the projectile for a given initial velocity of projection is minimum, if the angle of projection is :
View SolutionA ball is projected at an angle 30° with the horizontal. What is the component of acceleration along the velcoity of projection ?
View SolutionA particle is projected at an angle of 45° from the foot of a wall, just touches the top of the wall and falls on the ground on the opposite sides at a distance 4 m from it. The height of wall is :
View SolutionThe equation of projectile is `y=sqrt(3)-g/2x^(2)` , the angle of its projection is :
View SolutionA projectile is thrown from a point in a horizontal plane such that its horizontal and verticaly velocity components are 9.8 and 19.6 m `s^(-1)` respectively. It strikes the ground after covering a horizontal distance of :
View SolutionA projectile is fired at 45° with a speed of 200 m`s^(-1)` . Its maximum height will be the same as that for a projectile fired vertically upwards with a speed of:
View SolutionThe initial velcoity of particle `vec(u)=4 hati + 3hatj`. It is moving with uniform acceleration `vec(a) = 0.4 hati+0.3 hatj` . Its velocity after 10 seconds is :
View SolutionA rod of length 'l' rests at a point A against a smooth vertical wall while end B is on the floor as shown in the fig. If the end A moves uniformly downwards, what will be the velocity of the end B if x is the distance of point B from wall.
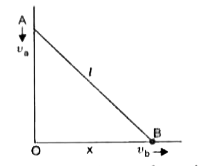
View SolutionTwo projectiles are thrown from the same point simultaneously with same velocity 10 m`s^(-1)` . One goes straight vertically while other at 60° with the vertical. What will be the distance of separation between the two after 1 second of their throw ?
View SolutionIf `vec(A)=2hati + 3hatj` and `vec(B)=hati + hatj`, then the vector component of `vec(A)` in the direction of `vec(B)` is :
View SolutionAn object is projected with velocity 20 `ms^(-1)` making an angle of 45° with horizontal. The equation for its trajectory is `h = Ax - Bx^(2)` where h is the height and x the horizontal distance at any instant. The ratio of constant A:B is:
View SolutionA stone is thrown with a velocity v at an angle 0 with the horizontal. Its speed when it makes an angle /3 with the horizontal is :
View SolutionShow that a projectile fired at an angle 0 with the horizontal crosses a certain height at two timings `t_(1)` and `t_(2)` and the sum of these two is equal to :
View SolutionIf `vec(A)=3hat(i) + 4hat(j)` and `vec(B)=7hat(i) + 24hat(j)`. Find the vector having the same magnitude as `vec(B)` and is parallel to `vec(A)`:
View SolutionA particle moves in X-Y plane under the action of forces F such that the values of linear momentum 'p' at any times is `p_(x) = 2 cos t` and `p_(y) = 2 sin t` . The angle between `vec(F)` and at the time t will be:
View SolutionIf the relation between range R and time of flight T is given by R = 5 T2 , the angle of throw of the projectile is :
View SolutionGiven : `vec(a) + vec(b) + vec(c) = 0` . Out of the three vectors `vec(a), vec(b)` and `vec(c)` , two are equal in magnitude. The magnitude of the third vector is `sqrt(2)` times that of either of the two having equal magnitude. The angles between the vectors are :
View SolutionThe resultant of three vectors 1, 2 and 3 units whose directions are those of the sides of an equilateral triangle is :
View SolutionWhen a projectile is moving at 60 m `s^(-1)` at the highest point of its trajectory, it explodes into two equal parts. One part moves vertically up with a velocity of 50 `ms^(-1)` . The magnitude of velocity of other part is:
View SolutionA projectile can have the same range 'R' for two angles of projection. If `t_(1)` and `t_(2)` be the times of flight in the two cases, then product of the two times of flights is proportional to :
View SolutionA body is at rest at x = 0. At t = 0, it starts moving in the positive x-direction with a constant acceleration. At the same instant another body passes through x = 0 moving in the positive x-direction with a constant speed. The position of the first body is given by `X_(1)` (r) after time t and that of the second body by `x_(2)` (r) after the same time interval. Which of the following graphs correctly describes (`x_(1) - x_(2)` ) as a function of time t?
View SolutionConsider a rubber ball freely falling from a height h = 4.9 m on to a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic.
Then the velocity as a function of time and the height as a function of time will be :
View SolutionA particle is moving with velocity `vec(v)=K(yhati + xhatj)`, where K is a constant. The general equation for its path is:
View Solution
MCQ(LEVEL-II) questions and complete solutions for chapter DESCRIPTION OF MOTION IN TWO AND THREE DIMENSION of MODERN PUBLICATION PHYSICS (KANNADA ENGLISH) of Class 12