Complete Solutions to EXERCISE -4 of chapter ATOMS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMS |
| NARAYANA | EXERCISE -4 |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
Magnetic moment due to the motion of the electron in `n^(th)` energy state of hydrogen atom is proportional to :
View SolutionThe ratio between total acceleration of the electron in singly ionized helium atom and hydrogen atom (both in ground state) is
View SolutionThe shortest wavelength of the Brackett series of a hydrogen-like atom (atomic number of `Z` ) is the same as the shortest wavelength of the Balmer series of hydrogen atom. The value of `z` is
View SolutionAccording to Bohr's theory of hydrogen atom , the product of the binding energy of the electron in the nth orbit and its radius in the nth orbit
View SolutionIf an electron drops from 4th orbit to 2nd orbit in an H-atom, then
View SolutionThe enrgy of an atom (or ion) in the ground state is `- 54.4 eV ` .If may be
View SolutionAn atom absorb `2eV`energy and is excited to next energy state . The wavelength of light absorbed will be
View SolutionWhen an electron in the hydrogen atom in ground state absorb a photon of energy `12.1eV`, its angular momentum
View SolutionMagnetic field at the center (at nucleus) of the hydrogen like atom `("atomic number" = z)` due to the motion of electron in nth orbit is proporional to
View SolutionA neutron moving with a speed `v` makes a head-on collision with a hydrogen in ground state kept at rest which inelastic collision will be take place is (assume that mass of photon is nearly equal to the mass of neutron)
View SolutionA charge particle is moving in a uniform magnetic field ib a circular path. The energy of the particle is doubled . If the initial radius of he circular path was `R`, the radius of the new circular path after the energy is doubled will be
View SolutionAn electron in hydrogen atom after absorbing an energy photon jumps from energy state `n_(1)` to `n_(2)`. Then it returns to ground state after emitting six different wavelength in emission spectrum. The energy of emitted photons is either equal to, less than or greater than the absorbed photons. then `n_(1)` and `n_(2)` are
View SolutionThe photon radiated from hydrogen corresponding to `2^(nd)` of Lyman series is abosorbed by a hydrogen like atom `'X'` in `2^(nd)` excited state. As a result the hydrogen like atom `'X'` makes a transition to `n^(th)` orbit. Then :
View SolutionIn a hypothetical system , a partical of mass `m` and charge `-3 q` is moving around a very heavy partical chaRGE `q`. Assume that Bohr's model is applicable to this system , then velocuity of mass `m` in the first orbit is
View SolutionConsider a hydrogen-like atom whose energy in nth excited state is given by
`E_(n) = (13.6 Z^(2))/(n^(2))`
When this excited makes a transition from excited state to ground state , most energetic photons have energy
`E_(max) = 52.224 eV`. and least energetic photons have energy
`E_(max) = 1.224 eV`
Find the atomic number of atom and the intial state or excitation.
View Solution29 electrons are removed from Zn-atom (Z=30)by certain means. The minimum energy needed to remove the 30th electron, will be
View SolutionThe ionisation energy of `Li^(2+)` atom in ground state is,
View SolutionA photon of energy `15eV` collides with `H-`atom. Due to this collision, `H-`atom gets ionized. The maximum kinetic energy of emitted elecrtron is:
View SolutionMonochromatic radiation of wavelength `lambda` is incident on a hydrogen sample in ground state. Hydrogen atoms absorb a fraction of light and subsequently emit radiations of six different wavelength . Find the wavelength `lambda`.
View SolutionThe follwing diagram indicates the energy levels of a certain atom when the system moves from `2E` level to `E`, a photon of wavelength `lambda` is emitted. The wavelength of photon produced during its transition from `(4E)/(3)` level to `E` is

View SolutionWhen the electron in a hydrogen atom jumps from the second orbit to the first orbit , the wavelength of the radiation emitted is `lamda` . When the electron jumps from the third orbit to the first orbit , of the same atom , the wavelength of the emitted radiation would be
View SolutionThe ratio of the largest to shortest wavelength in Balmer series of hydrogen spectra is,
View SolutionThe electron in hydrogen atom makes a transition `n_(1)ton_(2)` where `n_1` and `n_2` are the principal quantum number of two states. Assuming the Bohr model to be valid, the time period of the electron in the initial state is eight times that in the final state. The possible value of `n_1` and `n_2` are:
View SolutionAny radiation in the ultraviolet region of hydrogen spectrum is able to eject photoelectrons from a metal. What should be the maximum value of threshold frequency for the metal?
View SolutionA hydrogen atom emits a photon corresponding to an electron transition from `n = 5` to `n = 1`. The recoil speed of hydrogen atom is almost (mass of proton `~~1.6 xx 10^(-27) kg)`.
View SolutionThe wave number of energy emitted when electron jumps from fourth orbit to second orbit in hydrogen in `20,497cm^(-1)`. The wave number of energy for the same trasition in `He^(+)` is
View SolutionIn a Bohr atom the electron is replaced by a particle of mass `150` times the mass of the electron and the same charge. If `a_(0)` is the radius of the first Bohr's orbit of the orbital atom, then that of the new will be .
View SolutionIf the wavelength of the first member of Balmer series of hydrogen spectrum is `6564A^(@)` , the wavelength of second member of Balmer series will be:
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited state of quantum number 'n' this excited atom can make a transition to the first excited state by emitting a photon of first `27.2eV`. Alternatively the atom from the same excited state can make a transition to the 2nd excited state by emitting photon of energy `10.20eV` the value of `n` and `z` are given (ionization energy of hydrogen atom is 13.6eV)
View SolutionPhoton from `n=2` to `n=1` in hydrogen atom is made to fall on a metal surface with work function `1.2eV.` The maximum velocity of photo electron emitted is nearly equal to
View SolutionLet `nu_(1)` be the frequency of the series limit of the lyman series `nu_(2)` be the frequency of the first line of th lyman series and `nu_(3)` be the frequency of the series limit of the Balmer series. Then
View Solution(a) (i) Find the wavelength of the radiation required to excite thye elctron in `Li(++)` from the first to the third Bohr orbit.
(ii) How many spectal lines are observed in the emission spectrum of the above excited system ?
(b) The energy needed to detach the electron of a hydrogen-like ion in ground state in 4 rydberg.
(i) What is the wavelength of the radiation emitted when the electron jumps from the first excited state ot the ground state ?
(ii) What is the radius of first orbit ?
(c ) A hydrogen sample is prepared in a particular excited state A. Photons of energy 2.55 eV get absorbed into the sample to take some electrons to a further excited state B. Find the quantum number of the A and B.
(d) A hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with excitation energy 10.2 eV. (i) Identify the quantum number n of the upper and the lower energy states.
Find `lambda`.
View SolutionFind the wavelength in a hydrogen spectrum between the range `500nm to 700nm`
View SolutionThe largest wavelength in the ultraviolet region of the hydrogen spectrum is 122 nm. The smallest wavelength in the infrared region of the hydrogen spectrum (to the nearest integer) is
View SolutionThe electric potential between a proton and as electron is given by `V= V_(0) ln (r )/(r_(0))` , where`r_(0)` is a constant . Assuming Bohr's model to be applicable , write variation of `r_(n)` with `n,n` being the principal quantum number ?
View SolutionIf elements of quantum number greater than `n` were not allowed , the number of possible electrons in nature would be ?
View SolutionMagnetic field at the center (at nucleus) of the hydrogen like atom `("atomic number" = z)` due to the motion of electron in nth orbit is proporional to
View SolutionThe recoil speed of a hydrogen atom after it emits a photon in going from `n=5`, state to `n=1` state is (in `ms^(-1)`)
View SolutionThe binding energy of an electron in the ground state of He atom is `E_(0)=24.7eV`. The energy required to remove both the elements from the atom is
View SolutionIn hydrogen atom, the radius of `n^(th)` Bohr orbit is `r_(n)`. The graph Beetwee n `log .(r_(n)/r_(1))` will be
View SolutionIn hydrogen atom, the area enclosed by `n^(th)` orbit is `A_(n)`. The graph between log `(A_(n)/A_(1))` log will be
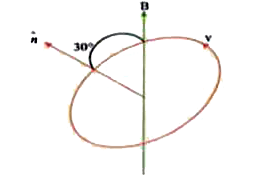
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in the circular orbit of radius R. The atom is placed in a uniform magnetic induction B such that the plane normal of electron orbit makes an angle `30^@` with B, as shown in figure. The torque experienced by electron will be
 .
.
View Solutionif we assume only gravitational attraction between proton and electron in hydrogen atom and the Bohr quantizaton rule to be followed, then the expression for the ground state energy of the atom will be (the mass of proton is M and that of electron is m.)
View SolutionTaking the Bohr radius `a_(0) = 53` pm, the radius of `Li^(++)` ion in its gnround state, on the basis of Bohr's model, will be about.
View SolutionThe simple Bohr model cannot be directly ap-plied to calculate the energy level of an atom with many electrons . This is because.
View SolutionTwo H atoms in the ground state collide in elastically. The maximum amount by which their combined kinetic energy is reduced is
View SolutionA set of atom in an excited state decays
View Solution
EXERCISE -4 questions and complete solutions for chapter ATOMS of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS ATOMS
- C.U.Q
- C.U.Q (INTRODUCTION)
- C.U.Q ALPHARAY SCATTERING
- C.U.Q BOHR.S THEORY
- EVALUATE YOURSELF -1
- EVALUATE YOURSELF -2
- EVALUATE YOURSELF -3
- EXERCISE -1 (C.W) ALPHARAY SCATTERING
- EXERCISE -1 (C.W) ATOMIC SPECTRA
- EXERCISE -1 (C.W) BOHR.S MODEL OF ATOM
- EXERCISE -1 (C.W) INTRODUCTION
- EXERCISE -1 (H.W) ALPHA RAY SCATTERING
- EXERCISE -1 (H.W) ATOMIC SPECTRA
- EXERCISE -1 (H.W) BOHR.S MODEL OF ATOM
- EXERCISE -1 (H.W) INTRODUCTION
- EXERCISE -2 (C.W) ALPHARAY SCATTERING
- EXERCISE -2 (C.W) ATOMIC SPECTRA
- EXERCISE -2 (C.W) BOHR.R THEORY
- EXERCISE -2 (C.W) INTRODUCTION
- EXERCISE -2 (H.W) ALPHARAY SCATTERING
- EXERCISE -2 (H.W) ATOMIC SPECTRA
- EXERCISE -2 (H.W) BOHR.S THEORY
- EXERCISE -2 (H.W) INTRODUCTION
- EXERCISE -3
- EXERCISE -4
- illustrstion