Complete Solutions to आंकिक उदाहरण of chapter वैधुत आवेश और क्षेत्र of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | वैधुत आवेश और क्षेत्र |
| NAVBODH PARIKSHA SAAR | आंकिक उदाहरण |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
एक चालक पर `14 *4 xx 10 ^(-19 )` कूलॉम धनावेश है । इस चालाक पर कितने इलेक्ट्रॉनों की अधिकता या कमी है ?
02:27View Solutionएक पॉलीथिन के टुकटे को उन से रगड़ने पर उसमे `4*8xx10^(-7)` कूलॉम का तरणवेश उत्पन्न हो जाता है । उन पॉलीथिन में स्थानांतरित होने वाले इलेक्ट्रॉनों की संख्या क्या होगी ? पॉलीथिन के द्रव्यमान में वृद्धि की गणना कीजिए ।
04:04View Solutionनाभिक `""_(7 ) N ^(14 )` पर कूलॉम में आवेश की गणना कीजिए ।
01:40View Solutionएक कप जल में कितने धनावेश तथा तरणवेश होते है यदि एक कप जल का द्रव्यमान 250 g है ?
07:03View Solutionयदि किसी पिंड से एक सेकंड में `10 ^(9 )` इलेक्ट्रॉन किसी अन्य पिंड से स्थानांतरित होते है तो 1C आवेश के स्थानांतरण में कितना समय लगेगा ?
04:38View Solutionदो प्रोटॉनों के बीच लगने वाले बल की गणना कीजिए यदि इनके बीच की दुरी `4*0xx10^(-15)` मीटर है ।
01:55View Solutionधनावेश से आवेशित दो आयन एक-दूसरे को `3*7 xx10^(-9)` न्यूटन के बल से प्रतिकर्षण करते है । यदि उनके बीच की दुरी `5Å`हो, तो बताइये प्रत्येक आयन में कितने इलेक्ट्रॉनों की कमी होगी ?
04:09View Solutionदो प्रोटॉनों के बीच लगने वाला बल उनमे से किसी एक के भार के बराबर है । उनके बीच की दुरी ज्ञात कीजिए ।
02:22View Solutionएक स्वतंत्र मज्जा गुटिका A पर , जिसका द्रव्यमान 8 ग्राम है, `5xx10^(-8)` कूलॉम धन आवेश है । इस गुटिक के निचे 5 सेमी निचे एक दूसरी मज्जा गुटिका B स्थिर राखी है । इस मज्जा गुटिका को किस प्रकृति का कितना आवेश दिया जाये जिससे की मज्जा गुटिका A स्थिर रह सके ?
04:41View Solutionदो बिंदु आवेशों का योग `7muC ` है । जब वे मुक्त आकाश में 30 सेमि की दुरी पर होते है तो एक-दूसरे के 1 न्यूटन के बल से प्रतिकार४षित करते है । प्रत्येक आवेश का मान ज्ञात कीजिए ।
04:28View Solutionदो बिंदु आवेश, जिनमे से प्रत्येक पर आवेश की मात्रा समान है, एक-दूसरे से 1 मीटर की दुरी पर रखने पर 8 न्यूटन के बल से प्रतिकर्षित करते है । अब यदि उन्हें जल के अंदर उतनी ही दुरी पर रखा जाए तो बे कितने बल का अनुभव करेंगे ?
(दिया है- -`K _( जल)=80 )`03:27View Solutionकिसी आवेश q को भागो `q _(1 )` और `q _(2 )` में विभाजित कर किसी दुरी पर रखा जाता है । `q _(1 )` और `q _(2 )`में सम्बन्ध स्थापित कीजिए ताकि उनके मध्य लगने वाला प्रतिकर्षण बल अधिकतम हो ।
05:50View Solution`5muC` , `10muC ` और `-10muC ` के तीन आवेश 5 सेमी भुजा के समबाहु त्रिभुज के सिरे A ,B और C पर रखे गए है । सिरे A पर स्थित परिणामी बल एव दिशा की गणना कीजिए ।
06:00View Solutionइलेक्ट्रॉन और प्रोटोन के पारस्परिक आकर्षण के वैधुत बल के कारन इलेक्ट्रॉन तथा प्रोटॉन के त्वरण का आकलन कीजिए जबकि इनके बीच की दुरी `1Å(=10 ^(-10)m )` है । ` (m _(1p) =1*67 xx10^(-27)kg ` तथा `m _(e) =9*11 xx10^(-31) kg )`
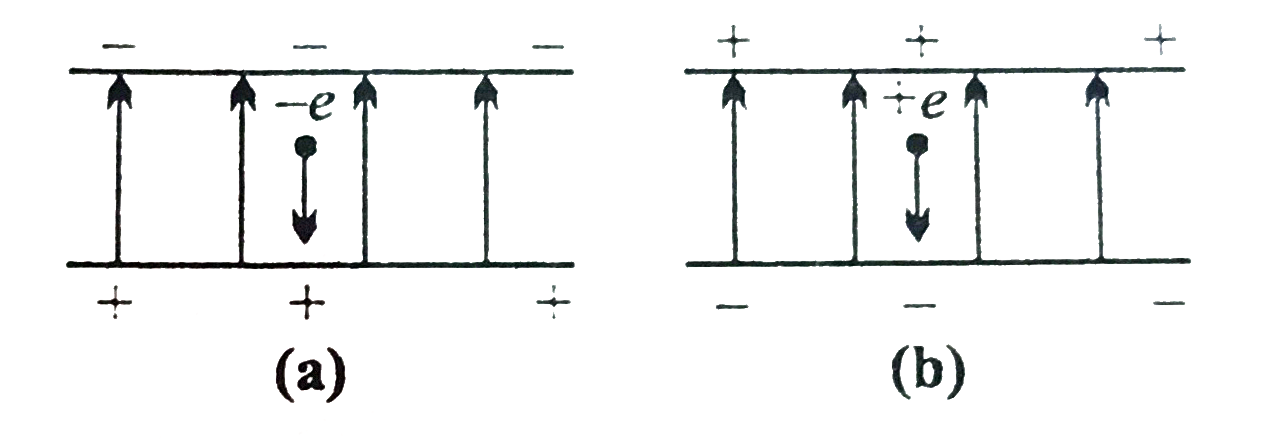
05:25View Solutionधातु का आवेशित गोला A नाइलोन के घागे से निलंबित है । विधूतरोधी हत्थि द्वारा किसी अन्य धातु के आवेशित गोले B को A के इतने निकट लाया जाता है चित्र (a ) में दर्शाए अनुसार इनके केन्द्रो के बीच की दुरी 10cm है । गोले A के परिणामी प्रतिकर्षण को नॉट किया जाता है। (उधारणार्थ-गोले पर चमकीला प्रकाश पुंज डालकर तथा अंशाकित परदे पर बानी चाय का विक्षेपण मापक) । A तथा B गोलों को चित्र (b ) में दर्शाए अनुसार क्रमशः अनावेशित गोले C तथा D से स्पर्श कराया जाता है । तत्पश्चात चित्र (c ) में दर्शाए अनुसार C तथा D को हटाकर B को A के निकट लाया जाता है कि इनके केन्द्रो के बीच कि दुरी `5 *0 कम ` हो जाती है । कूलॉम नियम के अनुसार A का कितना अपेक्षित प्रतिकर्षण है । गोले A तथा C एव गोले B तथा D के आकार सर्वसम है । A तथा B के केन्द्रो के पृथकन कि तुलना में इनके ाकारो कि उपेक्षा कीजिए ।
 View Solution
View Solutionचित्र में दर्शाए अनुसार किसी समबाहु त्रिभुज के शीर्षो पर स्थित आवेशों q ,q तथा -q पर विचार कीजिए । प्रत्येक आवेश पर कितना बल लग रहा है ? त्रिभुज की प्र्तेक आवेश पर कितना बल लग रहा है ? त्रिभुज की प्रत्येक भुजा की लम्बाई l है ।
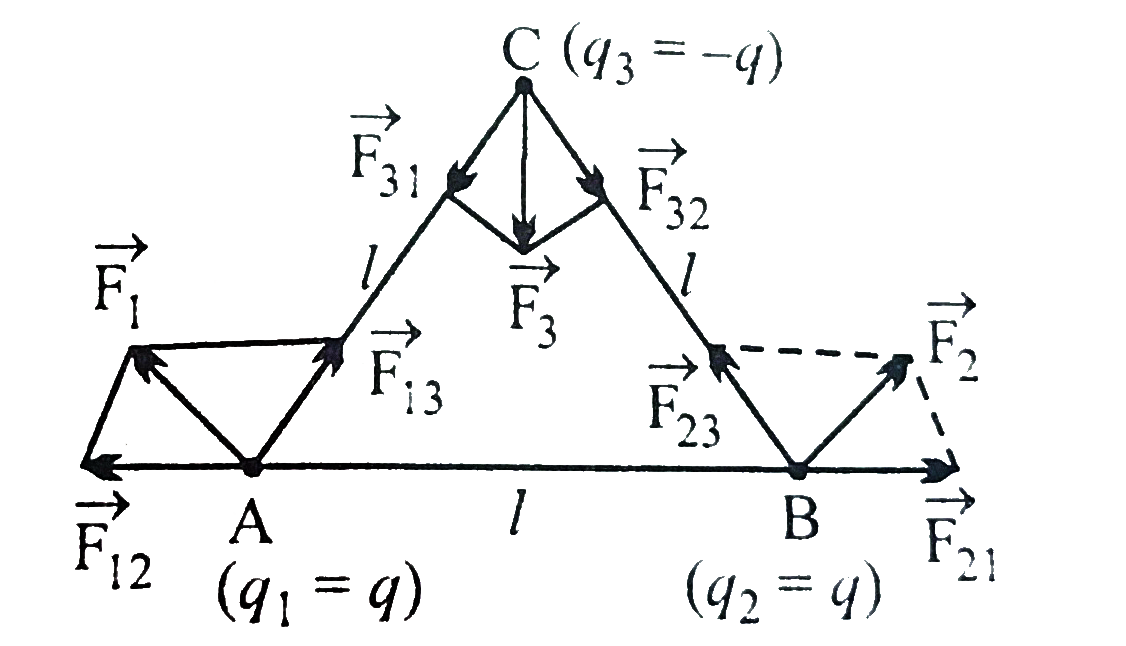 09:11View Solution
09:11View Solutionदो समान आवेशों Q को मिलाने वाली रेखा के केंद्र पर एक आवेश q रखा गया है । सिद्ध कीजिए की तीनो आवेश का यह निकाय संतुलन में होगा यदि `q=- (Q)/(4)` |
04:54View Solution`3xx10^(3)` न्यूटन प्रति कूलॉम में विधुत क्षेत्र में स्थित प्रोटॉन पर लगने वाले बल की गणना कीजिए ।
01:43View Solution`4muC ` आवेश नीरवत में स्थित है । उससे 2 मीटर की दुरी पर स्थित किसी बिंदु पर विधुत क्षेत्र की गणना कीजिए ।
01:39View Solutionक्या `0 *01 ` मीटर त्रिज्या के धात्विय गोले को 1 कूलॉम आवेश दिया जा सकता है ? वायु की परावैद्युत क्षमता `3xx 10 ^(6 )` न्यूटन प्रति कूलॉम है।
03:36View Solutionएक हीलियम नाभिक के कारण उससे `1 Å` की दुरी पर विधुत क्षेत्र की गणना कीजिए ।
06:24View Solution`+9e ` तथा `+e ` दो बिंदु आवेश एक-दूसरे से 8 मीटर की गुरी पर रखे गए है । तीसरा बिंदु आवेश q उपयुक्त दोनों आवेशों को मिलाने वाली रेखा पर कहाँ रखा जाये कि वह संतुलन में हो ?
06:10View Solution`1 *6 ` ग्राम के सिक्के से कितने इलेक्ट्रॉन निकले जाये की वह सिक्का उर्ध्वार्धर ऊपर की निर्दिष्ट `10 ^(9 )` न्यूटन प्रति कूलॉम के विद्युत क्षेत्र में ठीक तेर सके ?
04:34View Solutionकोई इलेक्ट्रॉन `2 *0 xx 10 ^(4 )NC ^(-1 )` परिमाण के एकसमान विधुत क्षेत्र में `1 *5 ` सेमी दुरी तक गिरता है । क्षेत्र का परिमाण समान रखते हुए इसकी दिशा उत्क्रमित कर दी जाती है तथा अब कोई प्रोटॉन उस क्षेत्र में उतनी ही दुरी तक गिरता है दोनों प्रकरणों में लगने वाले समय की गणना कीजिए । इस परिस्थति की' गुरुत्व के अधीन मुक्त पतन' से तुलना कीजिए।
 10:08View Solution
10:08View Solution`+5mu C ` और `-5muC ` के दो आवेश एक-दूसरे 1 मिमी कि दुरी पर स्थित है । द्विधुत आघूर्ण कि गणना कीजिए ।
01:33View Solution`5muC ` और `-5muC ` के दो बिंदु आवेश एक-दूसरे से 4 सेमी कि दुरी पर स्थित है । इस द्विधुत के मध्य बिंदु से 4 सेमी कि दुरी पर अक्षीय स्थिति में विधुत क्षेत्र के परिमाण कि गणना कीजिए ।
05:41View Solution`+1muC ` और `-1muC ` के दो बिंदु आवेश एक-दूसरे से 10 सेमी कि दुरी पर स्थित है । द्विध्रुव के मध्य बिंदु से 12 सेमी कि दुरी पर निरक्षीय स्थिति में विधुत क्षेत्र में परिमाण कि गणना कीजिए ।
05:47View Solutionदो आवेश `pm10muC ` एक-दूसरे से 5 मिमी दूर स्थित है । स्थिति में विधुत क्षेत्र कि गणना कीजिए-
द्विधुव के केंद्र से 15 सेमी कि दुरी पर धनावेश की और 15 सेमी की दुति पर अक्षीय स्थिति में ।04:57View Solutionदो आवेश `pm10muC ` एक-दूसरे से 5 मिमी दूर स्थित है । स्थिति में विधुत क्षेत्र कि गणना कीजिए-
द्विध्रुव के केंद्र से 15 सेमी की दुरी पर निरक्षीय स्थिति में ।04:04View Solutionजब एक वैधुत द्विध्रुव को `10 ^(4 )` न्यूटन/कूलॉम के एकसम्मान विधुत क्षेत्र में उसके सापेक्ष `30 ^(@)` के कोण पर रखा जाता है,तो वह `9 xx 10 ^(-26 )` न्यूटन मीटर के बल आघूर्ण का अनुभव करता है । इस वैधुत द्विधुत के आघूर्ण का परिमाण ज्ञात कीजिए ।
02:00View Solution2 सेमी द्विध्रुव लम्बाई का एक वैधुत द्विध्रुव `10 ^(5 )` न्यूटन/कूलॉम में एकसमान विधुत क्षेत्र में उसके सापेक्ष `60 ^(@)` के कोण पर रखस गया है। यदि वह `8 sqrt3 ` न्यूटन मीटर का बल आघूर्ण अनुभव करता है, तो गणना कीजिए-
वैधुत द्विध्रुव में आवेश का परिमाण ।02:32View Solution2 सेमी द्विध्रुव लम्बाई का एक वैधुत द्विध्रुव `10 ^(5 )` न्यूटन/कूलॉम में एकसमान विधुत क्षेत्र में उसके सापेक्ष `60 ^(@)` के कोण पर रखस गया है। यदि वह `8 sqrt3 ` न्यूटन मीटर का बल आघूर्ण अनुभव करता है, तो गणना कीजिए-
द्विध्रुव की स्थितिज ऊर्जा । यदि इसमें ± 4 n C का आवेश हो ।02:22View Solution`2xx 10^(-8)Cm` द्विध्रुव आघूर्ण वाले वैधुत द्विध्रुव को `10 ^(3 )NC ^(-1 )` तीव्रता के विधुत क्षेत्र में अस्थायी संतुलन की स्थिति में स्थायी संतुलन की स्थति में घुमाया जाता है । किए गए कार्य की गणना कीजिए ।
02:39View Solutionएक वैधुत द्विध्रुव की लम्बाई 2 सेमी है । जब इसे एकसमान विधुत क्षेत्र के साथ `60 ^(@)` का कोण बनाते हुए रखा जाता है तो यह `8 sqrt3 Nm ` के बल आघूर्ण का अनुभव करता है । द्विध्रुव की स्थितिज ऊर्जा की गणना कीजिए, यदि इसमें `pm 4n C ` का आवेश हो ।
03:16View Solutionएक विधुत क्षेत्र `( 3hati+ 2hatj+ 4hatk)` के द्वारा व्यक्त किया जाता है। XY तल में स्थित 5 मात्रक क्षेत्रफल से गुजरने वाले वैधुत फ्लक्स की गणना कीजिए।
03:54View Solutionएकसमान आवेशित अनंत लम्बे तार से 4 सेमी की दुरी पर विधुत क्षेत्र का परिमाण `9xx10^(4)` न्यूटन/ कूलॉम है। तार पर रेखिक आवेश घनत्व की गणना कीजिए।
04:05View Solution8 सेमी त्रिज्या के धातु के एक खोखले गोले को 20μCका आवेश दिया जाता है। विधुत क्षेत्र की गणना कीजिए -
गोले के केंद्र में 20 सेमी की दुरी पर।01:58View Solutionकूलॉम का आवेश दिया जाता है। स्थिति में विधुत क्षेत्र की गणना कीजिए -
गोले के पृष्ठ पर।01:52View Solution2 × 10 − 7कूलॉम का आवेश दिया जाता है। स्थिति में विधुत क्षेत्र की गणना कीजिए -
15 सेंटीमीटर त्रिज्या का गोले के केंद्र से 10 सेमी की दुरी पर।02:22View Solutionएकसमान आवेशित अनंत समतल चादर पर पृष्ठ आवेश घनत्व `5 xx 10 ^(-6 )` कूलॉम/"मीटर"^(2 )`है। इसके निकट `1 muC ` आवेश से आवेशित एक कण स्थित ह। उनके बिच लगने वाले बल की गणना कीजिए।
03:25View Solutionएक बिंदु आवेश के कारण गोलीय गाऊसीय पृष्ठ से - `3xx 10 ^(4) N m^(2) //C` का वैधुत फ्लक्स गुजरता है-
बिंदु आवेश की गणना कीजिए।01:45View Solutionएक बिंदु आवेश के कारण गोलीय गाऊसीय पृष्ठ से - `3xx 10 ^(4) N m^(2) //C` का वैधुत फ्लक्स गुजरता है-
यदि गाऊसीय पृष्ठ की त्रिज्या दुगुनी कर दी जाए तो पृष्ठ से कितने वैधुत फ्लक्स गुजरेंगे ?03:05View Solution2.5m व्यास का एक चालक गोला एक समान आवेशित ह। उस पर आवेश पृष्ठ घनत्व `100 mu C //m ^(2)` है। आवेश की गणना कीजिए -
गोले पर आवेश03:18View Solution2.5m व्यास का एक चालक गोला एक समान आवेशित ह। उस पर आवेश पृष्ठ घनत्व `100 mu C //m ^(2)` है। गणना कीजिए -
गोले से गुजरने वाला संपूर्ण वैधुत फ्लक्स।05:06View Solutionएकसमान विधुत क्षेत्र `vecE = 5xx 10 ^(3) hati N//C` दिया गया है। 10 सेमी भुजा का एक वर्ग YZ तल के समांतर रेखा। है। दिए गए क्षेत्र के कारण इस वर्ग से गुजरने वाले फ्लक्स की गणना कीजिए। यदि समतल X -अक्ष के साथ `30 ^(@)` का कोण बनाता है तो अब उसकी वर्ग से गुजरने वाला वैधुत फ्लक्स कितना होगा?
06:30View Solutionचित्र में विधुत क्षेत्र अवयव `E _(x) =ax ^(1/2), E _(y)= E_(z)=0` है जिसमे `alpha = 800 N//Cm ^(1/2)` है।
(a) गहन से गुजरने वाला फ्लक्स तथा
(b) गहन के भीतर आवेश परिकलित कीजिए `(a = 0.1m` मानिए। )
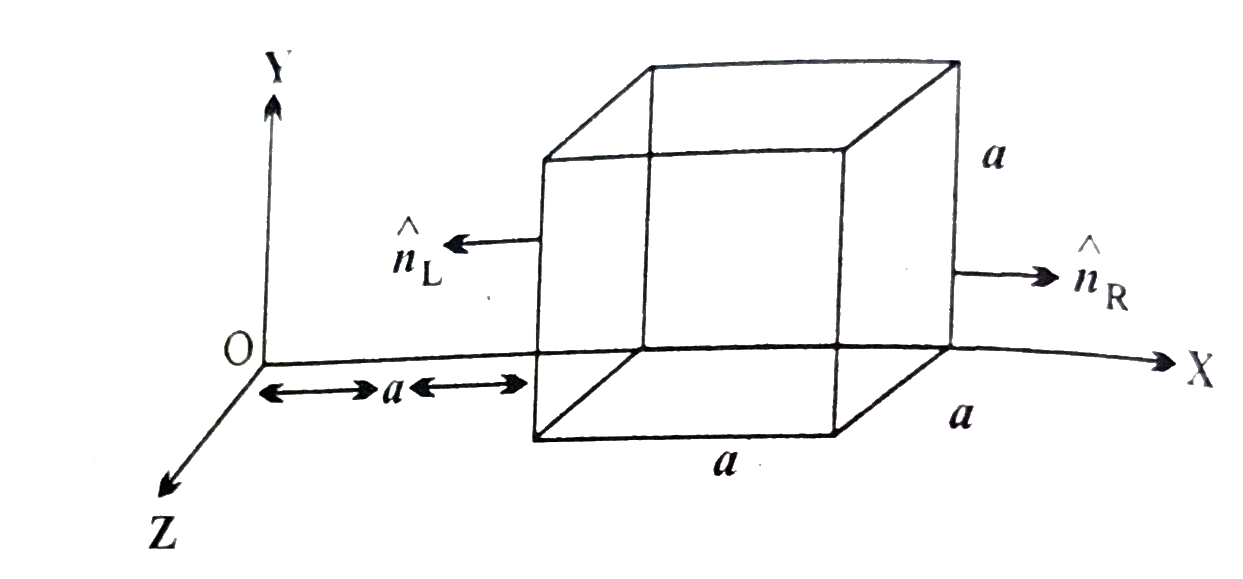 09:36View Solution
09:36View Solutionकोई विधुत क्षेत्र धनात्मक x के लिए घनात्मक X -दिशा में एकसमान है तथा उसी परिमाण के साथ परन्तु त्राणात्मक x के लिए त्राणात्मक x -दिशा में एकसमान है। यह दिया गया है कि `vecE = 200 hati N//C` जबकि `x gt 0` तथा `vecE=- 200 hati N//C`जबकि ` x lt 0|20` सेमी लम्बे तथा 5 सेमी त्रिज्या के किसी लंबवृत्तिया सिलिंडर का केंद्र मूलबिंदु पर तथा इसका अक्ष X -अक्ष के अनुदिश इस प्रकार है कि इसका एक फलक चित्र में दर्शाए अनुसार ` x =+10 ` सेमी पर है तथा दूसरा फलक `x =-10 ` सेमी पर है।
प्रत्येक फलक से गुजरने वाला नेट बहिमुर्खी कितना है ?05:52View Solutionकोई विधुत क्षेत्र धनात्मक x के लिए घनात्मक X -दिशा में एकसमान है तथा उसी परिमाण के साथ परन्तु त्राणात्मक x के लिए त्राणात्मक x -दिशा में एकसमान है। यह दिया गया है कि `vecE = 200 hati N//C` जबकि `x gt 0` तथा `vecE=- 200 hati N//C`जबकि ` x lt 0|20` सेमी लम्बे तथा 5 सेमी त्रिज्या के किसी लंबवृत्तिया सिलिंडर का केंद्र मूलबिंदु पर तथा इसका अक्ष X -अक्ष के अनुदिश इस प्रकार है कि इसका एक फलक चित्र में दर्शाए अनुसार ` x =+10 ` सेमी पर है तथा दूसरा फलक `x =-10 ` सेमी पर है।
सिलिंडर के पार्शव से गुजरने वाला फ्लक्स कितना है ?05:24View Solutionकोई विधुत क्षेत्र धनात्मक x के लिए घनात्मक X -दिशा में एकसमान है तथा उसी परिमाण के साथ परन्तु त्राणात्मक x के लिए त्राणात्मक x -दिशा में एकसमान है। यह दिया गया है कि `vecE = 200 hati N//C` जबकि `x gt 0` तथा `vecE=- 200 hati N//C`जबकि ` x lt 0|20` सेमी लम्बे तथा 5 सेमी त्रिज्या के किसी लंबवृत्तिया सिलिंडर का केंद्र मूलबिंदु पर तथा इसका अक्ष X -अक्ष के अनुदिश इस प्रकार है कि इसका एक फलक चित्र में दर्शाए अनुसार ` x =+10 ` सेमी पर है तथा दूसरा फलक `x =-10 ` सेमी पर है।
सिलिंडर से गुजरने वाला नेट बहिमुर्खी फ्लक्स कितना है ?06:28View Solutionकोई विधुत क्षेत्र धनात्मक x के लिए घनात्मक X -दिशा में एकसमान है तथा उसी परिमाण के साथ परन्तु त्राणात्मक x के लिए त्राणात्मक x -दिशा में एकसमान है। यह दिया गया है कि `vecE = 200 hati N//C` जबकि `x gt 0` तथा `vecE=- 200 hati N//C`जबकि ` x lt 0|20` सेमी लम्बे तथा 5 सेमी त्रिज्या के किसी लंबवृत्तिया सिलिंडर का केंद्र मूलबिंदु पर तथा इसका अक्ष X -अक्ष के अनुदिश इस प्रकार है कि इसका एक फलक चित्र में दर्शाए अनुसार ` x =+10 ` सेमी पर है तथा दूसरा फलक `x =-10 ` सेमी पर है।
सिलिंडर के भीतर नेट आवेश कितना है ?
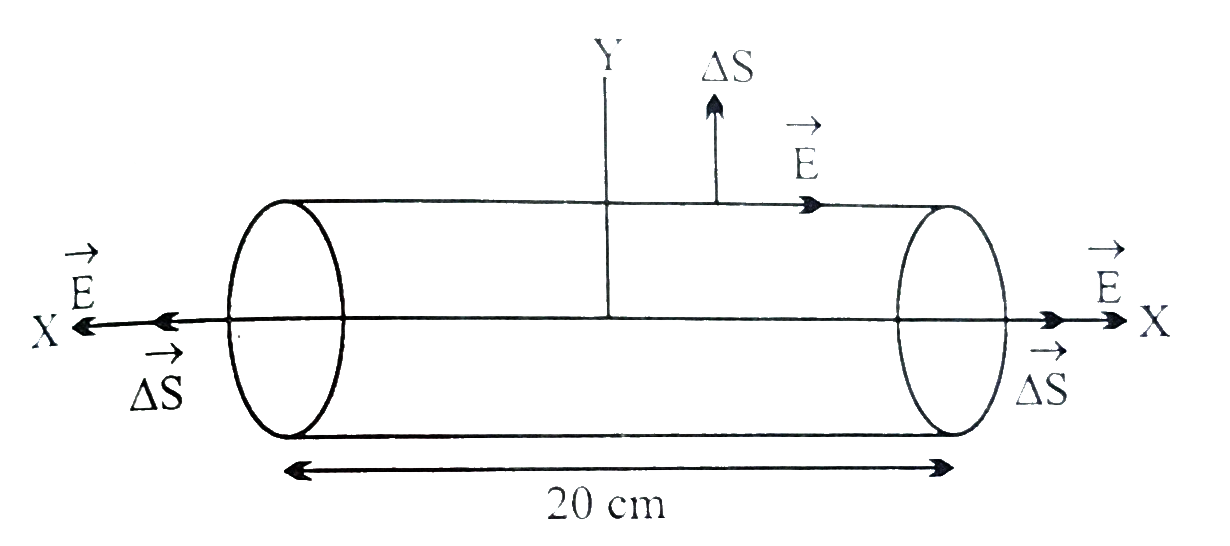 09:21View Solution
09:21View Solution
आंकिक उदाहरण questions and complete solutions for chapter वैधुत आवेश और क्षेत्र of NAVBODH PHYSICS (HINDI) of Class 12
All Exercises from NAVBODH PARIKSHA SAAR Class 12 PHYSICS वैधुत आवेश और क्षेत्र
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- अभ्यासार्थ प्रश्न (बहुविकल्पीय प्रश्न)
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न)
- अभ्यासार्थ प्रश्न (आंकिक प्रश्न)
- अभ्यासार्थ प्रश्न (उचित सम्बन्ध जोड़िए)
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न)
- अभ्यासार्थ प्रश्न (मूल्य अधारित प्रश्न)
- अभ्यासार्थ प्रश्न (रिक्त स्थानों की पूर्ति कीजिए)
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न प्लस)
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न)
- अभ्यासार्थ प्रश्न (सत्य/असत्य)
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न प्लस
- उदाहरण
- बहुविकल्पीय प्रश्न प्लस
- बोधात्मक प्रश्न प्लस
