Complete Solutions to बहुविकल्पीय प्रश्न प्लस of chapter वैधुत आवेश और क्षेत्र of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | वैधुत आवेश और क्षेत्र |
| NAVBODH PARIKSHA SAAR | बहुविकल्पीय प्रश्न प्लस |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
एक आवेश q को L लम्बाई के घन के केंद्र O पर रखा गया है। एकसमान आवेश q केंद्र O से L दुरी पर रखा गया है। फलक ABCD से गुजरने वाला वैधुत फ्लक्स होगा -
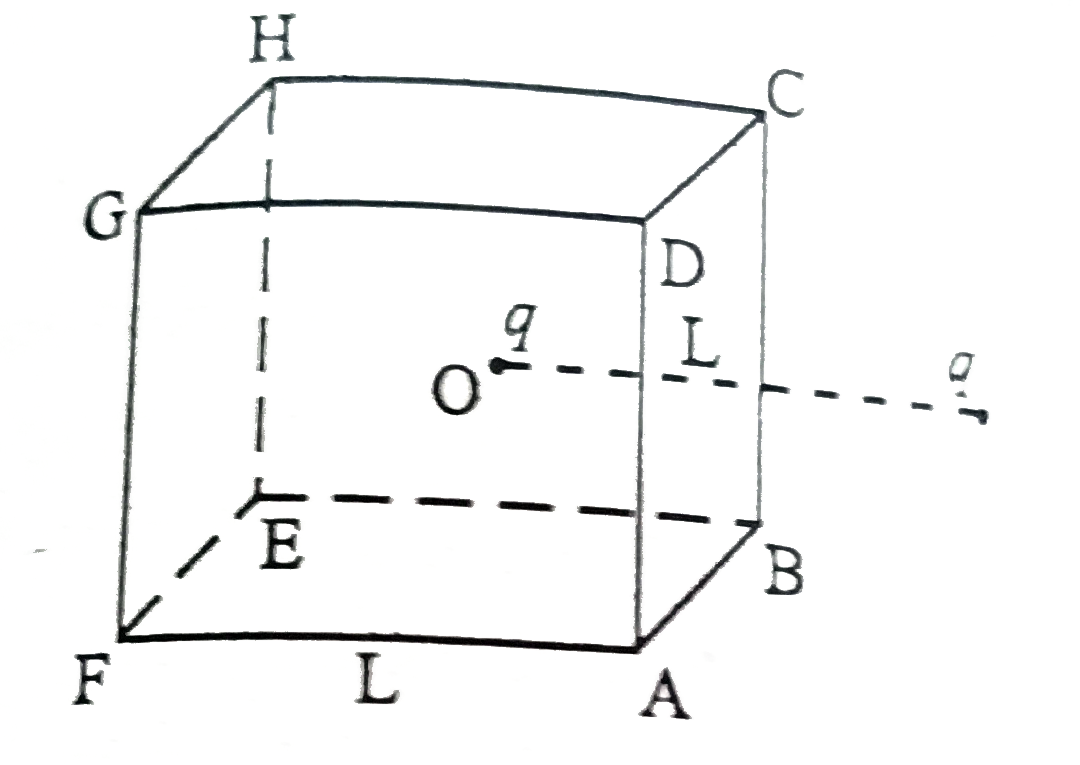 02:12View Solution
02:12View Solutionएक आवेश q को दो समान आवेशों Q को जोड़ने वाली रेखा के केंद्र पर इस प्रकार रखा जाता है की सम्पूर्ण निकाय साम्यावस्था में रहे। q का मान है -
02:45View Solutionतीन आवेश `-q _(1), + q _(2)` व `-q _(3)` चित्र के अनुसार रखे गए है। `-q _(1 )` पर लगने वाला बल निम्न के अनुक्रमानुपाती होगा -
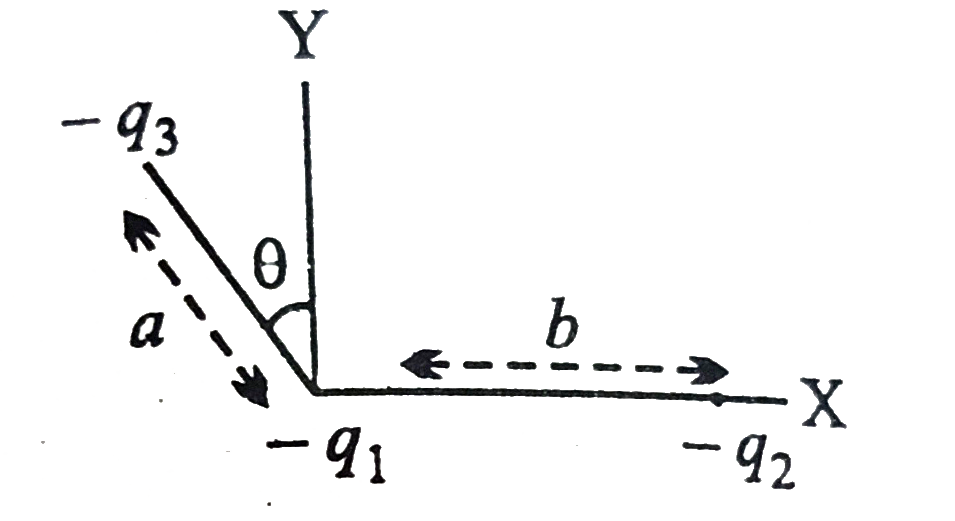 03:11View Solution
03:11View Solutionसामान त्रिज्याओं के लिए गोलाकार चालको पर आवेश की समान मात्रा है। उन्हें कुछ दुरी पर रखे पर उनके बीच प्रतिकर्षण बल F कार्य करता है। उतनी ही त्रिज्या वाले एक अन्य अनावेशित चालक का संपर्क पहले B से कराते है और फिर C से संपर्क कराकर उसे हटा दिया जाता है। B और C के बीच लगने वाला बल कुल कितना होगा-
04:58View Solutionचार आवेश जिसमे प्रत्येक का परिमाण -Q है किसी वर्ग के चार शीर्षो पर रखे है तथा इसके केंद्र पर कोई आवेश q स्थित है। यदि समस्त निकाय समयवस्था में है, तो q का मान है -
10:45View Solution`3 xx 10 ^(4 )` वोल्ट/मीटर में किसी एकसमान विधुत क्षेत्र में एक आवेशित तेल बून्द इस प्रकार नीलमबीत है की न तो निचे गिर सकती है और न ही ऊपर जा सकती है। ऐसे में तेल बून्द पर आवेश होगा (बूँद का द्रव्यमान `9.9 xx 10 ^( -15)` किग्रा तथा `g =10 "मीटर/सेकंड"^( 2 )` -
03:06View Solutionकोई आवेशित गेंद B किसी सिल्क की डोरी S से लटकी है जो आरेख में दर्शाए अनुसार किसी बड़ी आवेशित सहित P के साथ `theta ` कोण बनती है। शीट का पृष्ठ आवेश घनत्व `sigma ` किसके अनुक्रमानुपाती है-
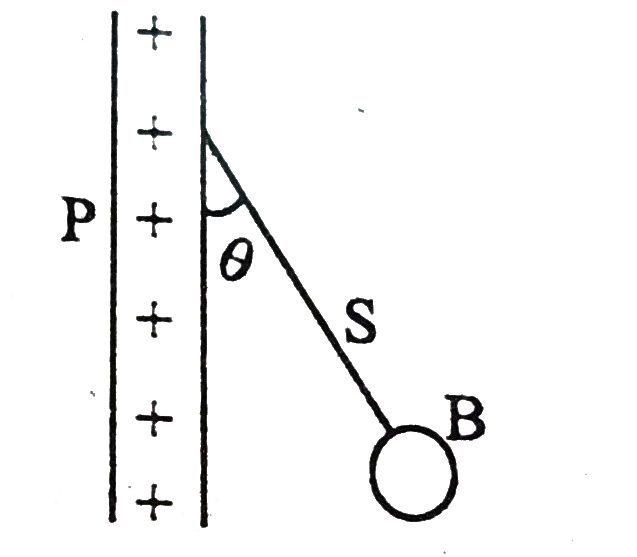 04:51View Solution
04:51View Solution`+8q ` और `-2q ` के दो बिंदु आवेश क्रमश: `x =0 ` तथा `x =L ` पर स्थति है। X -अक्ष पर उस बिंदु की स्थिति जहां पर इन दोनों आवेशों के कारन नेट विधुत क्षेत्र शून्य है , क्या होगा -
04:07View Solutionकिसी आसमान विधुत क्षेत्र से `30 ^(@)` के कोण पर एक वैधुत द्विध्रव रखस हुआ है। द्विध्रुव अनुभव करेगा -
03:41View SolutionR त्रिज्या पतले गोलीय कोश की सतह पर आवेश Q समान रूप से वितरित है। निम्नलिखित में से कोण-सा ग्राफ इस कोश द्वारा क्षेत्र `0lerltoo ` में उत्पन्न विधुत क्षेत्र E (r ) प्रदर्शित करेगा -
04:18View Solutionत्रिज्या R और कुल आवेश Q वाले एक ठोस गोले पर आवेश घनत्व वितरण `rho (r) = (Q)/(pi R ^(4)).r` से दिया जाता है गोले के केंद्र से `r _(1 )` दुरी पर गोले के अंदर एक बिंदु पर विधुत क्षेत्र की तीव्रता होगी -
05:45View Solutionत्रिज्या r की एक अर्धवृत्तीय वलय पर धनात्मक आवेश q समान रूप से वितरित है। केंद्र O पर परिणामी क्षेत्र `vecE ` है -
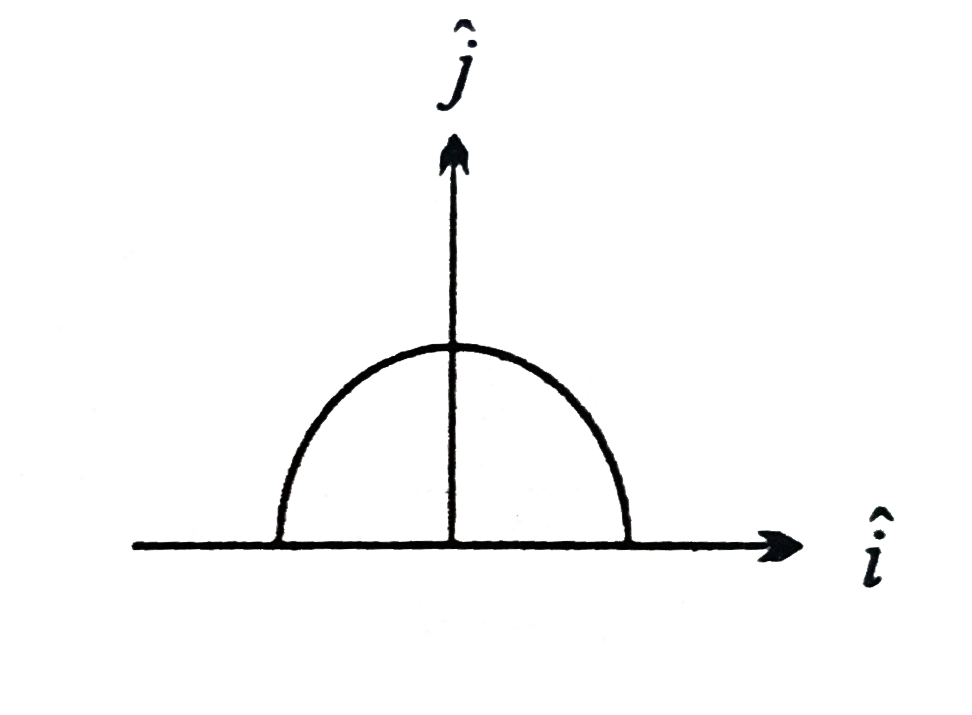 10:12View Solution
10:12View Solutionलंबाई l के दो द्रव्यमानहीन डोरियों द्वारा एक उभयनिष्ठ बिंदु से दो एकसमान आवेशित गोले लटकाये गए है , जो की प्रारमभ में दुरी `d ( d lt lt l)` पर अपने अन्योन्य विकर्षण के कारण है। दोनों गोलों से ावश एक स्थिर डॉ से लिक होना प्रारम्भ करता है। इसके परिणामस्वरूप आवेश एक दूसरे की और v वेग से गति करना प्रारम्भ करते है। तब दोनों के बिच दुरी x के फलन के रूप में है -
09:42View Solutionp द्विध्रुव आघूर्ण वाले वैधुत द्विध्रुव के लंबवत विभाजक रेखा पर एक बिंदु Q है। यदि बिंदु Q की द्विध्रुव से दुरी r द्विध्रुव के आकार की तुलना में बहुत अधिक हो तो बिंदु Q पर विधुत क्षेत्र अनुक्रमानुपाती होगा -
04:21View Solutionm द्रव्यमान तथा q आवेश का एक कण विधुत क्षेत्र E में विरामावस्था में है। यदि कण को छोड़ दिया जाये तो y दुरी तय करने के कण द्वारा प्राप्त गतिज ऊर्जा होगी -
02:19View Solutionएक खोखले विलगित चालक गोले को `10muC ` का धनवेश दिया जाता है। यदि गोले की त्रिज्या 2 मीटर हो तो गोले के केंद्र पर विधुत क्षेत्र होगा -
02:15View Solutionएक निश्चित दुरी पर स्थित दो आवेशों के बिच क परवैधुतांक वाला माध्यम भर दिया जाता है तो आवेशों के बिच लगने वाला अधिकतम बल -
03:33View Solutionएक आवेशित तार को a त्रिज्या के अर्धवृत्ताकार चाप के रूप में मोड़ दिया जाता है। यदि प्रति मीटर लंबाई पर आवेश `lamda ` कूलॉम/मीटर हो तो इसके केंद्र पर विधुत क्षेत्र होगा -
05:34View Solutionएक आवेश q और घन के कोने पर रखा है। घन के कोने से होकर जाने वाला वैधुत फ्लक्स है -
02:16View Solutionq माइक्रो कूलॉम का एक आवेश `0.1` मीटर भुजा के घन के केंद्र पर रखा है। घन के प्रत्येक पृष्ठ से निकलने वाला वैधुत फ्लक्स है-
02:04View Solutionद्विध्रुव आघूर्ण `vecp ` का एक वैधुत द्विध्रुव एकसमान चुम्बकीय क्षेत्र `vecB ` में सतत ह। इस पर कार्य करने वाला बल आघूर्ण है -
05:47View Solutionएक आवेश q एक घन के केंद्र पर स्थित है तो घन के किसी भी पृष्ठ से आने वाला वैधुत फ्लक्स होगा -
02:32View Solutionएक इलेक्ट्रॉन हाइड्रोजन नाभिक के चारों और r त्रिज्या के वृताकार पथ पर घूम रहा है। इन दोनों के बीच कूलॉम बल `vecF` है- ( जहाँ `k=1/(4piin_0)`)
05:07View Solutionएक वैधुत द्विध्रुव के आवेश का परिमाण q तथा द्विध्रुव आघूर्ण p है। यह एकसमान विधुत क्षेत्र E में रखा है। यदि इसका द्विध्रुव आघूर्ण क्षेत्र की डिश में हो तब इस पर कार्यरत बल तथा स्थितिज ऊर्जा क्रमश: है -
03:05View Solutionनिर्वात की विधुतशीलता `epsi _(0 )` का मात्रक है-
01:33View Solutionदो आवेश `q _(1 )` और `q _(2 ),30 ` सेमि की दुरी पर चित्रानुसार स्थित है। एक तीसरे आवेश `q _(3 )` को 40 सेमि त्रिज्या के वृत्त के चाप के अनहदिश C से D तक चलाया जाता है। की स्थितिज ऊर्जा में परिवर्तन `(q_(3))/(4 pi epsi _(0))` है। k का मान होगा -
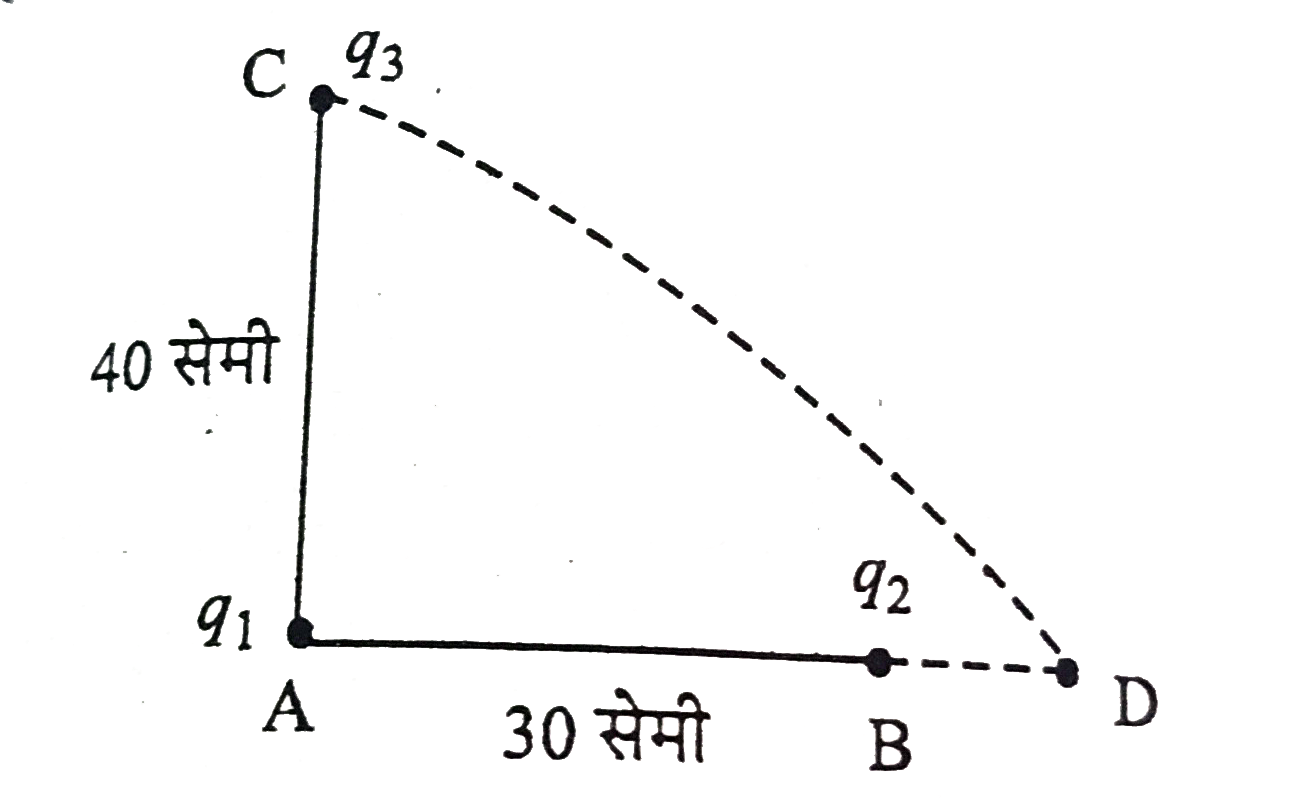 07:31View Solution
07:31View Solution`vecp ` आघूर्ण का एक वैधुत द्विध्रुव अचर वैधुत क्षेत्र ` vecE ` के साथ पड़ा है। इस द्विध्रुव `90 ^(@)` से घूमने में किया गया कार्य होगा -
02:15View SolutionL मीटर भुजा का एक वर्गाकार तल कागज़ पृष्ठ में स्थित है। कागज पृष्ठ में क्रियाकारी एक अचर विधुत क्षेत्र `vecE ` (वोल्ट/मीटर) चित्र में दर्शाए अनुसार वर्गीय तल के केवल निचले अर्ध भाग में सिमित है। तल से सम्बद्ध वैधुत फ्लक्स SI मात्रक में होगा -
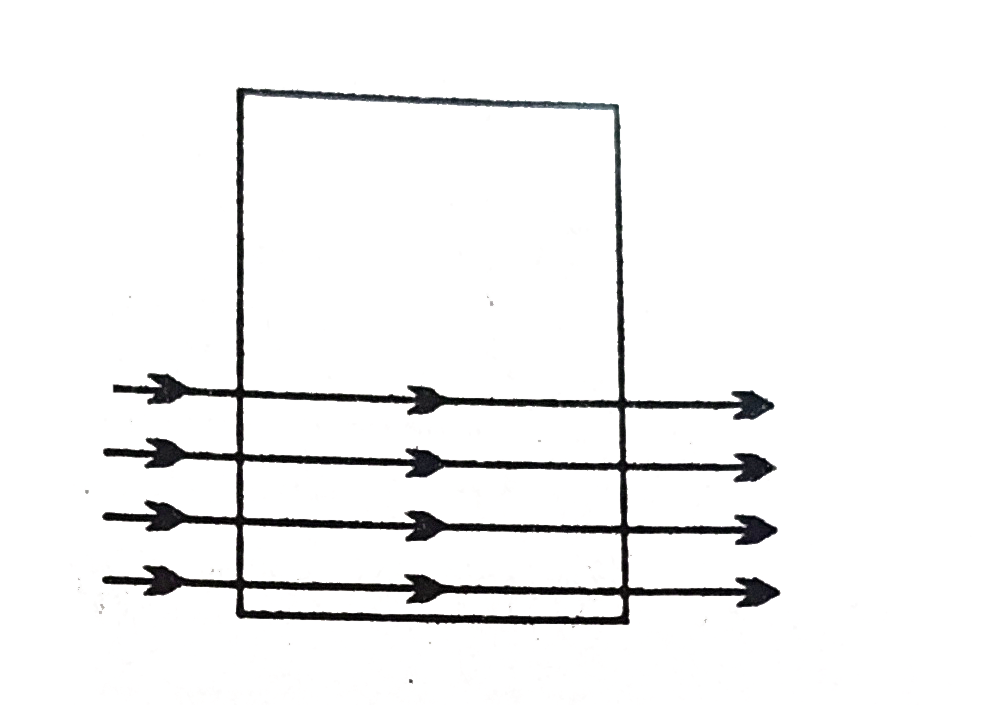 02:38View Solution
02:38View Solutionतीन बिंदु आवेशों `+q , -2q ` और `+q ` को क्रमानुसार विन्दुओ `(0,a,0), (0,0,0)` और `(a, 0,0)` पर रखा गया है। इस आवेश व्यवस्था के लिए वैधुत द्विध्रुव आघूर्ण सदिश के मान और दिशा क्रमानुसार होंगे -
05:00View Solutionएक खोखले गोले के भीतर q कूलॉम का आवेश स्थित है। यदि चित्रानुसार वक़्र्तल B से सम्बद्ध वैधुत फ्लक्स वोल्ट मीटर में `phi ` हो, तो समतल तल A से सम्बद्ध वोल्ट मीटर में वैधुत फ्लक्स होगा -
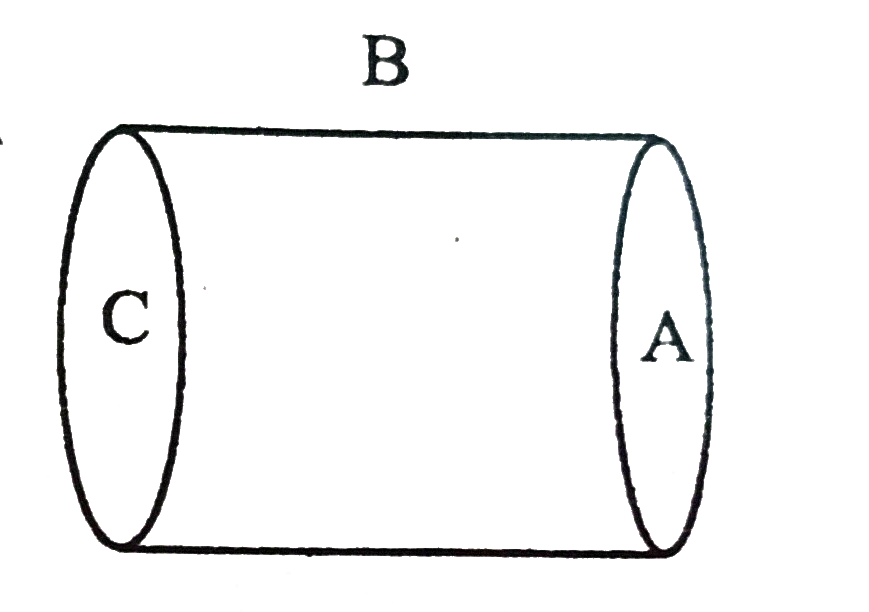 04:14View Solution
04:14View Solutionचित्रानुसार दो आवेश +q और -q क्रमशः बिंदु A और B पर स्थति है। उनके बीच की दुरी २ल है। A और B का बिंदु C है। एक अन्य आवेश +Q को CRD अर्ध वृत्त पर चलाने में किया गया कार्य होगा -
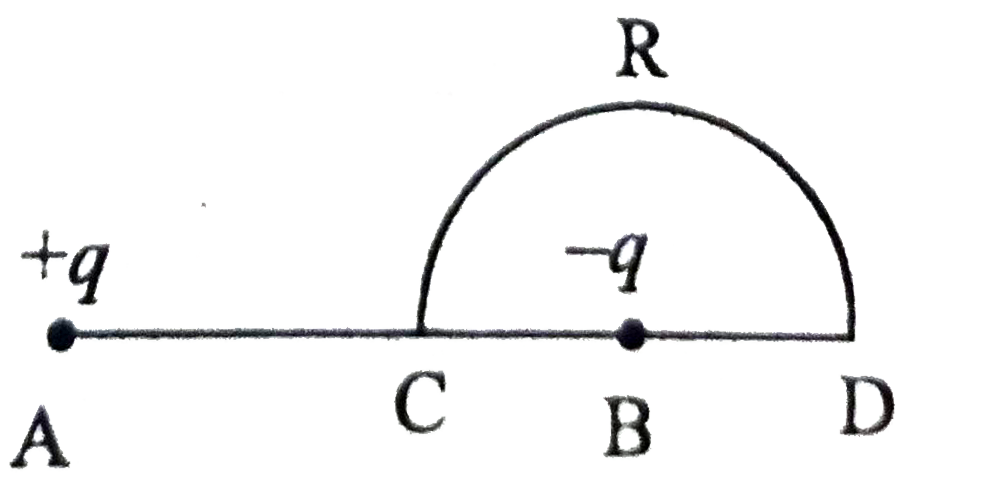 05:06View Solution
05:06View Solutionएक पतली विधुत चालक R त्रिज्या की रंग (छल्ला) को +Q आवेश दिया गया है। रिंग के केंद्र O पर रिंग के भाग AKB के कारन विधुत क्षेत्र का मान E है। रिंग के शेष भाग ACBD के आवेश के कारण केंद्र O पर विधुत क्षेत्र का मान होगा -
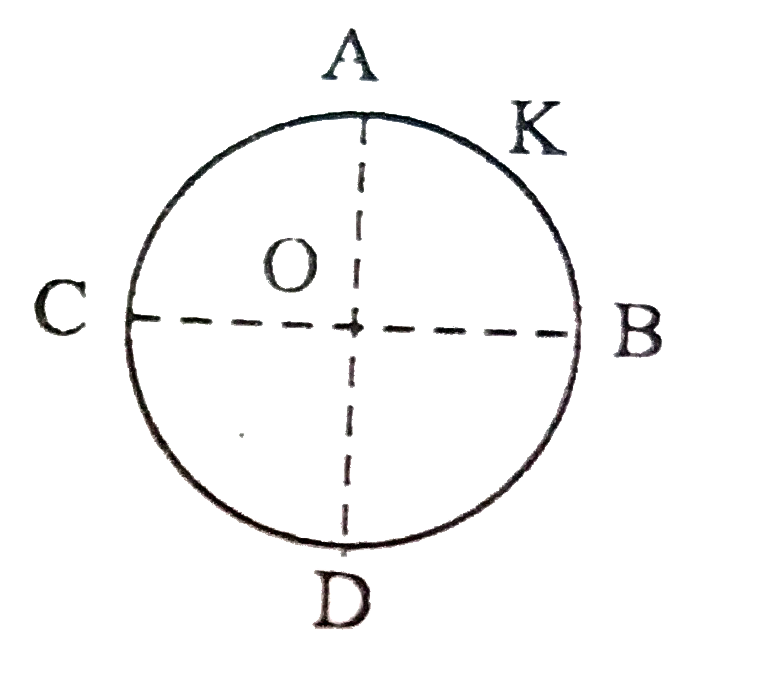 04:41View Solution
04:41View SolutionL मीटर भुजा का एक वर्गाकार तल कागज पृष्ठ में स्थति है। कागज पृष्ठ में एकसमान विधुत क्षेत्र E (वोल्ट/मीटर) उसी स्थान पर वर्ग की उर्ध्वार्धर भुजा के मध्य चित्र में दर्शये अनुसार `theta ` कोण बनाते हुए कार्य करता है। पृष्ठ से सम्बद्ध वैधुत फ्लक्स वोल्ट मीटर में होगा-
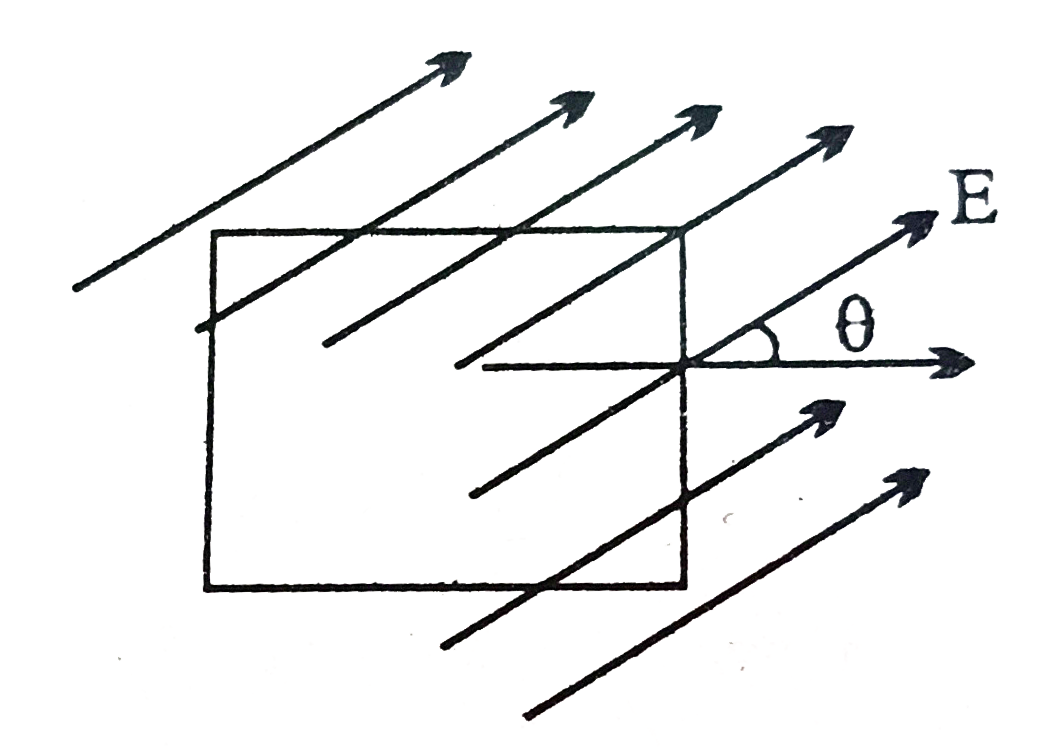 02:44View Solution
02:44View Solutionधातु की दो समान्तर प्लैटे मिनमे +Q और - Q आवेश है, कुछ दुरी पर स्थित है। यदि अब प्लेटो को केरोसिन तेल की टंकी में डुबो दिया जाये तो उनके बीच विधुत क्षेत्र की तीव्रता -
03:06View Solutionएक आवेशित चालक गोलीय कवच (कोश) के केंद्र से `(3R )/(2 )` दुरी पर विधुत क्षेत्र E है, जहां R गोलीय कवच की त्रिज्या है। इस गोलीय कवच के उसके केंद्र से `R //2 ` दुरी पर विधुत क्षेत्र होगा -
02:35View Solutionएक आवेश Q और R त्रिज्या के गैसीय गोले से परिबद्ध है। यदि त्रिज्या दोगुनी हो जाये तो बाह्य वैधुत फ्लक्स -
02:25View Solutionएक गोलीय सममित आवेश वितरण दिया गया है जसमे आवेश घनत्व इस प्रकार परिवर्तित होता है-
`rho (r) = rho _(0) ((5)/(4) - (r)/(R)), r =R` तक तथा `rho (r) =0, r gt R` के लिए, जहां r मूलबिंदु से दुरी है। मिलबिंदु से दुरी `r (rltR )` पर विधुत क्षेत्र इस प्रकार दिया जाता है -10:41View Solutionदो एकसमान आवेशित गोलों को बराबर लम्बाई की डोरियों से लटकाया गया है। डोरियाँ परस्पर `30^@` कोण बनाती हैं। जब `0.8 g cm^(-3)` घनत्व के द्रव में लटकाया जाता हैं, तब भी वही कोण रहता है। यदि गोले के पदार्थ का घनत्व `1.6 g cm^(-3)` है तब द्रव का परावैद्युतांक ज्ञात कीजिए।
14:59View Solutionp द्विध्रुव आघूर्ण का एक वैधुत द्विध्रुव E तीव्रता के विधुत क्षेत्र में रखा जाता है। यह द्विध्रुव ऐसी स्थिति प्राप्त कर लेता है जिसमे इसका अक्ष क्षेत्र की दिशा से `theta ` कोण बनाता है माना `theta = 90 ^(@)` पर द्विध्रुव की स्थितिज ऊर्जा शून्य है। द्विध्रुव पर बल आघूर्ण तथा स्थितिज ऊर्जा क्रमश: होंगे -
07:34View Solutionत्रिज्या R के एकसमान आवेशित (कुल आवेश =q ) कुचालक गोले के कारन विधुत क्षेत्र E का गोले के केंद्र से दुरी r के साथ विचरण का ग्राफ होगा -
03:11View Solutionमुक्त आकाश के लिए परावैधुतांक `epsi _(0 )` का विमीय सूत्र है -
02:23View SolutionX -अक्ष पर `x =-a ` तथा `x =a ` पर दो समान आवेश, प्रत्येक q रखे जाते है। मूलबिंदु पर m द्रव्यमान तथा `q _(0 ) = q /2 ` आवेश का कण रहा जाता है। यदि कण को Y -अक्ष के अनुदिश थोड़ा - सा विस्थापन `y (yltlta )` कर दिया जाए तो कण पर लगने वला बल अनुक्रमानुपाती होगा -
09:26View Solutionकिसी बल क्षेत्र में कण की स्थतिज ऊर्जा है -
`U = (A)/( r ^(2) )-(B)/(r)`
जहाँ A तथा B धनात्मक नियतांक तथा r कण की बल क्षेत्र के केंद्र से दुरी है। स्थायी संतुलन की दिशा में कण की दुरी है -02:09View Solutionयदि भुजा a के किसी घन के एक कोने पर बिंदु आवेश q रखा जाए तो इससे गुजरने वाला फ्लक्स होगा -
02:14View Solutionदो सरकंडे की गोलियाँ जिन पर समान आवेश है , समान लंबाई की डोरियों से एक ही बिंदु से लटकाई गई है। साम्यावस्था में उनके बीच की दुरी r है। अब डोरियों को दृढ़तापूर्वक आधी ऊँची पर बाँध देते है। साम्यावस्था में उनके बीच की दुरी होगी -
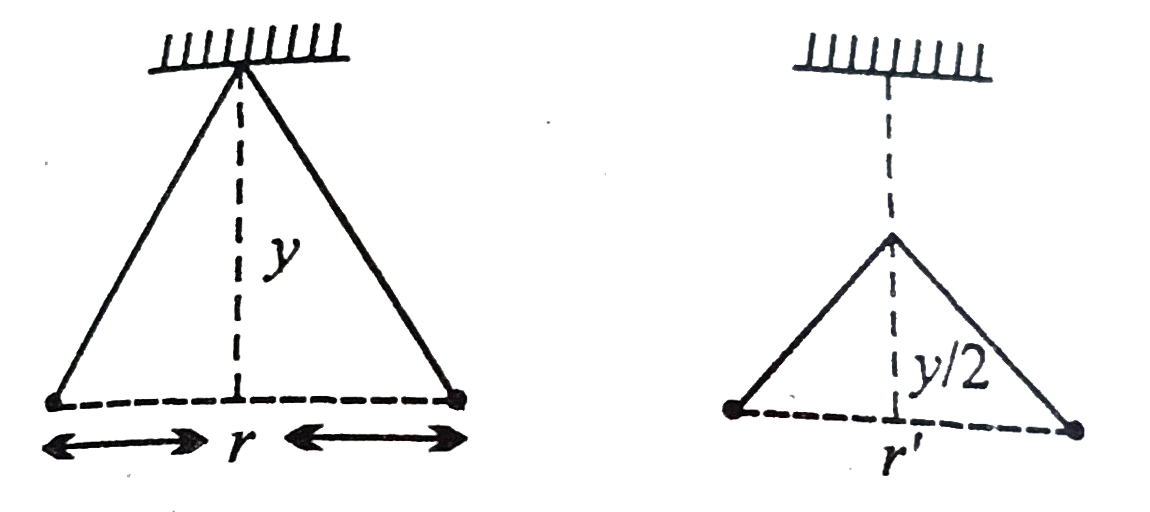 08:50View Solution
08:50View Solutionएक वैधुत द्विध्रुव को `2xx10 ^(5 )` न्यूटन/कूलॉम तीव्रता के विधुत क्षेत्र में `30 ^(@)` कोण पर रखने से उस पर 4 न्यूटन/मीटर का बल आघूर्ण लगता है। यदि द्विधुव की लंबाई 2 सेमी हो, तो उस पर आवेश होगा -
03:04View Solutionकल्पना कीजिए की एक प्रोटोन और एक इलेक्ट्रॉन के आवेश में अलप अंतर होता है। इनमे से एक -e तथा दुस्र्र `e + Delta e ` है। यदि एक-दूसरे से d दुरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के आकार से बहुत अधिक है) स्थिरवैधुत बल और गुरुत्वीय बल का परिणामी शून्य हो तो `Delta e ` की कोटि होगी-
(दिया है : हाइड्रोजन का द्रव्यमान `m _(h ) = 1.67 xx 10 ^(-27)` किग्रा)05:26View Solutionत्रिज्या a और b के दो सकेंद्रिय गोलों के बीच के स्थान में आयतन आवेश घनत्व `rho = A/r` है जहाँ A स्थिरांक तथा r केंद्र से दुरी है। गोलों के केंद्र पर एक बिंदु आवेश Q है। A का वह मान, जिससे गोलों के बीच के स्थान में विधुत क्षेत्र एकसमान हो, होगा -
09:08View Solutionएक वैधुत द्विध्रुव का स्तर द्विध्रुव आघूर्ण `vecp ` है , जो की X -अक्ष से `theta ` कोण बनाता है। विधुत क्षेत्र `vecE _(1 ) = E hati ` में रखने पर यह बल आघूर्ण `vec tau _(i )=tauhatk ` का अनुभव करता है। विधुत क्षेत्र `vecE_(2) = sqrt 3 E_(1)hatJ` में रखने पर यह बल आघूर्ण `vec tau _(2) =-vec tau _(1)` का अनुभव करता है कोण `theta ` का मान होगा -
03:40View Solution
बहुविकल्पीय प्रश्न प्लस questions and complete solutions for chapter वैधुत आवेश और क्षेत्र of NAVBODH PHYSICS (HINDI) of Class 12
All Exercises from NAVBODH PARIKSHA SAAR Class 12 PHYSICS वैधुत आवेश और क्षेत्र
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- अभ्यासार्थ प्रश्न (बहुविकल्पीय प्रश्न)
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न)
- अभ्यासार्थ प्रश्न (आंकिक प्रश्न)
- अभ्यासार्थ प्रश्न (उचित सम्बन्ध जोड़िए)
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न)
- अभ्यासार्थ प्रश्न (मूल्य अधारित प्रश्न)
- अभ्यासार्थ प्रश्न (रिक्त स्थानों की पूर्ति कीजिए)
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न प्लस)
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न)
- अभ्यासार्थ प्रश्न (सत्य/असत्य)
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न प्लस
- उदाहरण
- बहुविकल्पीय प्रश्न प्लस
- बोधात्मक प्रश्न प्लस
