Complete Solutions to Exercise of chapter NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEI |
| NCERT | Exercise |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
(a) Two stable isotope of `._3Li^6` and `._3Li^7` have respective abundances of `7.5%` and `92.5%`. These isotopes have masses 6.01512 and 7.01600 u respectively. Find the atomic weight of lithium.
(b) Boron has two stable isotopes `._5B^(10)` and `._5B^(11)`. Their respective masses are 10.01294 u and 11.00931 u, and the atomic weight of boron is 10.81 u. Find the abundances of `._5B^(10)` and `._5B^(11)`.
View SolutionThe three stable isotopes of neon `._10Ne^(20), ._10Ne^(21)` and `._10Ne^(22)` have respective abundances of `90.51%,0.27%` and `9.22%`. The atomic masses of the three isotopes are `19.99u, 20.99u` and `21.99u` respectively. Obtain the average atomic mass of neon.
View SolutionObtain the binding energy (in MeV) of a nitrogen nucleus `(""_(7)^(14)N)` , given `m(""_(7)^(14)N)`
`=14.00307" "u`
View SolutionObtain the binding energy of the nuclei `._26Fe^(56)` and `._83Bi^(209)` in units of MeV from the following data: `m(._26Fe^(56))=55.934939a.m.u.` , `m=(._83Bi^(209))=208.980388 a m u`. Which nucleus has greater binding energy per nucleon? Take `1a.m.u =931.5MeV`
View SolutionA given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separated all the neutrons and protons form each other. for simplicity, assume that the coin is entirely made of `._29Cu^(63)` atoms (of mass 62.92960 u).
View SolutionWrite nuclear reaction equation for
(i) `alpha` decay of `._88Ra^(226)` (ii) `alpha` decay of `._94Pu^(242)` (iii) `beta^(-)` decay of `._15P^(32)`
(iv) `beta^(-)` decay of `._83Bi^(210)` (v) `beta^(+)` decay of `._6C^(11)` (vi) `beta^(+)` decay of `._43Tc^(97)`
(vii) Electron capture of `._54Xe^(120)`.
View SolutionA radioactive isotope has a life of T years. How long will it take the activity to reduce to (a) `3.125% (b) 1%` of its original activity?
View SolutionThe normal activity of living carbon -containing matter is found to be about 15 decay per minute for every gram of carbon. This activity arises form the small proportion of radioactive `._6C^(14)` present with the ordinary `._6C^(12)` isotope. When the organism is dead, its interaction with the atmosphere which maintains the above equilibrium activity, ceases and its activity begins to drop. from the known half life (=5730years) of `._6C^(14)`, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of `._6C^(14)` dating used in archaeology. Suppose a specimen from Mohenjo - daro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus Valley Civilization.
View SolutionObtain the amount of `.^60Co` necessary to provide a radioactive source of `8.0 Ci` strength. The half-life of `.^60Co` is `5.3` years?
View SolutionThe half life of `._38Sr^(90)` is 28 years. What is disintegration rate of 15g of this isotope?
View SolutionObtain approx. the ratio of the nuclear radii of the gold isotope `._79Au^(197)` and silver isotope `._47Ag^(107)`.
View SolutionConsider the following nuclear fission reaction
`._(88)Ra^(226) to ._(86)Rn^(222)+._(2)He^(4)+Q`
In the fission reaction. Kinetic energy of `alpha`-particle is 4.44 MeV. Find the energy emitted as `gamma`-radiation in keV in this reaction.
`m(._(88)Ra^(226))=226.005` amu
`m(._(86)Rn^(222))=222.000` amu
View SolutionThe radionuclide `._6C^(11)` decays according to `._6C^(11)to ._5B^(11) +e^(+) +v`: half life =20.3min. The maximum energy of the emitted positron is `0.960 MeV`. Given the mass values
`m(._6C^(11))=11.011434u, m(._6B^(11))=11.009305u`
Calculate Q and compare it with maximum energy of positron emitted.
View SolutionThe nucleus `.^(23)Ne` deacays by `beta`-emission into the nucleus `.^(23)Na`. Write down the `beta`-decay equation and determine the maximum kinetic energy of the electrons emitted. Given,`(m(._(11)^(23)Ne) =22.994466 am u` and `m (._(11)^(23)Na =22.989770 am u`. Ignore the mass of antineuttino `(bar(v))`.
View SolutionThe Q value of a nuclear reaction
A+b=C+d is defined by `Q=[m_A+m_b-m_C-m_d]c^2` where the masses refer to the respective nuclei. Determine form the given data the Q value of the following reactions and state whether the reactions are exothermic of endothermic.
(i) `._1H^(1)+._1H^3to ._1H^2+._1H^2`
(ii) `._6C^(12)+._6C^(12) to ._10Ne^(20)+._2He^4`
Atomic masses are given to be
`m(._1H^2)=2.014102u , m(._1H^3)=3.016049 u, m(._6C^(12))=12.000000u , m(._10Ne^(20))=19.992439u`
View SolutionSuppose, we think of fission of a `._26Fe^(56)` nucleus into two equal fragments `._13Al^(28)`. Is the fission energetically possible? Argue by working out Q of the process. Given `m(._26Fe^(56))=55.93494u, m(._13Al^(28))=27.98191 u.`
View SolutionThe fission properties of `._84Pu^(239)` are very similar to those of `._92U^(235)`. The average energy released per fission is `180MeV`. How much energy in MeV is released if all the atoms in 1kg of pure `._94Pu^(239)` undergo fission.
View SolutionA 1000 MW fission reactor consumes half of its fuel in 5.00yr. How much `._92U^(235)` did it contain initially? Assume that the reactor operates `80%` of the time and that all the energy generated arises form the fission of `._92U^(235)` and that this nuclide is consumed by the fission process.
View SolutionHow long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? The fusion reaction can be taken as `._1H^2+._1H^2to ._1H^3+n+3.17MeV`
View SolutionCalculate the height of potential barrier for a head on collision of two deuterons. The effective radius of deuteron can be taken to be 2fm. Note that height of potential barrier is given by the Coulomb repulsion between two deuterons when they just touch each other.
View Solutionfrom the relation `R=R_0A^(1//3)`, where `R_0` is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A ).
View Solutionfor the `beta^(+)` (positron) emission from a nucleus, there is another competing process known as electron capture. Electron from an inner orbit (say K shell) is captured by the nucleus and neutrino is emitted. Show that if `beta^(+)` emission is energetically allowed, electron capture is necessarily allowed but not vice -versa.
View SolutionIn a periodic table, the average atomic mass of magnesium is given as `24.312 u`. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are `._12Mg^(24) (23.98504u)`, `._(12)Mg^(25) (24.98584)` and `._12Mg^(26) (25.98259 u)`. The natural abundance of `._12Mg^(24)` is `78.99%` by mass. Calculate the abundances of the other two isotopes.
View SolutionThe neutron separation energy is defined to be the energy required to remove a neutron form nucleus. Obtain the neutron separation energy of the nuclei `._(20)Ca^(41)` and `._(13)Al^(27)` from the following data : `m(._20Ca^(40))=39.962591u` and `m(._(20)Ca^(41))=40.962278u`
`m(._(13)Al^(26))=25.986895u` and `m(._(13)Al^(27))=26.981541u`
View SolutionA source contains two phosphorus radionuclides `._(15)P^(35) (T_(1//2)=14.3"days")` and `._(15)P^(33) (T_(1//2)=25.3"days")`. Initially, `10%` of the decays come from `._(15)P^(35)`. How long one must wait until `90%` do so?
View SolutionUnder certain circumstances, a nucleus can decay by emitting a particle more massive than an `alpha`-particle. Consider the following decay processes:
`._(88)Ra^(223)to._(82)Pb^(209)+._(6)C^(14)`, `._(88)Ra^(223)to._(86)Rn^(219)+._(2)He^(4)`
(a) Calculate the Q-values for these decays and determine that both are energetically allowed.
View SolutionConsider the fission `._(92)U^(238)` by fast neutrons. In one fission event, no neutrons are emitted and the final stable and products, after the beta decay of the primary fragments are `._(58)Ce^(140)` and `._(44)Ru^(99)`. Calculate Q for this fission process, The relevant atomic and particle masses are:
`m(._(92)U^(238))=238.05079u, m(._(58)Ce^(140))=139.90543 u, m(._(34)Ru^(99))=98.90594 u`
View SolutionConsider the so called D-T reaction (deuterium-tritium fusion) `._1H^2+._1H^3to._2He^4+n`
Calculate the energy released in MeV in this reaction from the data
`m(._1H^2)=2.014102u, m(._1H^3)=3.016049u`
(b) Consider the radius of both deuterium and tritium to be approximately 2.0fm. what is the kinetic energy needed to overcome the Coulomb repulsion between the two nuclei? To what temperature must the gases the be heated to initiate the reaction?
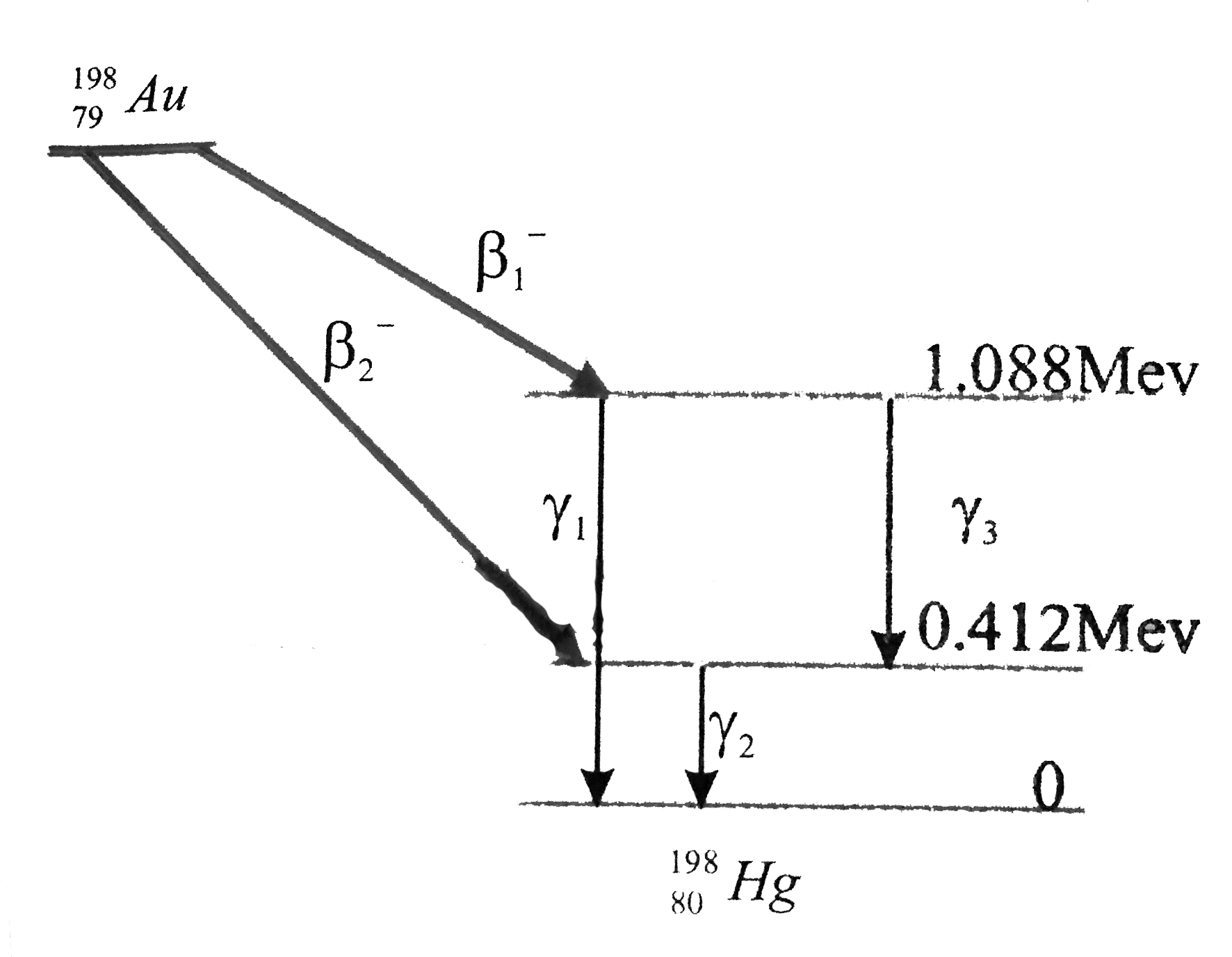
View SolutionObtain the maximum kinetic energy of `beta`-particles, and the radiation frequencies of `gamma` decays in the decay scheme shown in Fig. `14.6`. You are given that `m(.^(198)Au)=197.968233 u, m(.^(198)Hg)=197.966760 u`
View SolutionCalculate and compare the energy released by (a) fusion of 1.0kg of hydrogen deep within the sun, and (b) the fission of 1.0kg of `U^(235)` in a fission reactor.
View SolutionSuppose India has a target of producing by `2020 AD, 200,000 MW` of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an avedrage, the efficiency of utilization(i.e conversion to electric energy) of thermal energy produced in a reactor was `25%`. How much amount of fissionable uranium would our country need per year by `2020`? Take the heat energy per fission of `.^(235)U` to be about `200 MeV`.
View Solution
Exercise questions and complete solutions for chapter NUCLEI of NCERT PHYSICS(ENGLISH) of Class 12