Obtain the maximum kinetic energy of $β$ -particles, and the radiation frequencies of $γ$ decays in the decay scheme shown in Fig. $14.6$ . You are given that $m (.^{198} A u) = 197.968233 u, m (.^{198} H g) = 197.966760 u$

Video Solution

Text Solution

Verified by Experts

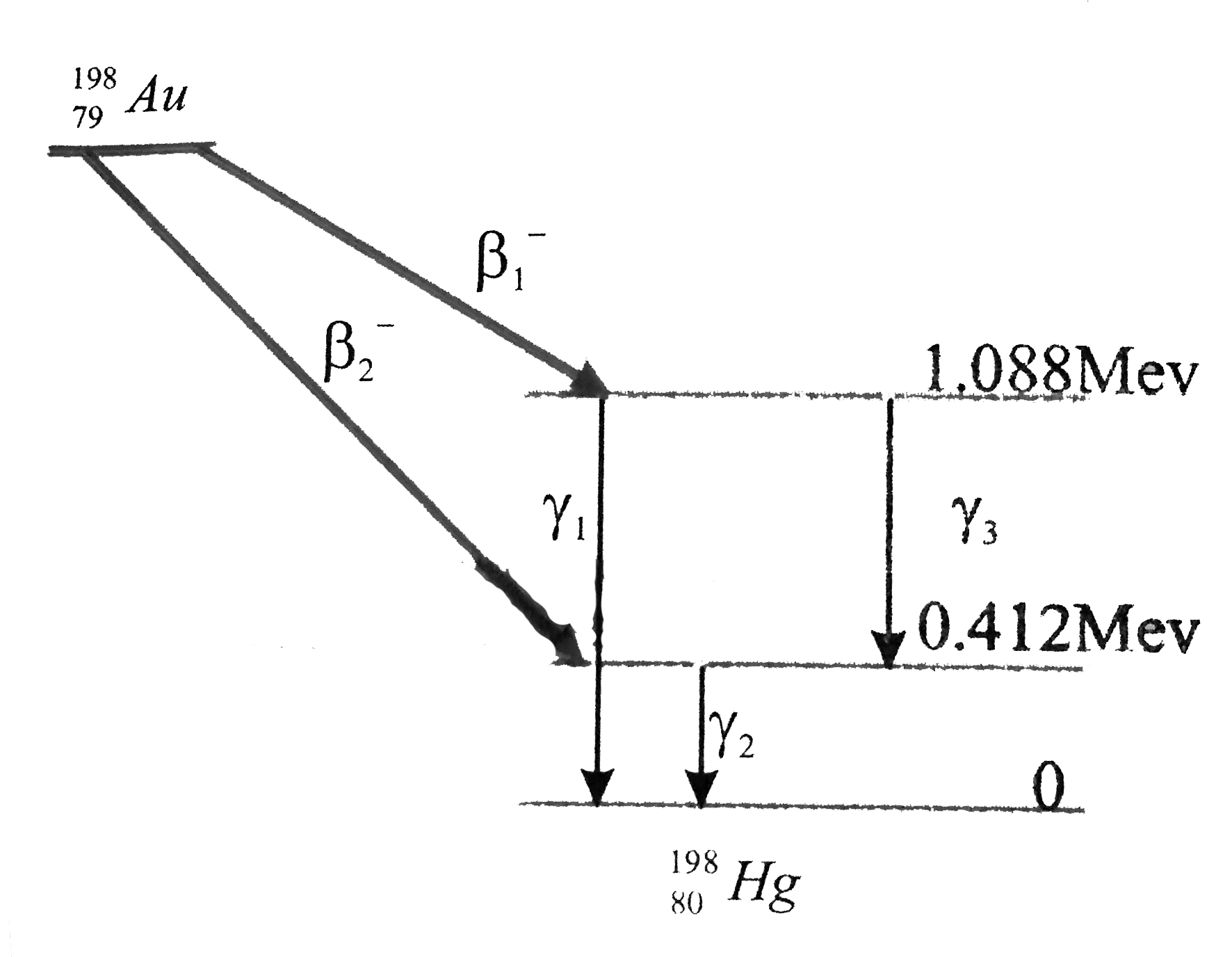
It can be observed from the given Y-decy diagram that $y_{1}$ decays from the 1.088 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to $y_{1}$ -decay is given as :
$E_{1}$ =1.088-0=1.088 MeV
$h v_{1} = 1.088 \times 1.6 \times 10^{- 19} \times 10^{6} J$
Where, h=Planck's constant $= 6.6 \times 10^{- 34} J s$
$v_{1}$ = Frequency of radiation radiated by $y_{1}$ -decay
$∴ v_{1} = \frac{E_{1}}{h}$
$= \frac{1.088 \times 1.6 \times 10^{- 19} \times 10^{6}}{6.6 \times 10^{- 34}} = 2.637 \times 10^{20} H z$
It can be observed form the given y-decay diagram that $y_{2}$ decays from the 0.412 MeV energy level to the 0MeV energy level.
Hence, the energy corresponding to $y_{2}$ -decay is given as:
$E_{2} = 0.412 - 0 = 0.412 M e V$
$h v_{2} = 0.412 \times 1.6 \times 10^{- 19} \times 10^{6} J$
Where,
$v_{2} =$ Frequency of radation radiated by $y_{2}$ - decay
$∴ v_{2} = \frac{E_{2}}{h}$
$= \frac{0.412 \times 1.6 \times 140^{- 19} \times 10^{6}}{6.6 \times 10^{- 34}} = 9.988 \times 10^{19} H z$
It can be observed form the given y-decay diagram that $y_{3}$ decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to $y_{3}$ -decay is given as :
$E_{3} = 1.088 - 0.412 = 0.676 M e V$
$h v_{3} = 0.676 \times 10^{- 19} \times 10^{6} J$
Where,
$v_{3}$ =Fequency of radiation radiated by $y_{3}$ -decay
$∴ v_{3} = \frac{E_{3}}{h}$
$= \frac{0.676 \times 1.6 \times 10^{- 19} \times 10^{6}}{6.6 \times 10^{- 34}} = 1.639 \times 10^{20} H z$
Mass of $m (_{78}^{198} A u) = 197.968233 u$
Mass of $m (_{80}^{198} H g) = 197.966760 u b$
$1 u = 931.5 M e V / c^{2}$
Energy of the highest level is given as :
$E = [m (_{78}^{198} A u) - m (_{80}^{190} H g)]$
$= 197.968233 - 197.966760 = 0.001473 u$
$= 0.001473 \times 931.5 = 1.372099 M e V$
$β_{1}$ decays from the 1.3720995 MeV level to the 1.088 MeV level
$∴$ Maximum kinetic energy of the $β_{1}$ particle =1.3720995-1.088 =0.2840995 MeV
$β_{2}$ decays from the 1.3720995 MeV level to the 0.412 MeV level
$∴$ Maximum kinetic energy of the $β_{2}$ particle=1.3720995-0.412=0.9600995 MeV

|

Updated on:21/07/2023

Class 12 PHYSICS NUCLEI

Topper's Solved these Questions

Similar Questions

NCERT ENGLISH-NUCLEI-Exercise

Home
Ask Doubt
Profile