Complete Solutions to प्रश्नावली (लघु उत्तरीय प्रश्न ) of chapter रैखिक प्रोग्रामन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | रैखिक प्रोग्रामन |
| NCERT EXEMPLAR HINDI | प्रश्नावली (लघु उत्तरीय प्रश्न ) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
व्यवरोधों `2x + y le 6, x le 2, x ge 0, y ge 0`. के अंतर्गत Z = 11x + 7y का अधिकतम मान निर्धारित कीजिए।
View Solutionव्यवरोधों `x+y le1, x ge 0,y ge 0`. के अंतर्गत Z = 3x+ 4y का अधिकतमीकरण कीजिए।
View Solutionव्यवरोधों `x le 3, y le 2, x ge 0,t ge 0` के अंतर्गत फलन Z = 11x + 7y का अधिकतमीकरण कीजिए।
View Solutionव्यवरोधों `x + y le 7, 2x - 3y + 6 ge 0, x ge 0, y ge 0` के अतंर्गत Z = 13x – 15y का न्यूनतमीकरण कीजिए।
View SolutionZ= 3x +4y का अधिकतम मान ज्ञात कीजिए, यदि LPP का सुसंगत क्षेत्र (छायांकित)आकृति में प्रदर्शित है।
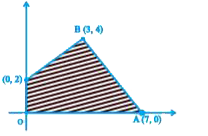
View Solutionकिसी LPP का सुसंगत क्षेत्र (छायांकित) आकृति में प्रदर्शित है। Z = 5x +7y का न्यूनतम मान ज्ञात कीजिए।
View Solutionकिसी LPP का सुसंगत क्षेत्र आकृति में प्रदर्शित है। Z = 11x +7y का न्यूनतम मान ज्ञात कीजिए।

View Solutionउपर्युक्त प्रश्न संख्या 7 पर ध्यान दीजिए। Z का अधिकतम मान ज्ञात कीजिए।
View Solutionकिसी LPP का सुसंगत क्षेत्र आकृति में प्रदर्शित है। इस क्षेत्र के प्रत्येक कोनीय बिंदु पर Z= 4x + y का मान निकालिए। Z का न्यूनतम मान ज्ञात कीजिए, यदि उसका अस्तित्व है।
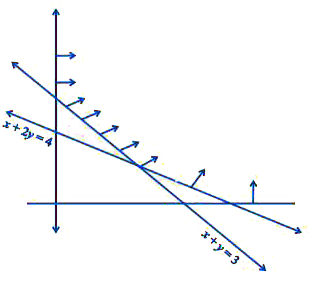
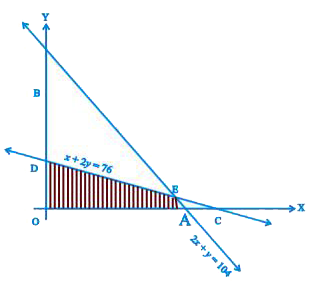
View Solutionआकृति में एक LPP का सुसंगत क्षेत्र (छायांकित) प्रदर्शित है। Z = x + 2y का अधिकतम तथा न्यूनतम मान निकालिए।
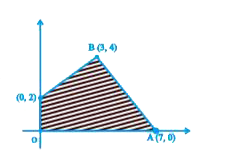
View Solutionएक इलेक्ट्रानिक परिपथ के निर्माता के पास 200 प्रतिरोधक (resistors), 120 ट्रांजिस्टर तथा 150 संधारित्र (capacitors) का स्टाक है तथा उसे A और B दो प्रकार के परिपथ का उत्पादन करना है। A प्रकार के परिपथ में 20 प्रतिरोधकों, 10 ट्रांजिस्टर तथा 10 संधारित्रों की आवश्यकता पड़ती है। B प्रकार के परिपथ में 10 प्रतिरोधकों, 20 ट्रांजिस्टरों तथा 30 संधारित्रों की आवश्यकता पड़ती है। यदि प्रत्येक A प्रकार के परिपथ पर लाभ 50 रु तथा प्रत्येक B प्रकार के परिपथ पर लाभ 60 रु होता है, तो इस समस्या का एक LPP के रूप में सूत्रण कीजिए ताकि निर्माता अपने लाभ का अधिकतमीकरण कर सके।
View Solutionएक फर्म को बड़ी वैनों, जिनमें से प्रत्येक 200 पैकेज तथा छोटी वैनों, जिनमें से प्रत्येक 80 पैकेज ढो सकती है के उपयोग द्वारा, 1200 पकेज ढोना है। प्रत्येक बड़ी वैन को लगाने पर 400 रु तथा प्रत्येक छोटी वैन को लगाने पर 200 रु खर्च होते हैं। इस कार्य के लिए 3000 रु से अधि क खर्च नहीं किए जा सकते हैं तथा बड़ी वैन की संख्या छोटी वैन की संख्या से अधिक नहीं हो सकती है। इस समस्या का एक LPP के रूप में सूत्रण कीजिए, यदि यह दिया हुआ है कि उद्देश्य कुल लागत का न्यूनतमीकरण करना है।
View Solutionएक कंपनी A तथा B, दो प्रकार के पेंचों का उत्पादन करती है। सभी पेंचों को एक चूड़ी डालने वाली मशीन तथा एक खाँचा मशीन से होकर गुजरना पड़ता है। A प्रकार के पेंचों के एक बक्स को चूड़ी डालने की मशीन के 2 मिनट प्रयोग की तथा खाँचा मशीन के प्रयोग की 3 मिनट की आवश्यकता पड़ती है। B प्रकार के पेंचों के एक बक्स को चूड़ी डालने की मशीन के प्रयोग की 8 मिनट तथा खाँचा मशीन के प्रयोग की 2 मिनट की आवश्यकता पड़ती है। प्रत्येक मशीन एक सप्ताह में 60 घंटे के लिए उपलब्ध है।
इन पेंचों को बेचने पर कंपनी को A प्रकार के पेंचों पर 100 रु प्रति बक्स तथा B प्रकार के पेंचों पर 170 रु प्रति बक्स लाभ प्राप्त होता है।
इस समस्या का एक LPP के रूप में सूत्रण कीजिए, दिया हुआ है कि उद्देश्य लाभ का अधि कतमीकरण करना है।
View Solutionएक कंपनी A तथा B दो प्रकार के स्वेटरों का उत्पादन करती है। A प्रकार के एक स्वेटर बनाने में 360 रु तथा B प्रकार के एक स्वेटर बनाने में 120 रु खर्च होते है। कंपनी प्रतिदिन अधिक से अधिक 300 स्वेटर बना सकती है तथा अधिकतम 72000 रु खर्च कर सकती है। B प्रकार के स्वेटरों की संख्या A प्रकार के स्वेटरों की संख्या से 100 से अधिक नहीं हो सकती है। प्रत्येक B प्रकार के स्वेटर पर 120 रु लाभ अर्जित करती है। कंपनी के कुल लाभ का अधिकतमीकरण करने के लिए इस समस्या का एक LPP के रूप में सूत्रण कीजिए।
View Solutionएक व्यक्ति अपनी मोटरसाइकिल को 50 `km//h` की रफ्तार से चलाता है। उसे पेट्रोल पर 2 रु प्रति किलोमीटर खर्च करने पड़ते हैं। यदि वह 80 `km//h` की तेज रफ्तार से चलाता है, तो पेट्रोल का खर्चबढ़ कर 3 रु प्रति किलोमीटर हो जाता है। उसके पास पेट्रोल पर खर्च करने के लिए अधि क से अधिक 120 रु है तथा 1 घंटे का समय है। वह, उस अधिकतम दूरी को ज्ञात करना चाहता है, जो वह तय कर सकता है।
इस समस्या को एक रैखिक प्रोग्रामन समस्या के रूप में व्यक्त कीजिए।
View Solution
प्रश्नावली (लघु उत्तरीय प्रश्न ) questions and complete solutions for chapter रैखिक प्रोग्रामन of NCERT EXEMPLAR HINDI of Class 12