Complete Solutions to उदाहरण of chapter रैखिक प्रोग्रामन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | रैखिक प्रोग्रामन |
| NCERT EXEMPLAR HINDI | उदाहरण |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
Z = 4x + 3y का अधिकतम मान निर्धारित कीजिए, यदि LPP का सुसंगत क्षेत्र आकृति में प्रदर्शित है।
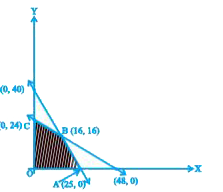
View SolutionZ = 3x + 2y का न्यूनतम मान (यदि कोई है) निर्धारित कीजिए, यदि LPP का सुसंगत क्षेत्र आकृति में प्रदर्शित किया गया है।

View Solutionनिम्नलिखित LPP को आरेखीय विधि से हल कीजिए:
Z= 2x +3y का, व्यवरोधों `x + y le 4, x ge 0, y ge 0` के अंतर्गत, अधिकतमीकरण कीजिए।
View Solutionएक निर्माण कंपनी दो प्रकार के टेलीविज़न सेट बनाती है। एक काला-सफेद तथा दूसरा रंगीन। कंपनी के पास प्रति सप्ताह अधिकतम 300 सेट तैयार करने के साधन हैं। एक काला-सफेद सेट बनाने में 1800 रु तथा एक रंगीन सेट बनाने में 2700 रु लगते हैं। कंपनी टेलीविज़न सेट बनाने में प्रति सप्ताह 648000 रु से अधिक खर्च नहीं कर सकती है। यदि कंपनी प्रत्येक काले-सफेद सेट पर 510 रु तथा प्रत्येक रंगीन सेट पर 675 रु का लाभ अर्जित करती है। तो प्रत्येक प्रकार के कितने सेट निर्मित किए जाने चाहिए, जिससे उसे अधिकतम लाभ हो इस समस्या का एक LPP के रूप में सूत्रण कीजिए, दिया हुआ है कि उद्देश्य लाभ का अधिकतमीकरण करना है।
View Solutionउदाहरण 4 पर ध्यान दीजिए। LPP को हल कीजिए।
View SolutionZ=3x +5y का नीचे दिए व्यवरोधों के अंतर्गत न्यूनतमीकरण कीजिए:
`x+2y ge 10`
`x+y ge 6`
`3x+ y ge 8`
`x, y ge 0`
View Solutionरैखिक व्यवरोधों के एक निकाय द्वारा निर्धारित, किसी सुसंगत क्षेत्र के कोनीय बिंदु (0, 10), (5, 5), (15, 15), (0, 20) हैं। मान लीजिए कि Z = px + qy, जहाँ `p, q ge 0`. p तथा q पर लगने वाला वह प्रतिबंध, जिससे Z का अधिकतम मान (15, 15) तथा (0, 20) दोनों ही बिंदुओं पर प्राप्त हो, तब
View Solutionकिसी LPP का सुसंगत क्षेत्र (छायांकित) आकृति में प्रदर्शित किया गया है। Z = 4x + 3y का न्यूनतम मान किस बिंदु पर होगा?
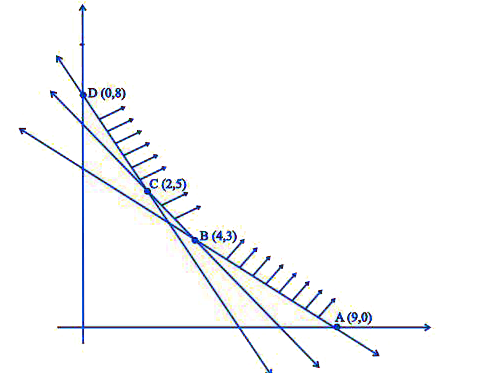
View Solutionकिसी LPP में, वह रैखिक फलन, जिसका अधिकतमीकरण या न्यूनतमीकरण करना होता है, एक रैखिक _________ फलन कहलाता है।
View Solutionकिसी LPP के सभी रैखिक व्यवरोधों द्वारा निर्धारित उभयनिष्ठ क्षेत्र एक _________ क्षेत्र कहलाता है।
View Solutionबतलाइए कि कथन सत्य हैं या असत्य-
यदि किसी रैखिक प्रोग्रामन समस्या का सुसंगत क्षेत्र (R) परिबद्ध है, तो उद्देश्य फलन Z = ax + by का R में अधिकतम तथा न्यूनतम दोनों ही मान होते हैं।
View Solutionबतलाइए कि कथन सत्य हैं या असत्य-
किसी रैखिक प्रोग्रामन समस्या के उद्देश्य फलन Z= ax + by का न्यूनतम मान सदैव किसी एक ही कोनीय बिंदु पर प्राप्त होता है।
View Solution
उदाहरण questions and complete solutions for chapter रैखिक प्रोग्रामन of NCERT EXEMPLAR HINDI of Class 12