Complete Solutions to Electric Charges And Field of chapter ELECTRIC CHARGES AND FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CHARGES AND FIELD |
| NCERT EXEMPLAR | Electric Charges And Field |
| Number Of Questions | 31 |
| Academic Year | 2023-24 |
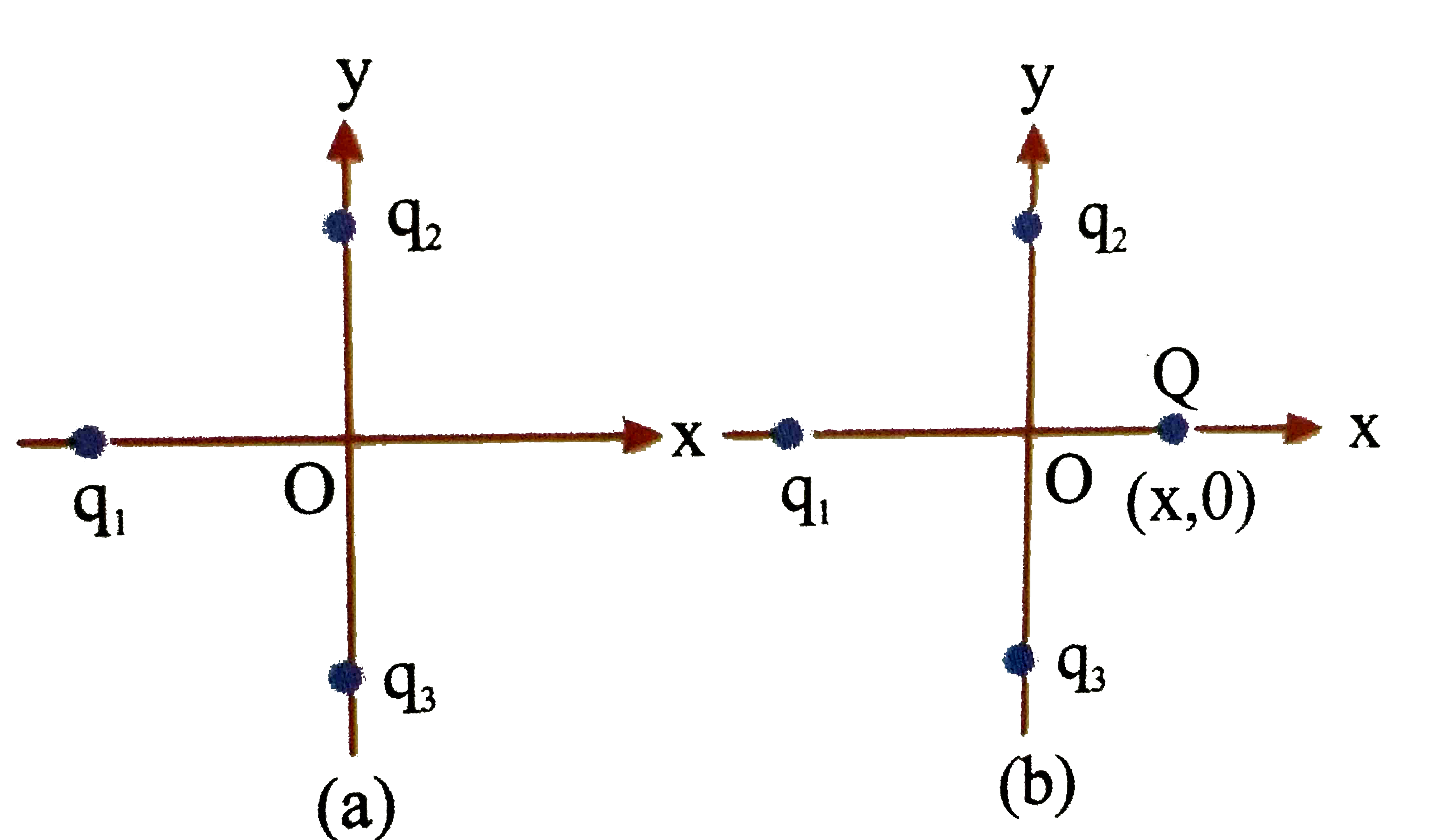
In figure two positive charges `q_(2)` and `q_(3)` fixed along the y-axis, exert a net electric force in the `+x` direction on a charge `q_(1)` fixed along the x-axis if a positive charge `Q` is added at `(x,0)` the force on `q_(1)`
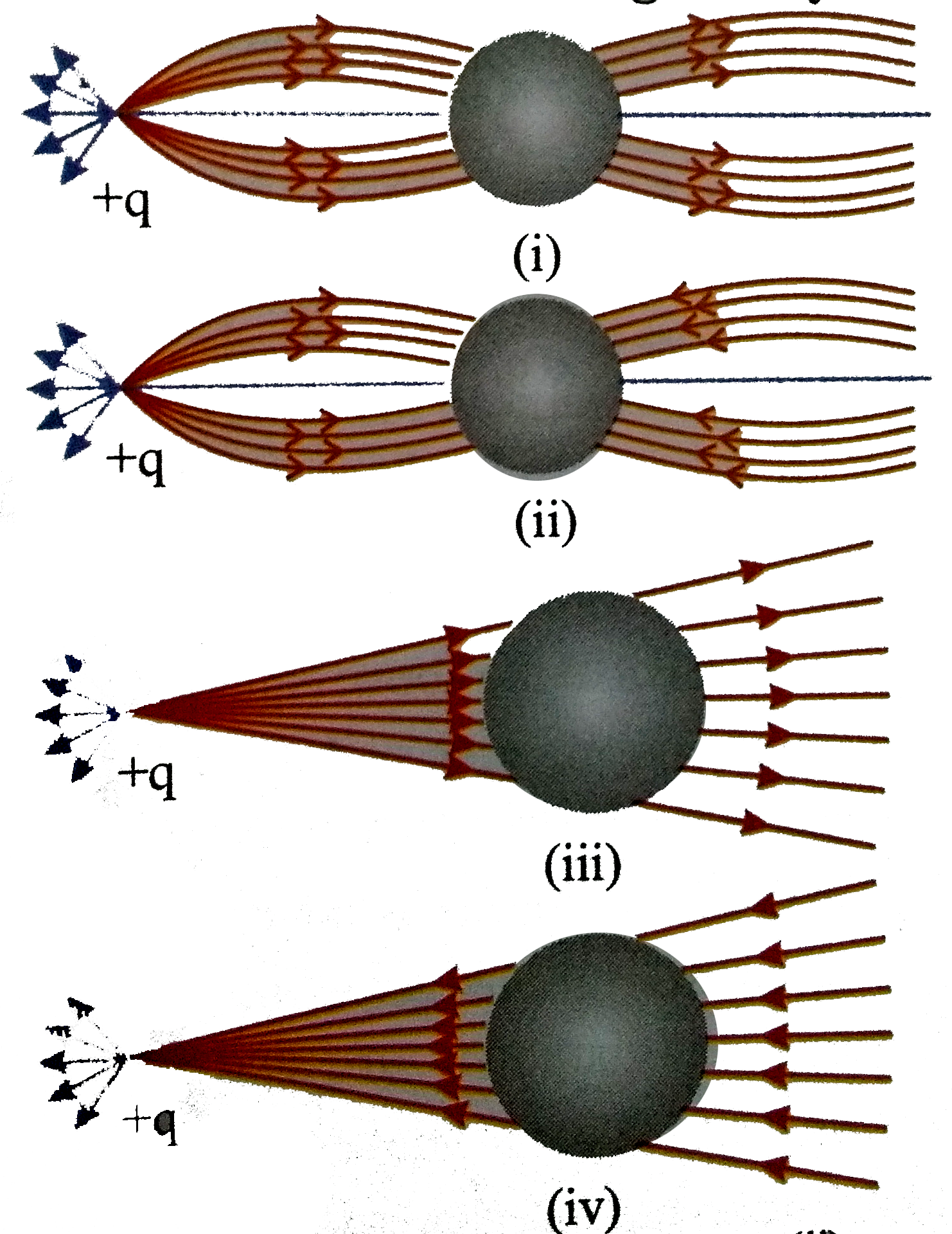
View SolutionA point positive charge is brought near an isolated conducting sphere as shown in figure the electric field is best given by
View SolutionThe electric flux through the surface

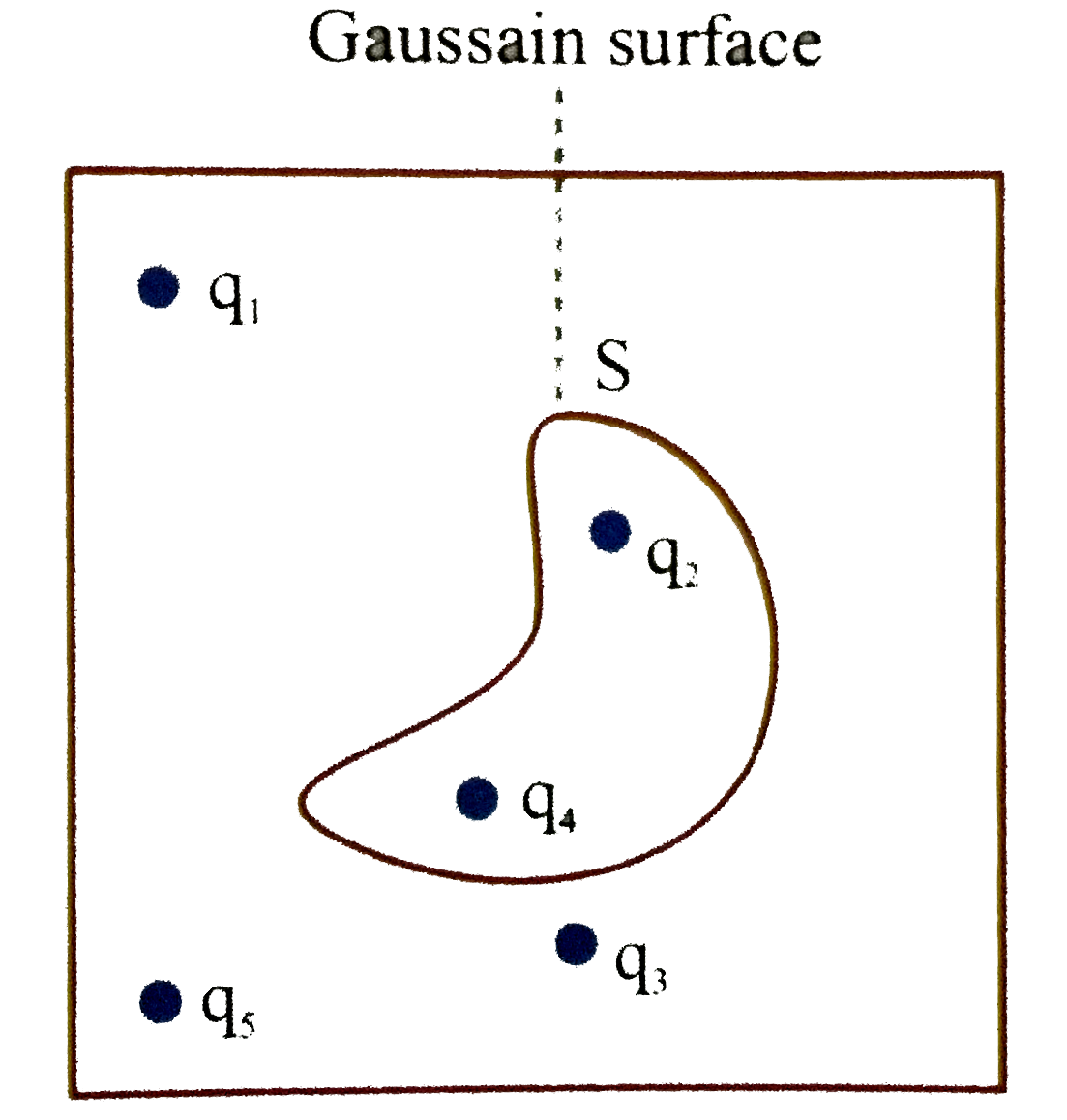
View Solutionfive charge `q_(1),q_(2),q_(3),q_(4)`and `q_(5)` are fixed at their positions as shown in figure .`s` is Gaussian surface .The Gauss's law is given by `ointvec(E).vec(ds)=(q)/(epsilon_(0))`
Which of the following statement is correct?
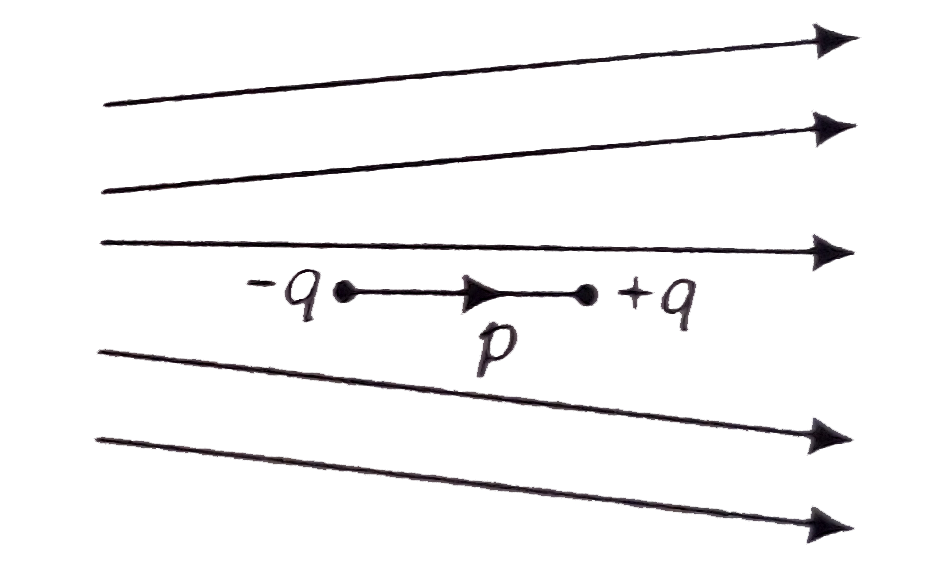
View SolutionFigure shows electric field lines in which an electric dipole p is placed as shown. Which of the following statements is correct ?
View SolutionA point charge `+q` is placed at a distance `d` from an isolated conducting plane. The field at a point `P` on the other side of plane is
View SolutionA hemispherical shell is uniformly charge positively. The electric field at point on a diameter away from the center is directed
View SolutionIf `oint_(s) E.ds = 0` Over a surface, then
View SolutionThe Electric field at a point is
View SolutionIf there were only one type of charge of the universe then
View SolutionConsider a region inside which there are various types of charges but the total charge is zero ,.At points outside the region
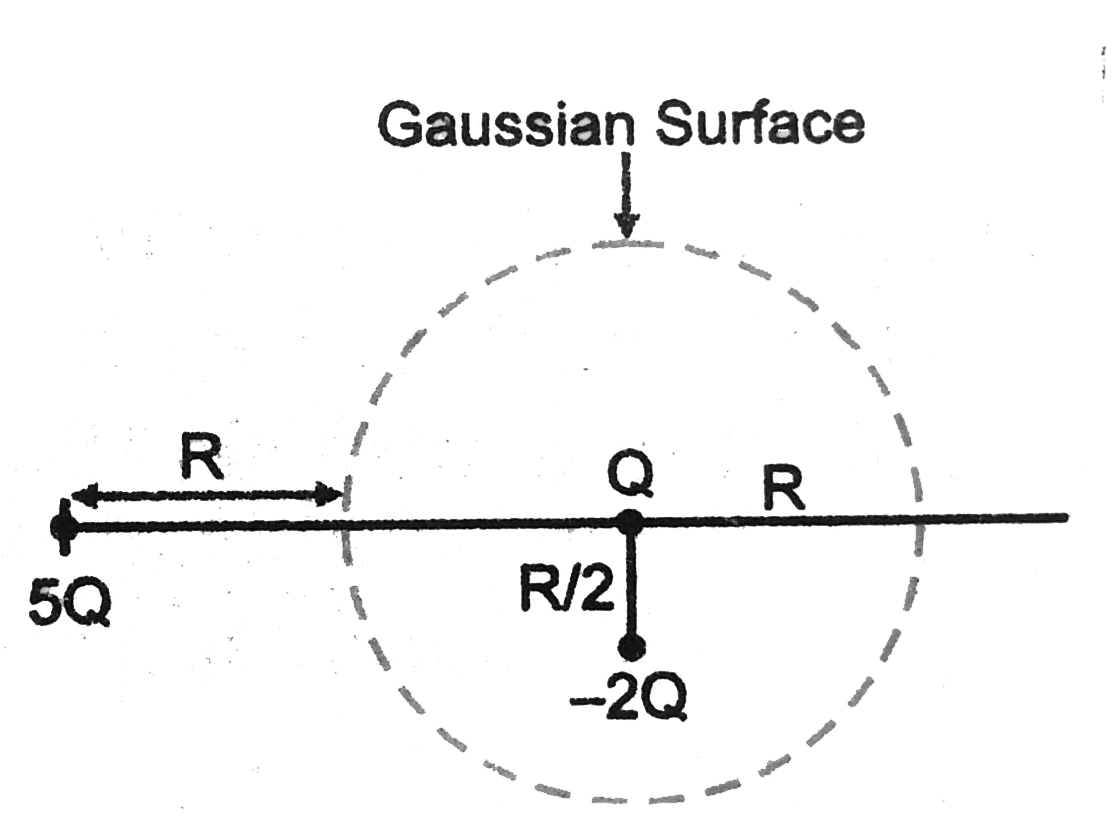
View SolutionRefer to the arrangement of charges in Fig and a Gaussian surface of radius `R` with `Q` at the centre. Then
View SolutionA positive charge `Q` is uniformly distributed along a circular ring of radius `R`. A small test charge `q` is placed at the centre of the ring.

View SolutionAn arbitrary surface encloses a dipole. What is the electric flux through this surface ?
View SolutionA metal spherical shell has an inner radius `R_(1)` and outer radius `R_(2)`. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionThe dimensions of an atom are of the order of an Angstrom. Thus there must be large electric fields between the protons and electrons. then Why the electrostatic field inside a conductor zero?
View SolutionIf the total charge enclosed by a surface is zero, does it imply that the electric field everywhere on the surface is zero ? Conversely, if the electric field everywhere on a surface is zero, does it imply that net charge inside is zero.
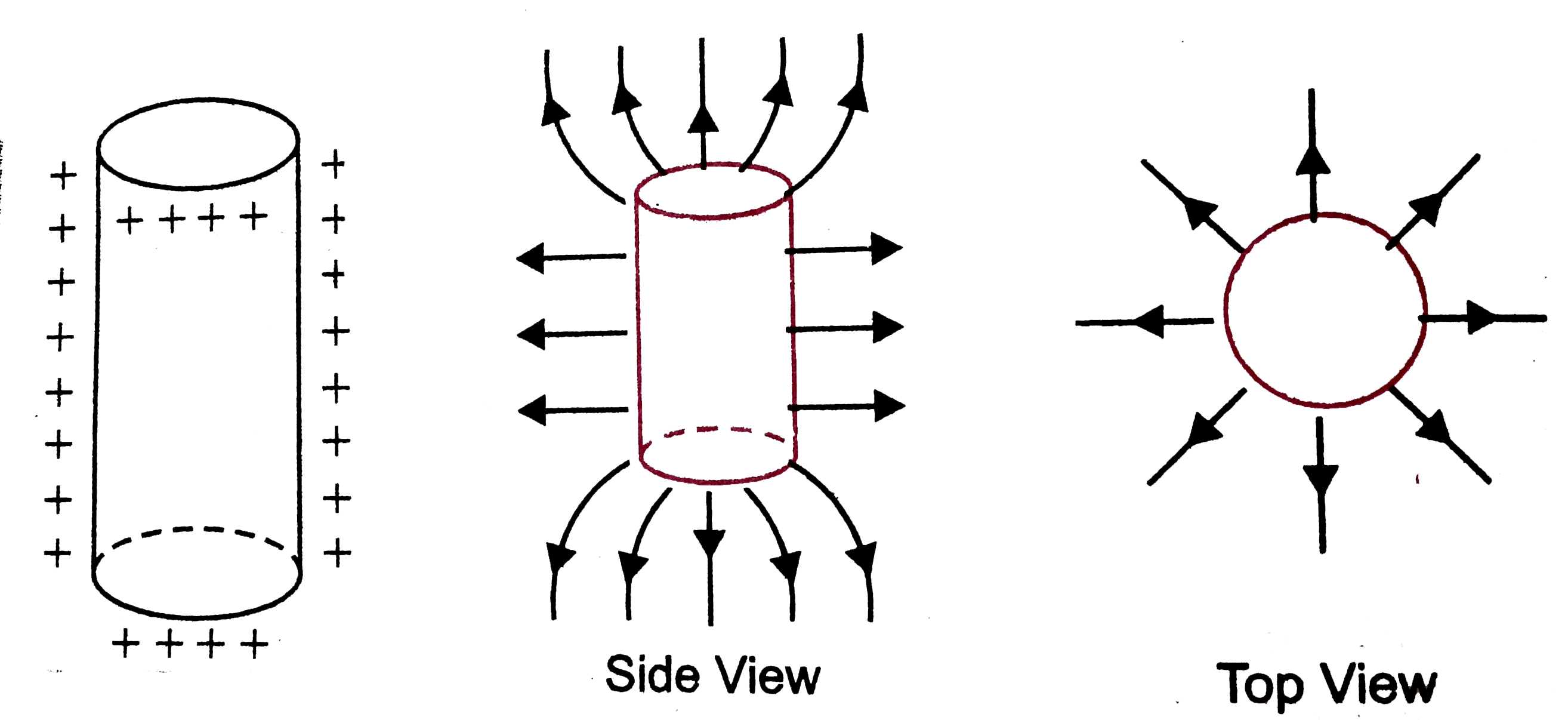
View SolutionSketch the electric field lines for a unifomly charged hollow cylinder shown in Fig.
View SolutionWhat will be the total flux through the faces of the cube, with side of length a if a charge q is placed at (a) A : a corner of the cube (b) B : mid-point of an edge of the cube (c) C : center of a face of the cube (d) D : mid-point of B and C.
View SolutionA paisa coin is made up Al-Mg alloy and weighs 0.75 g. It has a square shape and its diagonal measures 17mm. It is electrically neutral and constants equal amounts of positive and negative charges . Treating the paisa coin made up of only Al, find the magnitude of equal number of positive and negative charges. What conclusion do you draw from this magnitude ?
View SolutionConsider a coin, It is electrically neutral and contains equal amounts of positive and negative charge of magnitude 34.8 kC. Suppose that these equal charges were concentrated in two point charges separated by
(i) 1cm `(~(1)/(2)xx`diagonal of the one paisa coin`)`
(ii) 100 m (~length of a long building)
(iii) `10^(6)m` (radius of the earth). find the force on each such point charge in each of the three cases. what do you conclude from these results?
View SolutionFigure represents a crystal unit of cesium chloride, CsCl. The cesium atoms, represented by open circles are situated at the corners of a cube of side 0.40 mm, whereas a Cl atom is situated at the centre of the cube. The Cs atoms are deficient in one electron while the Cl atom carries an excess electron. ltBrgt (i). What is the net electric field on the Cl atom due to eight Cs atoms?
(ii) Suppose that the Cs atom at the corner A is missing. what is the net force now on the Cl atom due to seven remaining Cs atom?

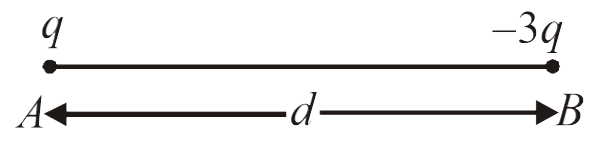
View SolutionTwo charge q and `–3q` are placed fixed on x–axis separated by distance d. Where should a third charge` 2q` be placed such that it will not experience any force ?
View SolutionFig. shows the electric field lines around three points charges A,B,C.
(a) Which charges are positive ?
(b) Which charge has the largest magnitude ? Why ?
(c) In which regions of the picture could be the electric field be zero? Justify your answer.
(i) near A, (ii) near B, (iii) near C, (iv) nowhere.
View SolutionFive charges , q each are placed at the corners of a regular pentagon of side.

(a) (i) What will be the electric field at 0, the centre of the pentagon?
(ii) What will be the electric field at 0 if the charge from one of the corners (say A) is removed?
(iii). What will be the electric field at 0 if the pentagon is replaced by n-sided regular polygon with charge q at each of its corner?
View SolutionIn 1959 Lyttleton and Bondi suggested that the expansion of the universe could be explained if matter carried a ent charge. Suppose that the universe is made up of hydrogen atoms with a number density N, which is maintained a constant. Let the charge on the proton be `e_(p)=-(1+y)e` where e is the electronic charge.
(a). find the critical value of y such that expansion may start. ltBrgt (b) show that the velocity of expansion is proportional tot he distance from the centre.
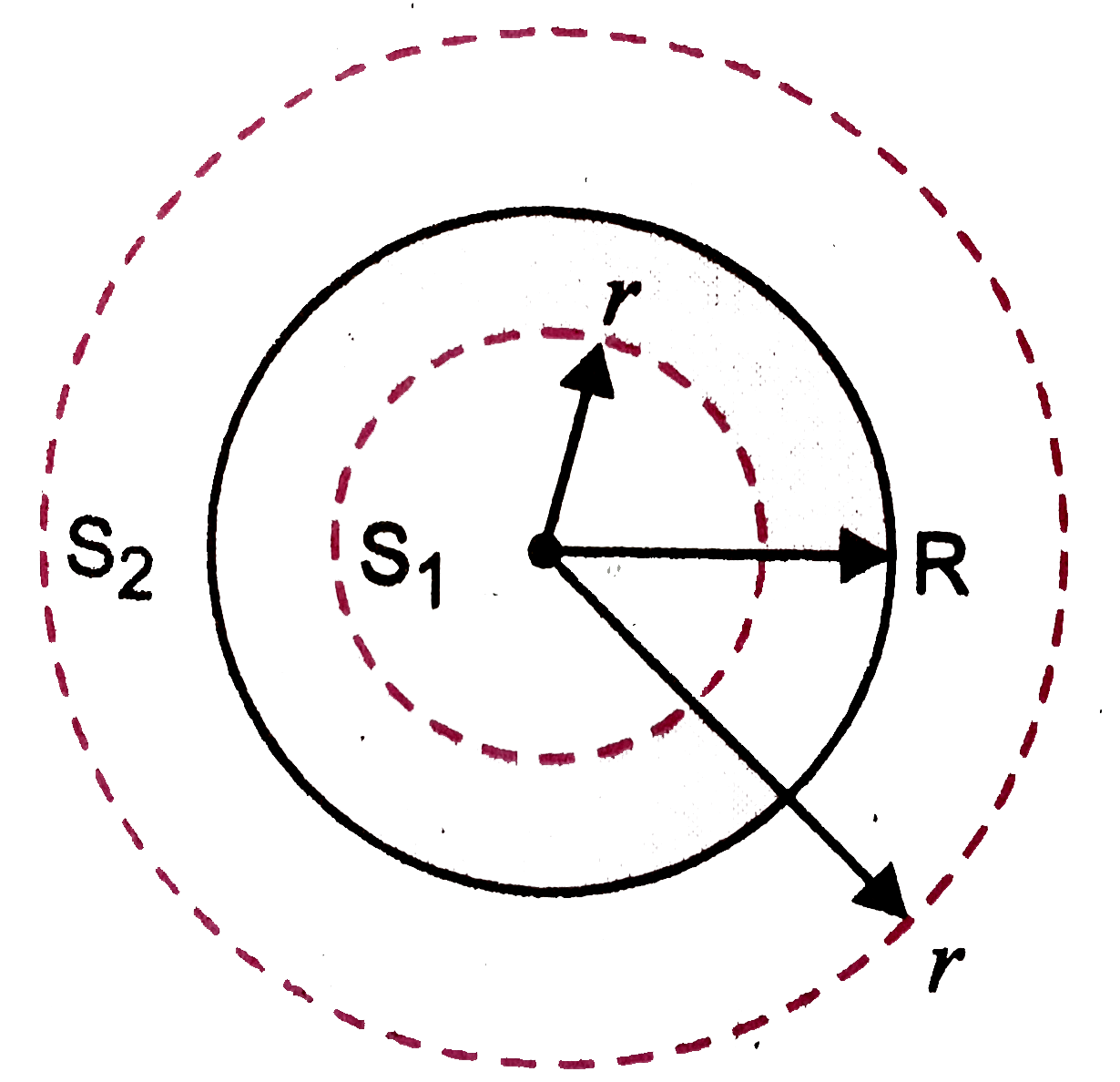
View SolutionConsider a sphere of radius R with charge density distributed as `rho (R) = kr` for `r le R, rho (R) = 0` for `r gt R`.
(a) Find the electric field at all points r.
(b) suppose the total charge on the sphere is 2e, where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.
View SolutionTwo fixed, identical conducting plates `(alpha and beta)`, each of surface area S are charged to -Q and q, respectively, where Q `gt` q `gt` 0. A third identical plate `(gamma)`, free to move is located on the other side of the plate with charge Q at a distance d (figure). The third plate is released and collides with the plate `beta`. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst `beta and gamma`.
(a) Find the electric field acting on the plate `gamma` before collision.
(b) Find the charges on `beta and gamma` after the collision.
(c) Find the velocity of the plate `gamma` after the collision and at a distance d from the plate `beta.`
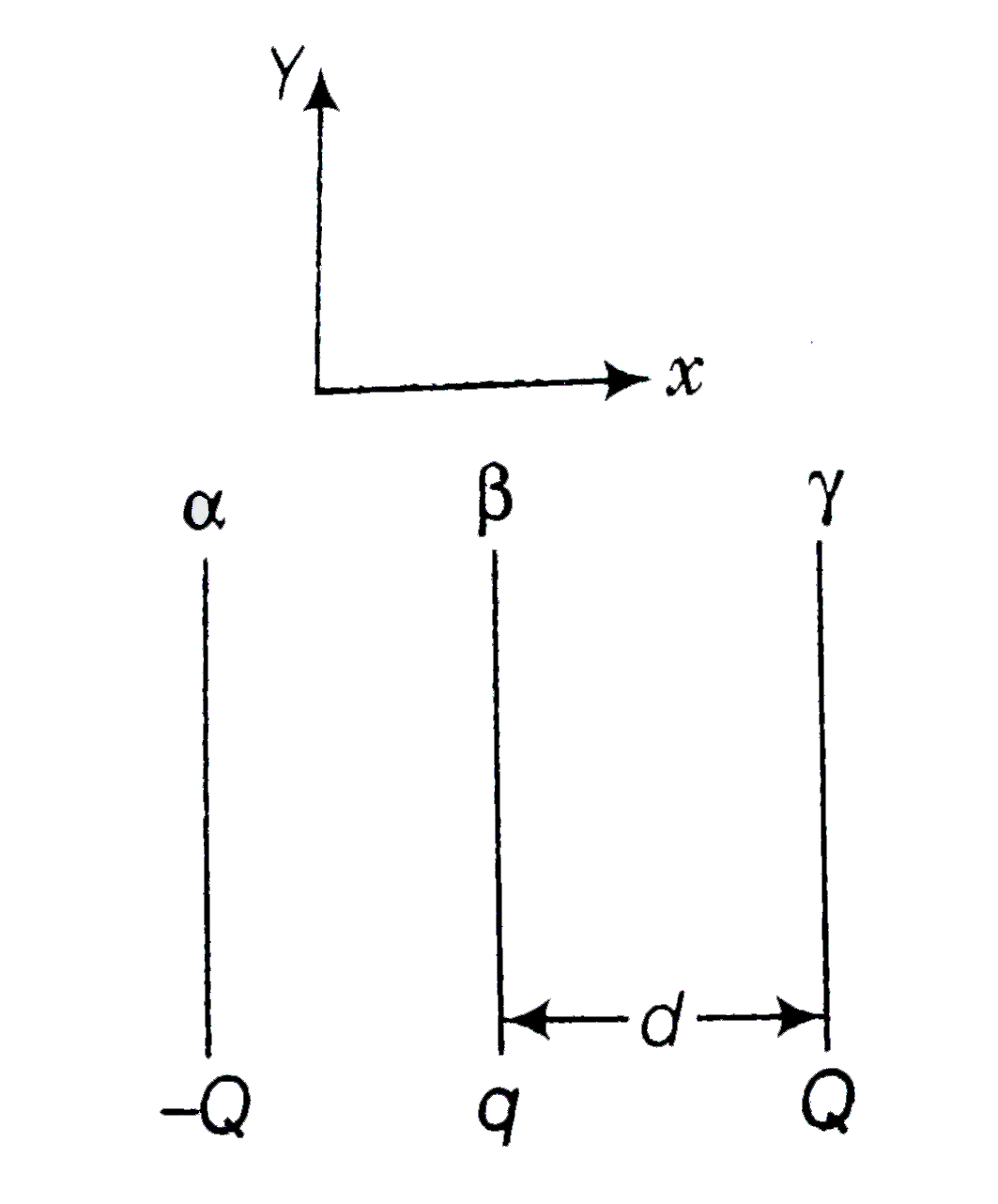
View SolutionThere is another useful system of units, besides the SI/MKS. A system, called the CGS (centimeter-gram-second) system. In this system, coulomb's law is given by `F=(Qq)/(r^(2))hatr`
where the distance r is measured in `cm(=10^(-2)mu)`, F in dynes `(=10^(-5)N)` and the charges in electrostatic units (es units), where 1 es unit of charge `=(1)/([3])xx10^(-9)C`. The number [3] actually arises from the speed of light in vaccum which is now taken to be exactly given by `c=2.99792458xx10^(8)m//s`. An approximate value of c, then is `c=3xx10^(8)m//s`.
(i). Show that the coulomb's law in CGS units yields 1 esu of charge `=1("dyne")^(1//2)`cm. Obtain the dimensions of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of cahrge `=xC`, where x is a dimensionless number. Show that this gives `(1)/(4epsi_(0))=(10^(-9))/(x^(2))(Nm^(2))/(C^(2))`. With `x=(1)/([3])xx10^(-9)`, we have
`(1)/(4piepsi_(0))=[3]^(2)xx10^(9)(Nm^(2))/(C^(2)),(1)/(4piepsi_(0))=(2.99792458)^(2)xx10^(9)(Nm^(2))/(C^(2))` (exactly)
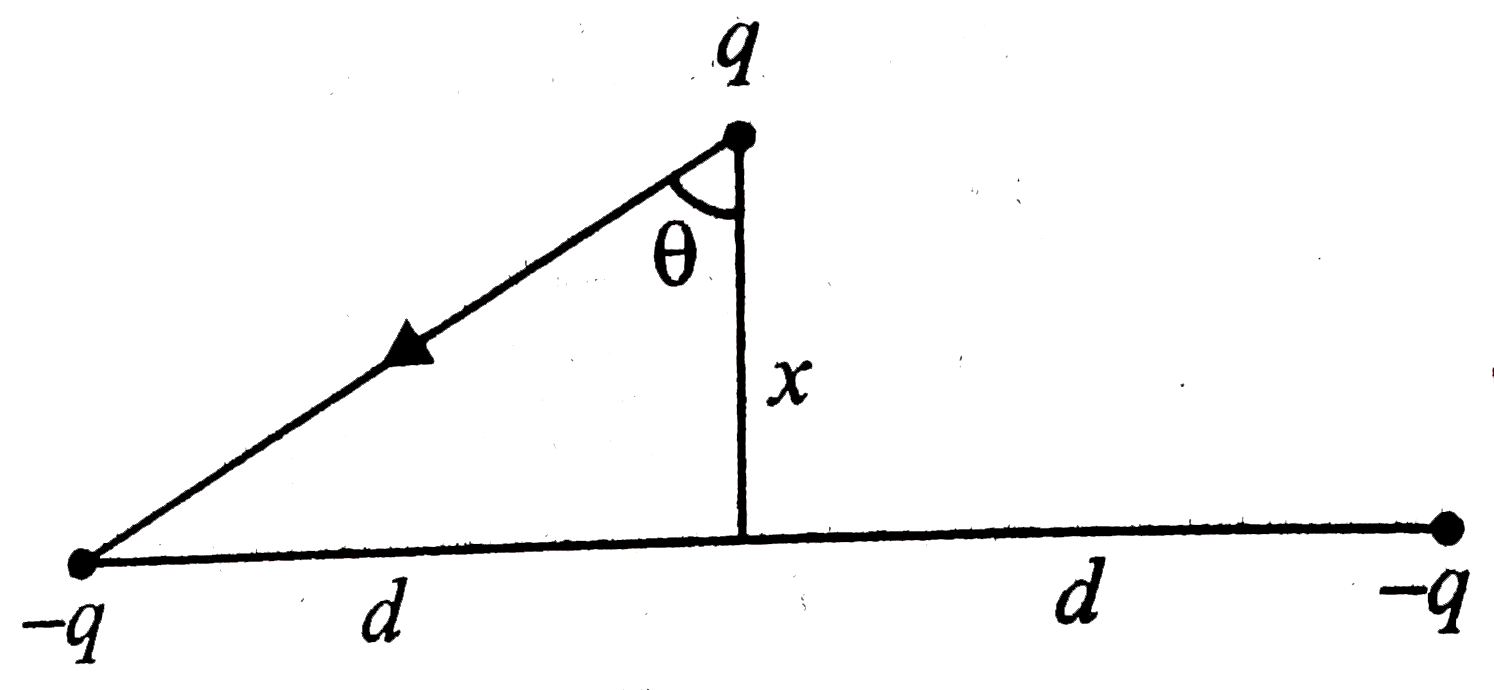
View SolutionTwo charges `-q` each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced at the mid-point is placed slightly by `x (xltltd)` perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillation of time period.
`T = [(8pi^(3) in_(0) md^(3))/(q^(2))]^(1//2)`
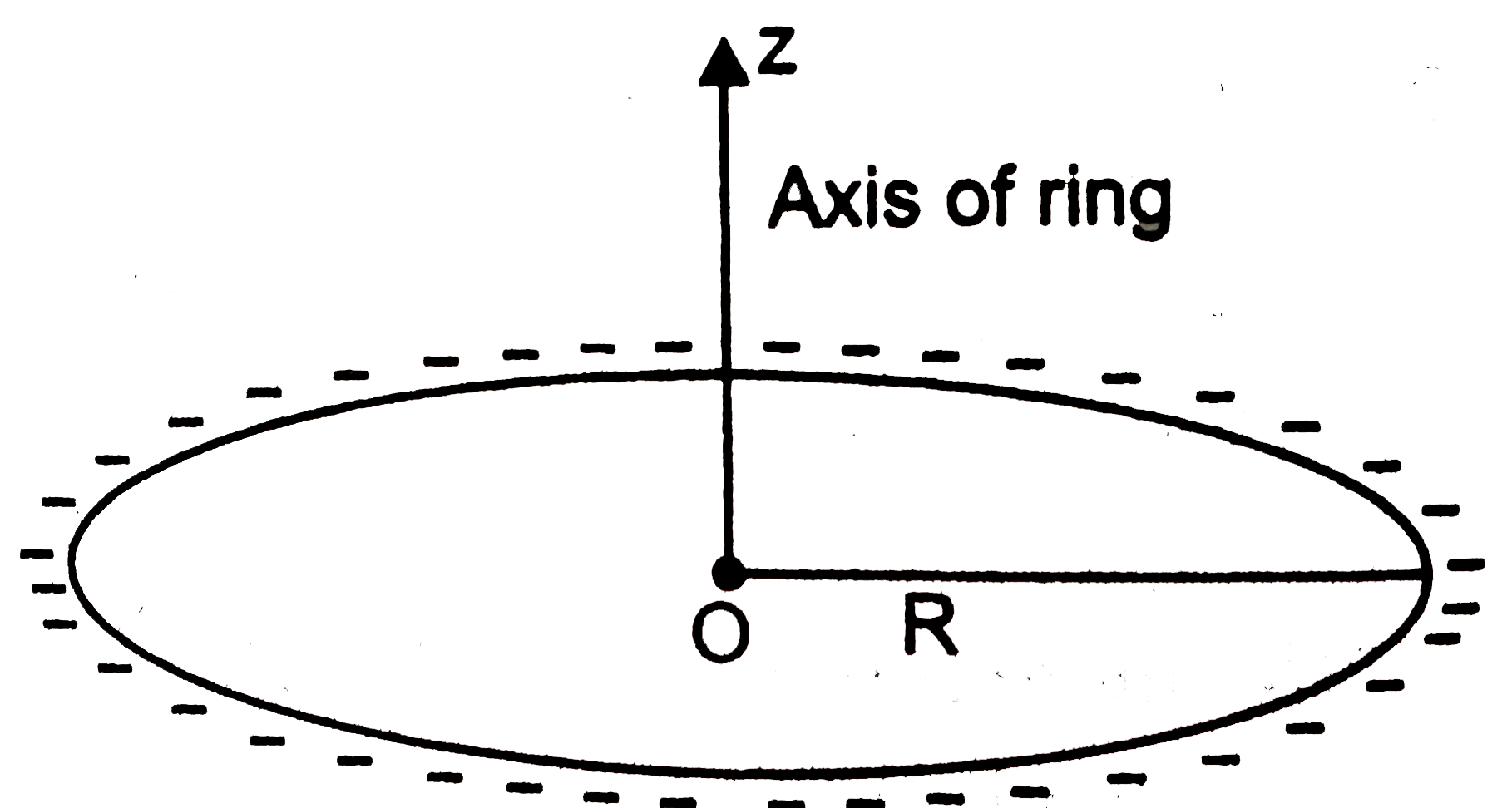
View SolutionTotal charge `-Q` is uniformly spread along length of a ring of radius R. A small test `+q` of mass m is kept at the center of the ring .
(a) Show that the particle executes a single harmonic oscillation.
(b) Obtain its time period.
View Solution
Electric Charges And Field questions and complete solutions for chapter ELECTRIC CHARGES AND FIELD of NCERT PHYSICS (HINGLISH) of Class 12