Two fixed, identical conducting plates (αandβ), each of surface area S are charged to -Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge Q at a distance d (figure). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst βandγ.
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on βandγ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
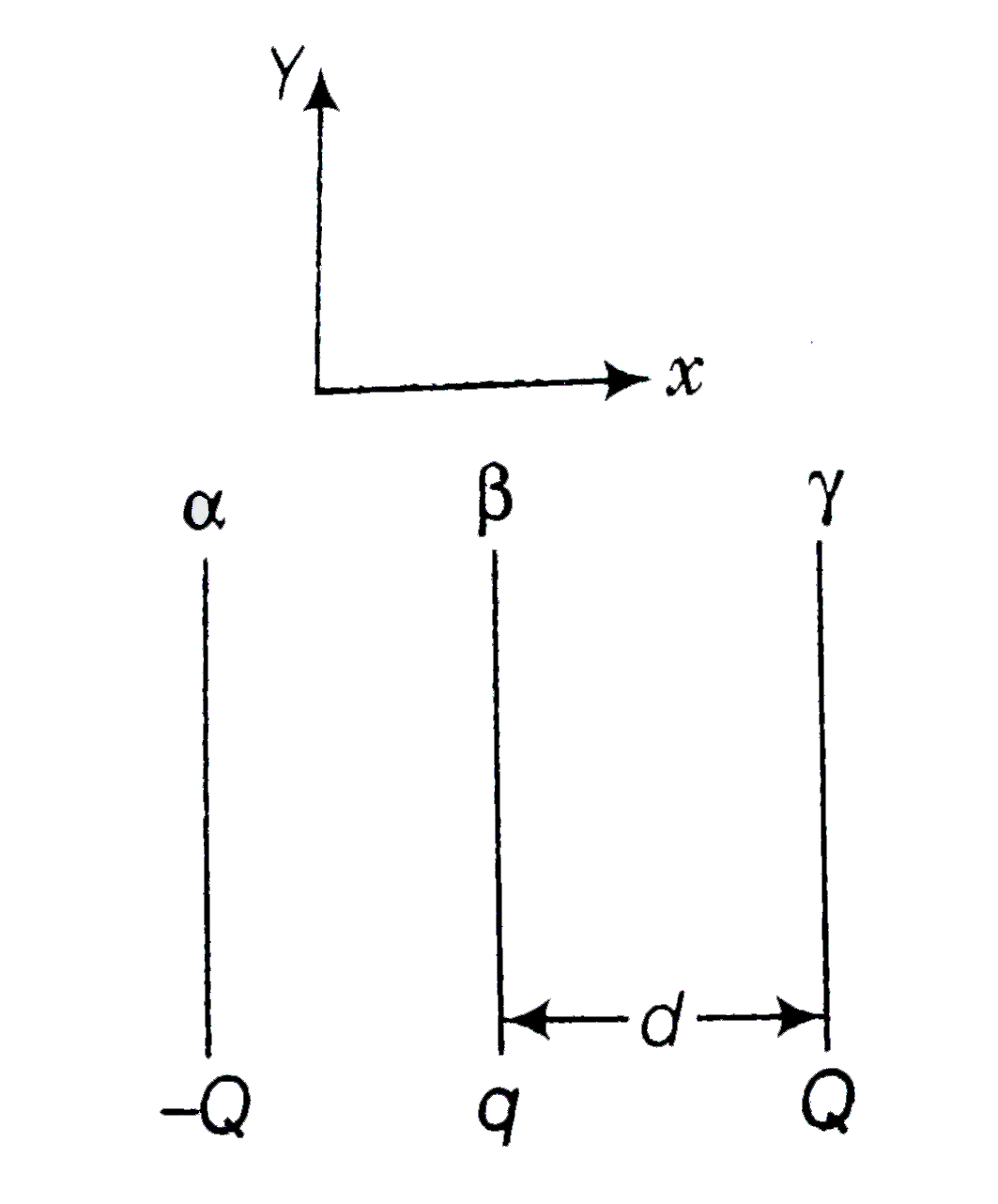
(a). Find electric field at plate γ before collision is equal to the sum of electric field at plate γ due to plate αandβ.
The electric field at plate γ due to plate α is E1=−QS(2ε0) to the left.
The electric field at plate γ due to plate β is E2=qS(2ε0), to the right
Hence, the ent electric field at plate γ before collision,
E=E1+E2=q−QS(2ε0), to the left if Q>q
(b) During collision, plates βandγ are together. Their potentials become same.
Suppose charge on plate β is q1 and cahrge on plate γ is q2. At any point O, in between the two plates, the electric field must be zero.
Electric field at O due to plate α=−QS(2ε0), to the left
Electric field at O due to plate β=q1S(2ε0), to the right ltBrgt Electric field at O due to plate γ=q2S(2ε0), to the left
As the electric field at O is zero, therefore ltBrgt Q+q2S(2ε0)=q1S(2ε0)
∴Q+q2=q1
Q=q1+q2 . . .(i)
As there is no loss of charge o collision, ltBrgt Q+q=q1+q2
On solving eqs. (i) and (ii), we get
q1=(Q+q/2)=charge on plate β
q2=(q/2)=charge on plate γ
(c) After collision, at a distance d from plate β.
Let the velocity of plate γ be v. After the collision, electric field at plate γ is
E2=−Q2ε0S+(Q+q/2)2ε0S=q/22ε0S to the right
just before collision, electric field at plate γ is E1=Q−q2ε0S
If F1 is force on plate γ before collision, then F1=E1Q=(Q−q)Q2ε0S
Total work done by the electric field is round trip movement of plate γ
W=(F1+F2)d
=[(Q−q)Q+(q/2)2]d2ε0S=(Q−q/2)2d2ε0S ltBrgt If m is mass of plate γ, the KE gained by plate γ=12mv2
According to work-energy principle, 12mv2=W=(Q−q/2)2d2ε0S
γ=(Q−q/2)(dmε0S)1/2.
Topper's Solved these Questions
Similar Questions
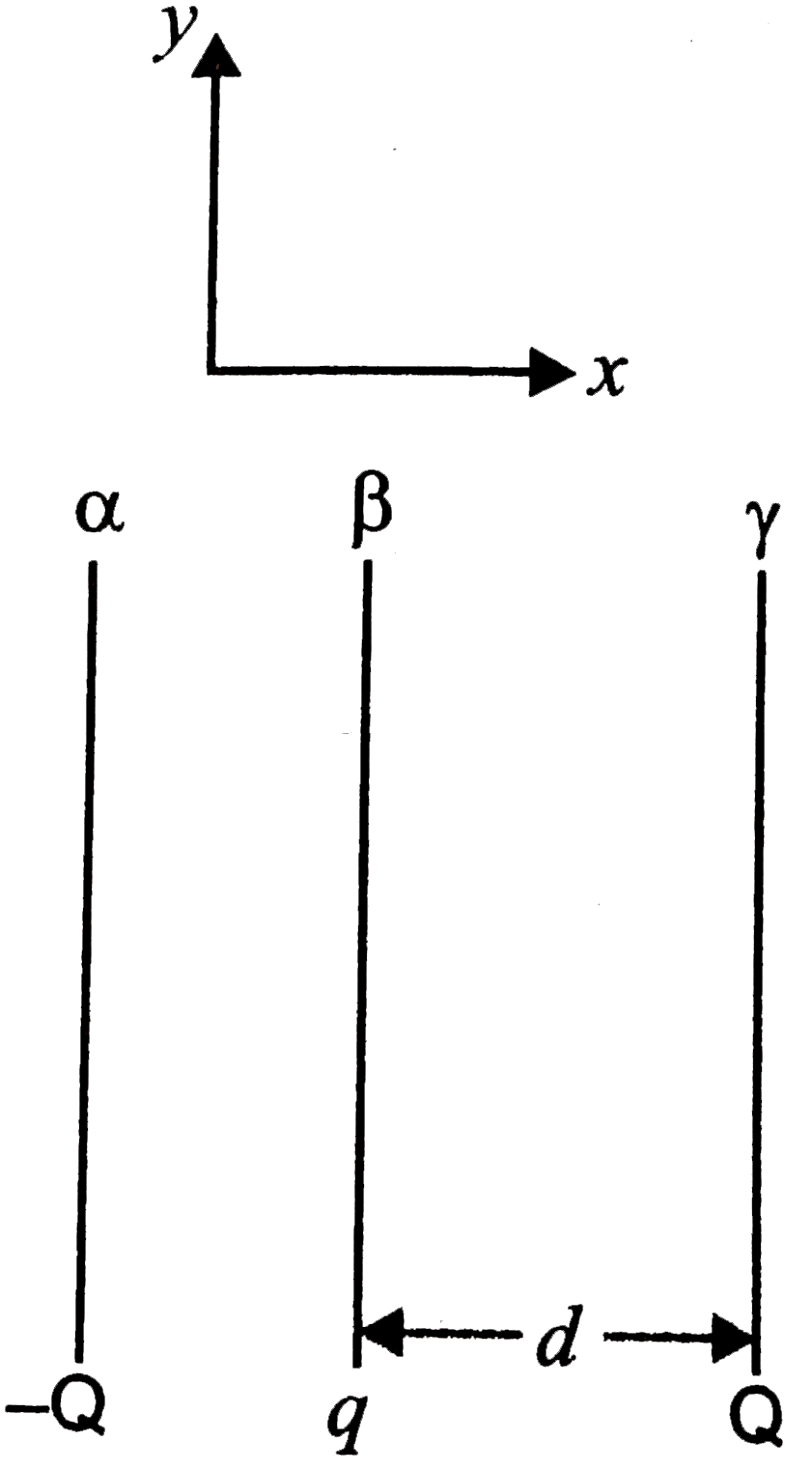
Two fixed, identical conducting plates (αandβ), each of surface area S are charged to −Qandq, respectively, where Q>q>0. A third indentical plate (γ), free to move is located on the other side of the plate with charge q at a distance d, fig. The third plate is released and collidies with the plate β. Assume the collsion is electric and the time of collision is sufficient to redistribute charge amongst βandγ.
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charge on βandγ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
View SolutionForce between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
View Solution
Knowledge Check
Three identical conducting plates P1,P2 and P3 are kept at a distance d from each other. If q,-q,2q are the charges in P1,P2 and P3 respectively, the electric field between P1 and P2 is (where A is area of plate)
A(q2Aε0)B(2q2Aε0)C0D(4q2Aε0)
Force between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
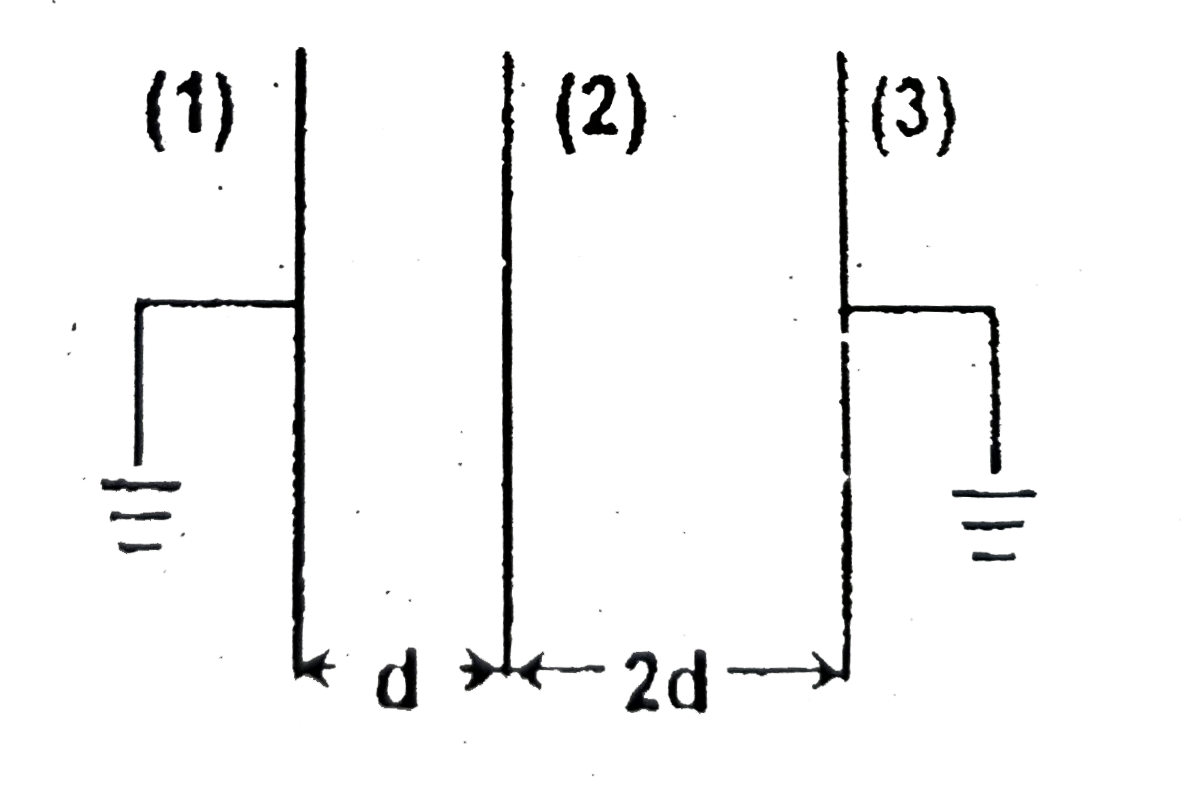
View SolutionThree identical plates of area A are arranged as shown. A charge +Q is given to plate (2). Then,
View SolutionTwo identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.
View SolutionTwo identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionThree identical metallic plates are kept parallel to one another at separations a & b as shown in figure. The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate. Find the charge on all the six sufaces.
View Solution
