Complete Solutions to Electromagnetic Induction of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| NCERT EXEMPLAR | Electromagnetic Induction |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
A square of side L meters lies in the x-y plane in a region, where the magnetic field is given by `B = B_(0) (2 hati + 3 hat j + 4 hatk)`T, where `B_(0)` is constant. The magnitude of flux passing through the square is
View SolutionA loop made of straight edges has six corners at `A(0,0,0), B(L, O,0), C(L,L,0), D(0,L,0), E(0,L,L)` and `F(0,0,L)`. Where `L` is in meter. A magnetic field `B = B_(0)(hat(i) + hat(k))T` is present in the region. The flux passing through the loop `ABCDEFA` (in that order) is
View SolutionA cylindrical bar magnet is rotated about its axis (Figure). A wire is connect from the axis and is made to touch the cylindrical surface through a contact. Then
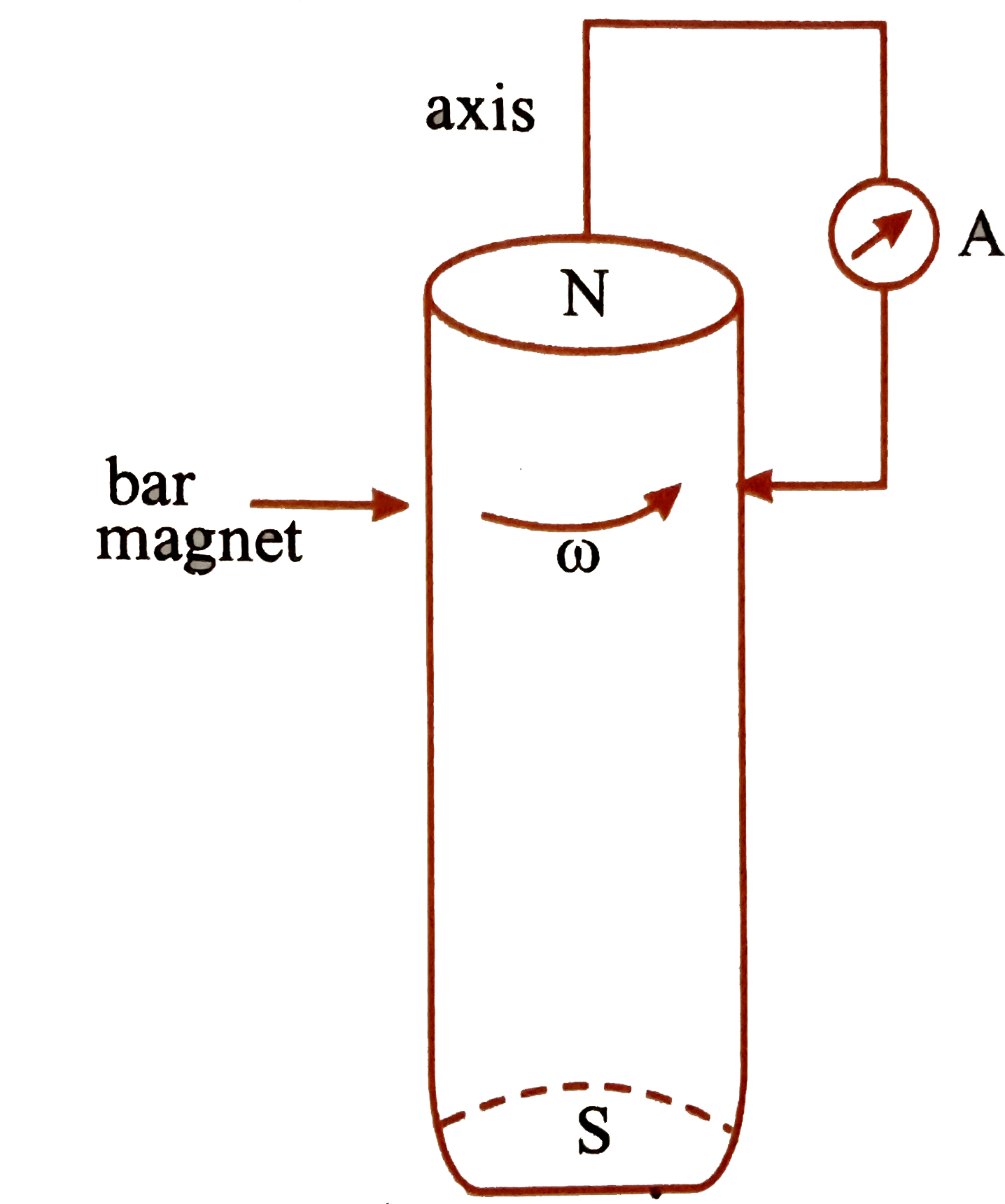
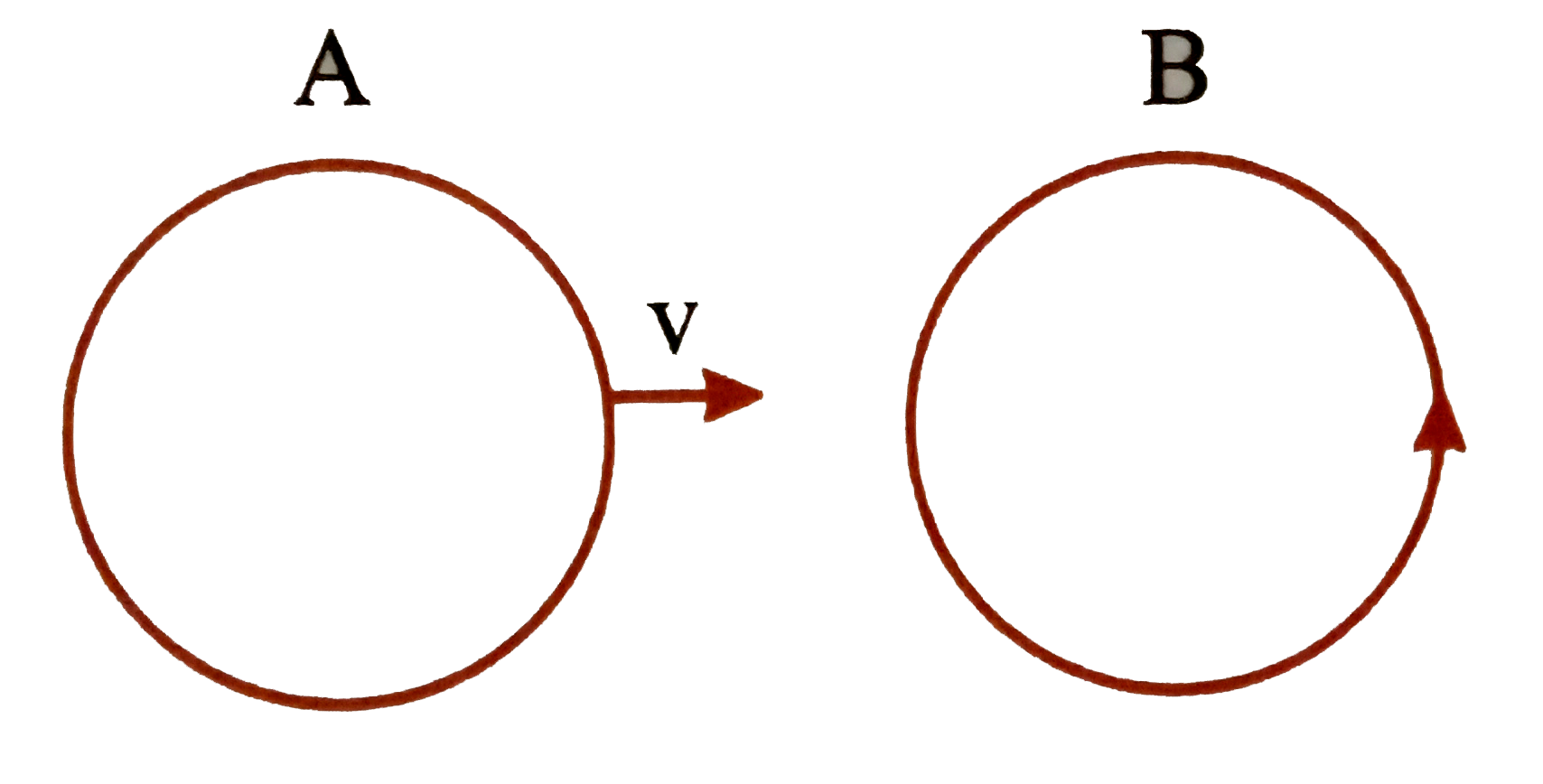
View SolutionThere are two coils `A` and `B` as shown in Figure. A current starts flowing in `B` as shown, when `A` is moved towards `B` and stops when `A` stops moving. The current in `A` is counterclockwise. `B` is kept stationary when `A` moves. We can infer that
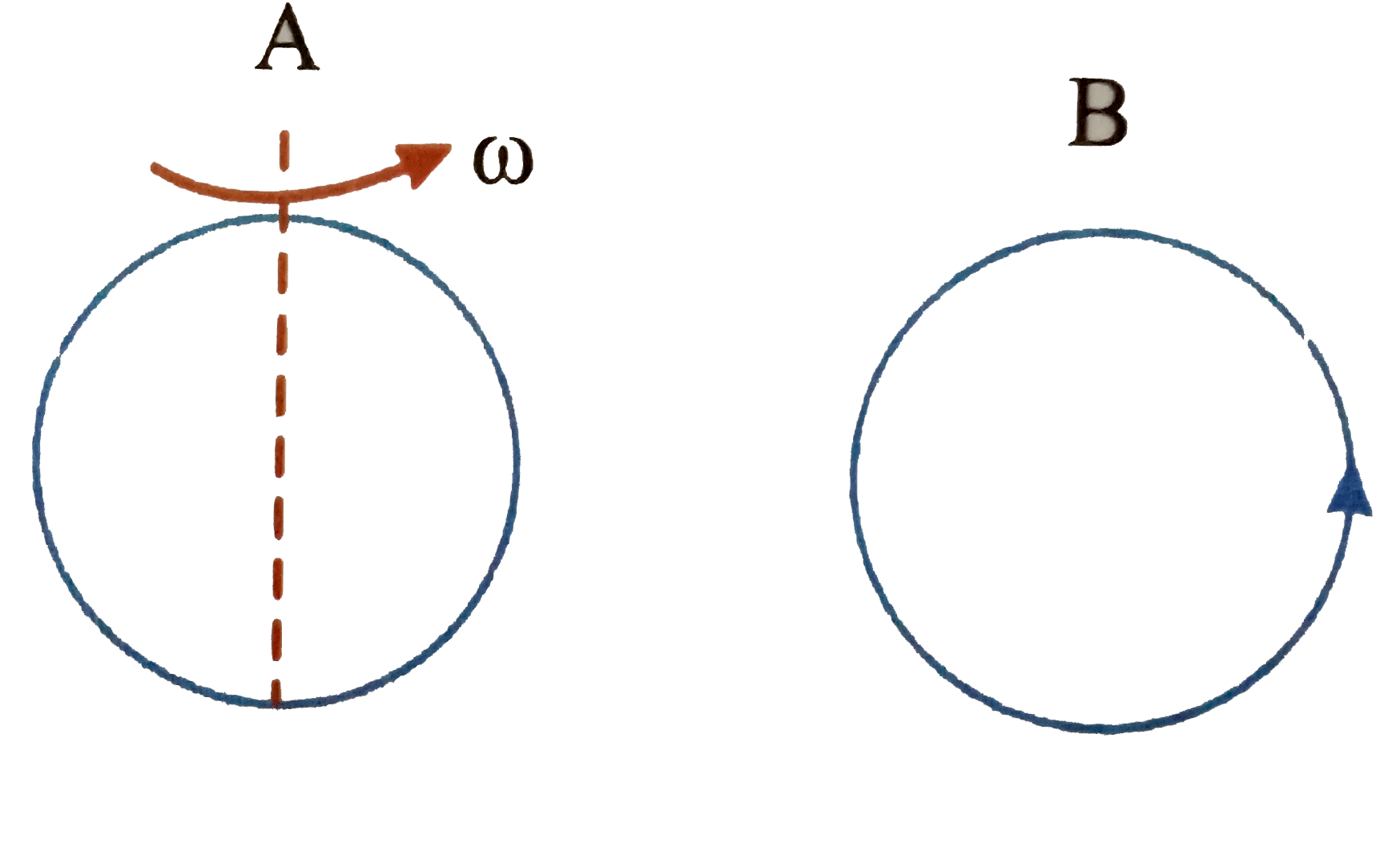
View SolutionSame as problem `4` except the coil `A` is made to rotate about a vertical axis in the plane of the coil (Figure). No currents flows in `B` if `A` is at rest. The current in coil `A`, when the current in `B` (at `t = 0`) is counterclockwise and the coil `A` is as shown at this instant, `t = 0`, is
View SolutionThe self inductance L of a solenoid of length `l` and area of cross-section A, with a fixed number of turns N increases as
View SolutionA metal plate is getting heated. It can be because
View SolutionAn e.m.f. is produced in a coil, which is not connected to an external voltage source. This can be due to
View SolutionThe mutual inductance `M_(12)` of coil 1 with respect to coil 2
View SolutionA circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because
View SolutionConsider a magnet surround by a wire with an on`//` of switch `S` (figure) if the switch is thrown from the off position (open circuit) to the on position the (closed circuit).
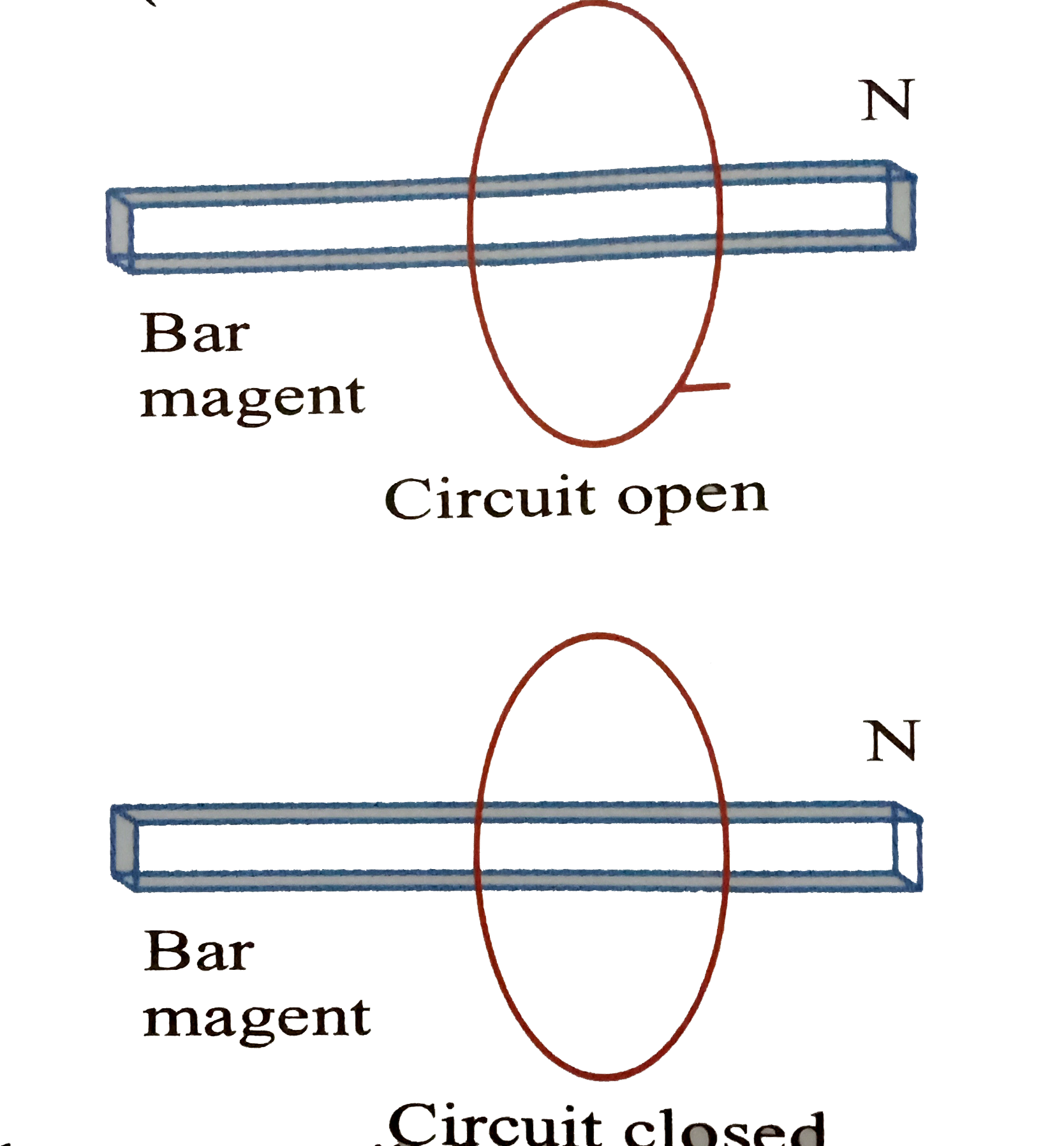
View SolutionA wire in the form of a tightly would solenoid is connected to a `DC` source, and carries a current. If the coil is stretched so that there are gaps between successive elements of the spiral coil, then
View SolutionA solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, then
View SolutionConsider a metal ring kept on top of a fixed solenoid (say on a carboard) The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on then
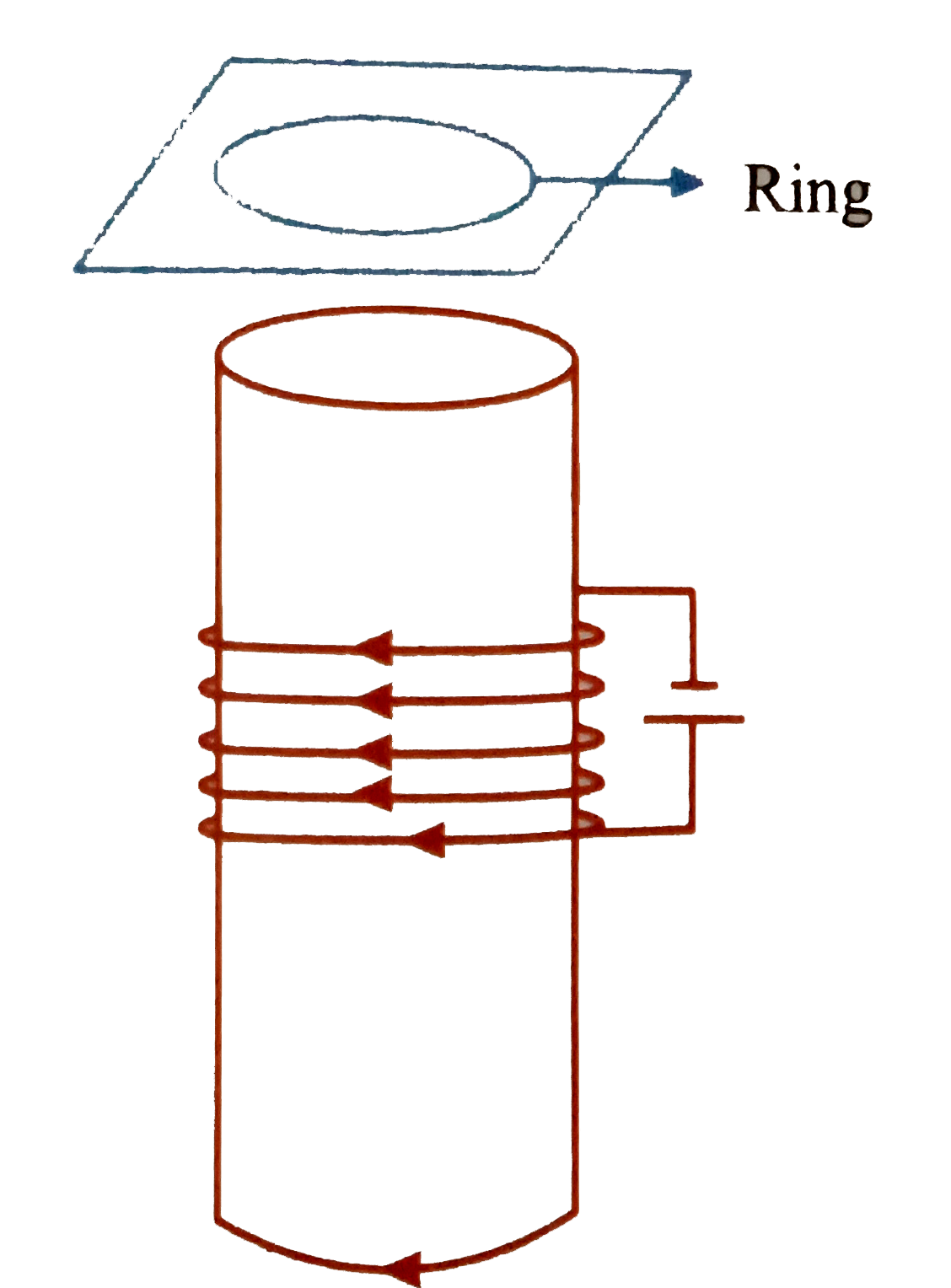
View SolutionConsider a metal ring kept on top of a fixed solenoid (say on a carboard) The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on then

View SolutionConsider a metallic pipe with an inner radius of 1 cm. If a cylindrical bar magnet of radius 0.8 cm is dropped through the pipe, it takes more time to come down than it takes for a similar unmagnetised cylindrical iron bar dropped through the metallic pipe. Explain.
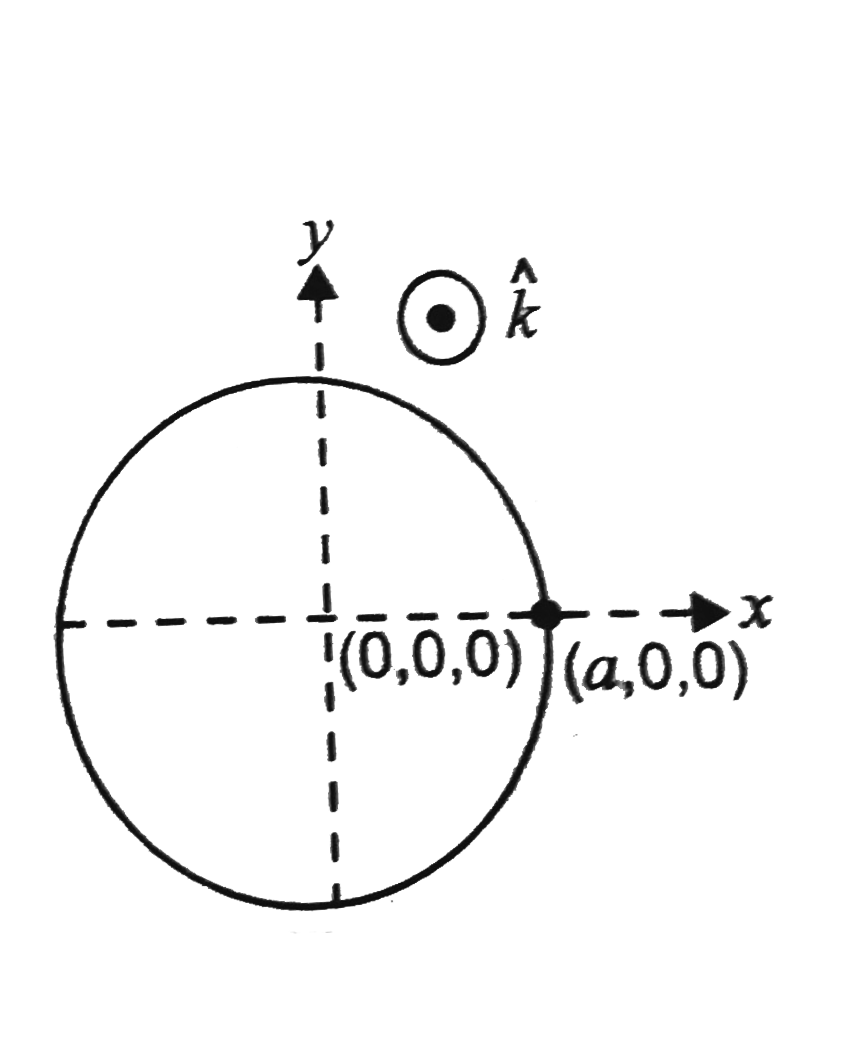
View SolutionA magnetic field in a certain region is given by `B = B_(0) cos (omega t) hat k` and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field, Fig. Find the magnitude and the direction of the current at (a,0,0) `at t = pi//2 omega, t = pi//omega` and `t = 3 pi//2 omega`.
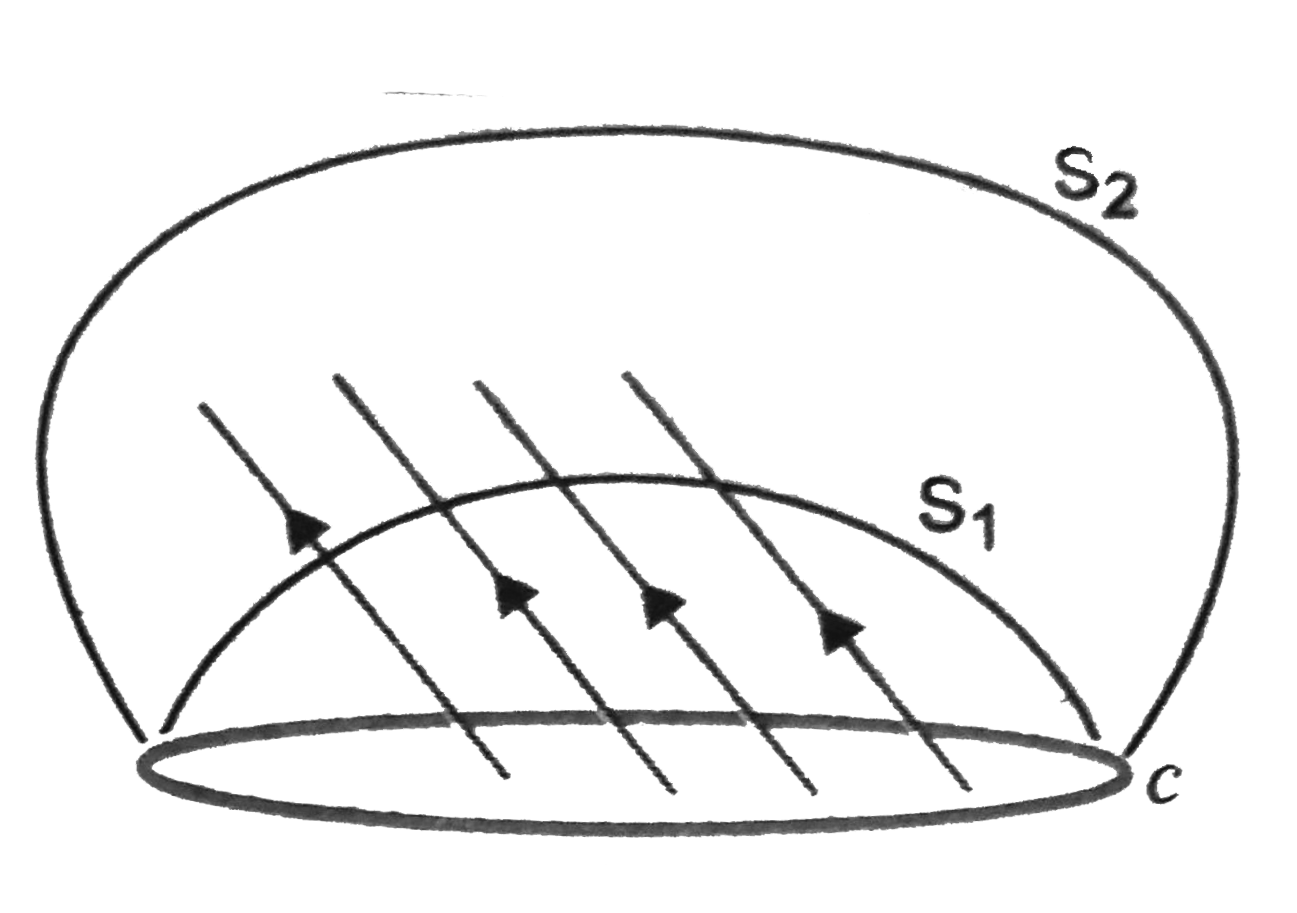
View SolutionConsider a closed loop C in a magnetic field, Fig. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula `phi = B_(1) .dA_(1) + B_(2). Da_(2) +`……..Now if we chose two different surfaces `S_(1)` and `S_(2)` having C as their edge, would we get the same answer for flux. Justify your answer.
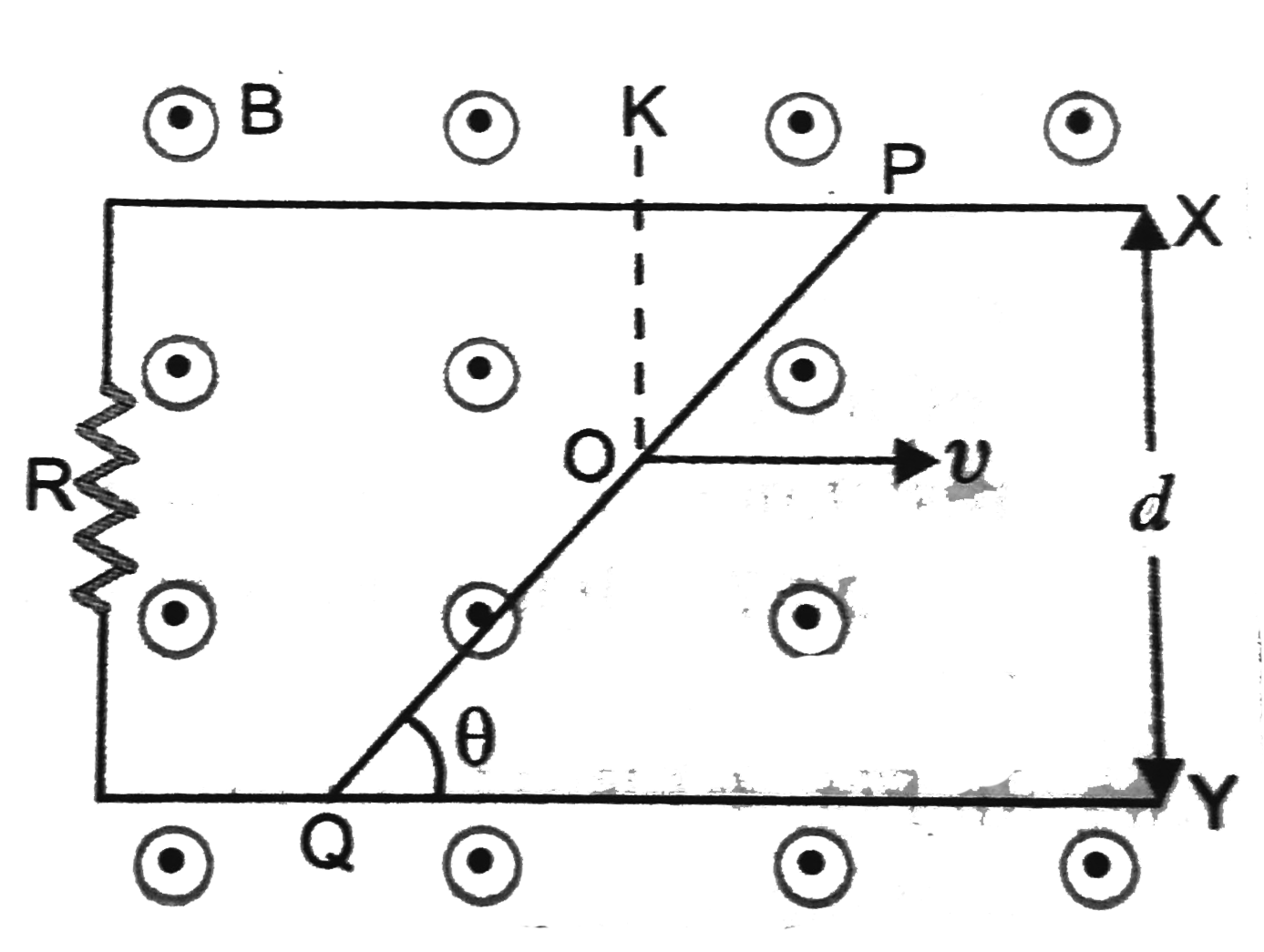
View SolutionFind the current in the wire PQ for the configuration shown in Fig. Wire PQ has negligible resistance. B, the magnetic field is coming out of the paper. `theta` is a fixed angle made by PQ travelling smoothly over two conducting parallel wires seperated by a distance d.
View SolutionA (current vs time) graph of the current passing through a solenoid is shown in Fig. For which time is the back electromotive force (u) a maximum? If the back emf t = 3 s is e, find the back emf at t = 7 s, 15 s and 40 s OA, AB and BC are straight line segments.
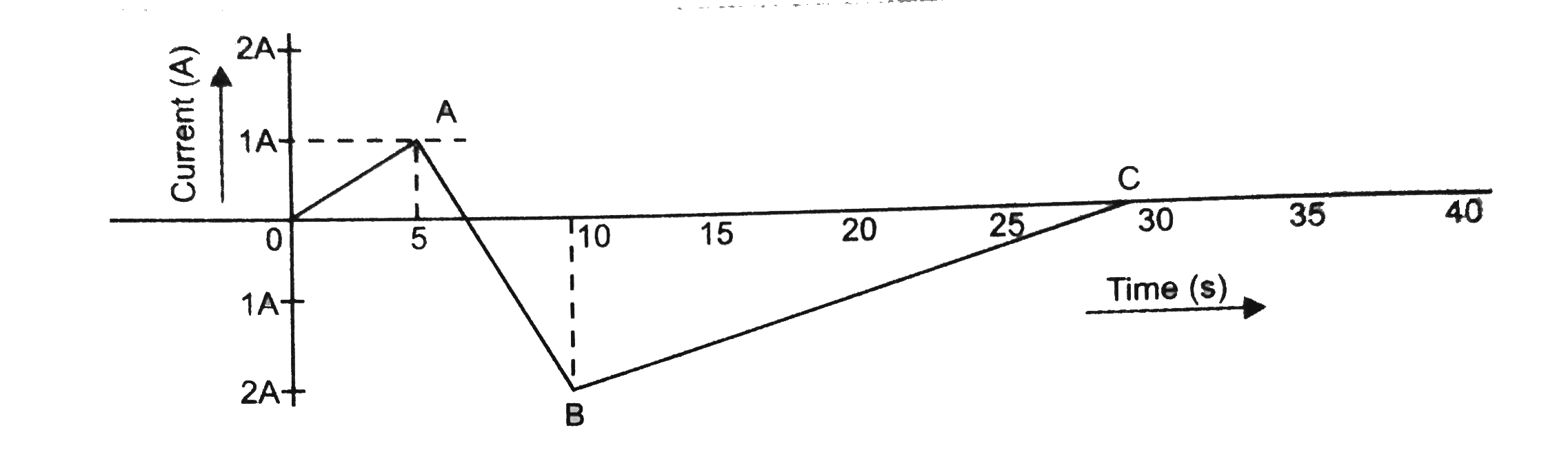
View SolutionThere are two coils A and B seperated by some distance. If a current of 2 A flows through A, a magnetic flux of `10^(-2)` Wb passes through B (no current through B). If no current passes through A and a current 1 A passes through B, what is the flux through A?
View SolutionA magnetic field `B = B_(0) sin (omega t) hat k` covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d, Fig. The wires are in the x-y plane. The wire AB (of length d) has resistance R and parallel wires have negligible resistance. If AB is moving with velocity `upsilon`, what is the current in the circuit ? What is the force needed to keep the wire moving at constant velocity ?
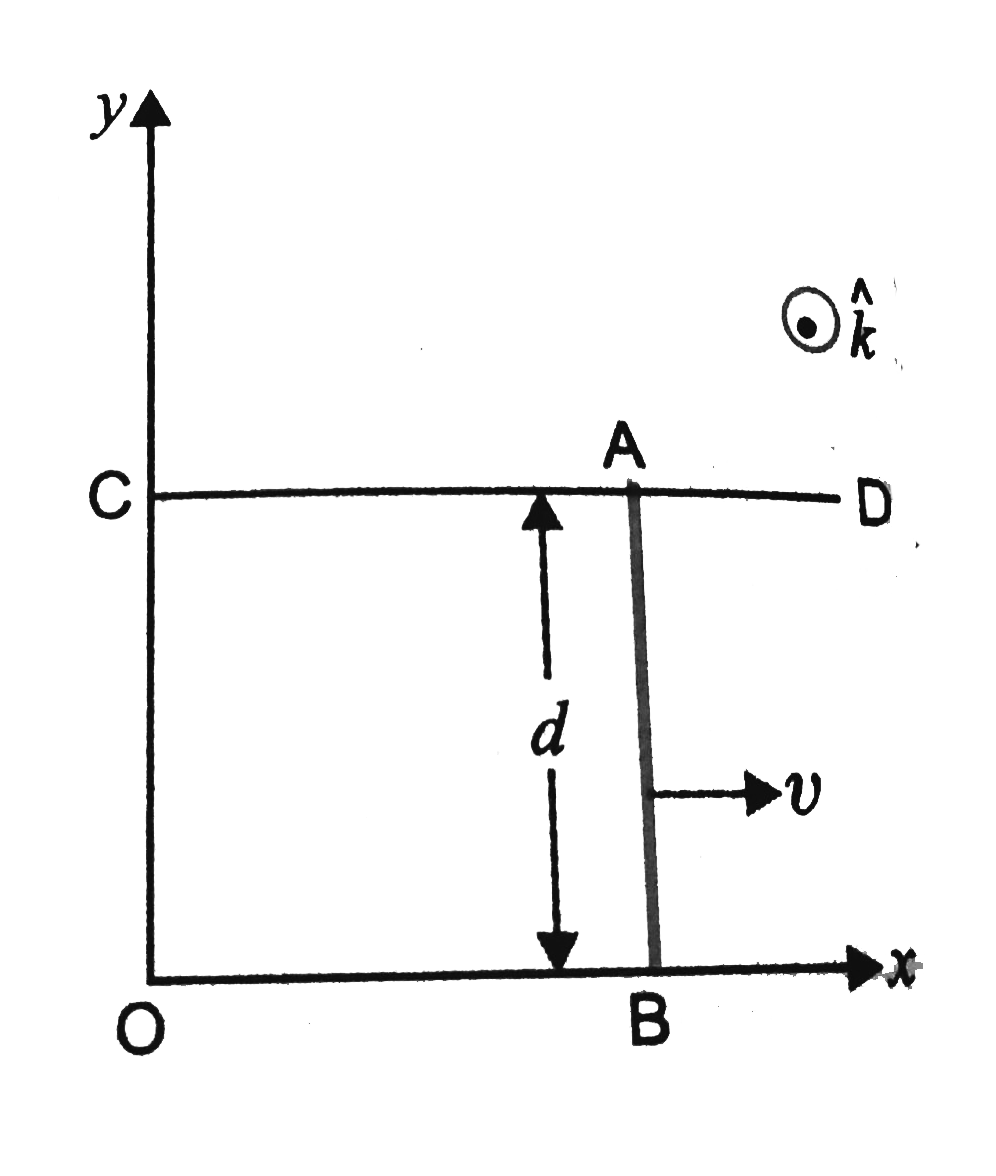
View SolutionA conducting wire XY of mass M and negligible resistance slides smothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field `B=B(t)hatk`
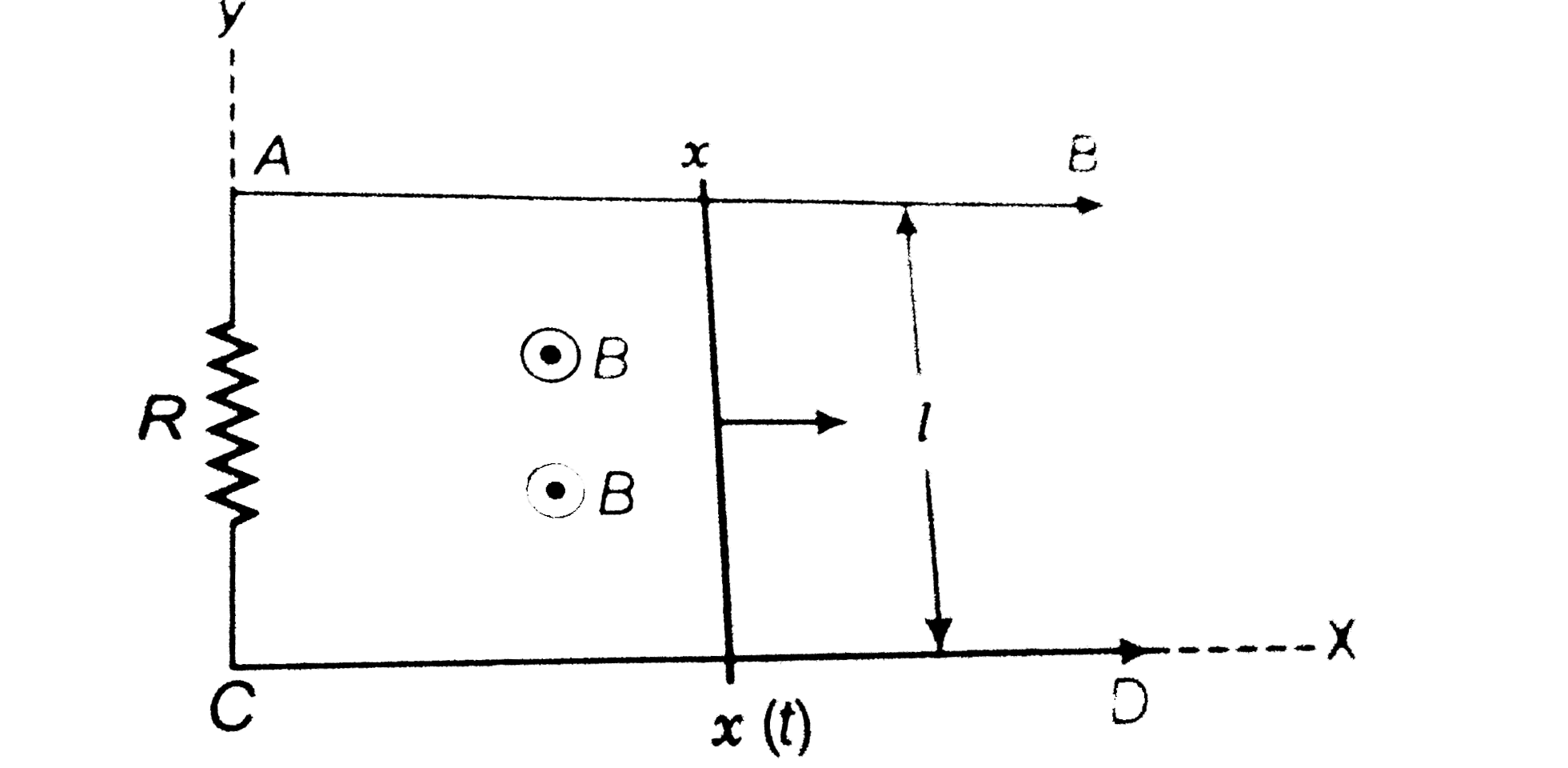
View SolutionODBAC is a fixed rectangular conductor of negligible resistance (C0 is not connected) and 0P is a conductor which clockwise with an angular velocity `omega` (figure). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electirc contact with ABDC. The rotaating conductor has a resistance of `lambda ` per unit length. Find the current in the rotating conductor, as it rotates by `180^@`.
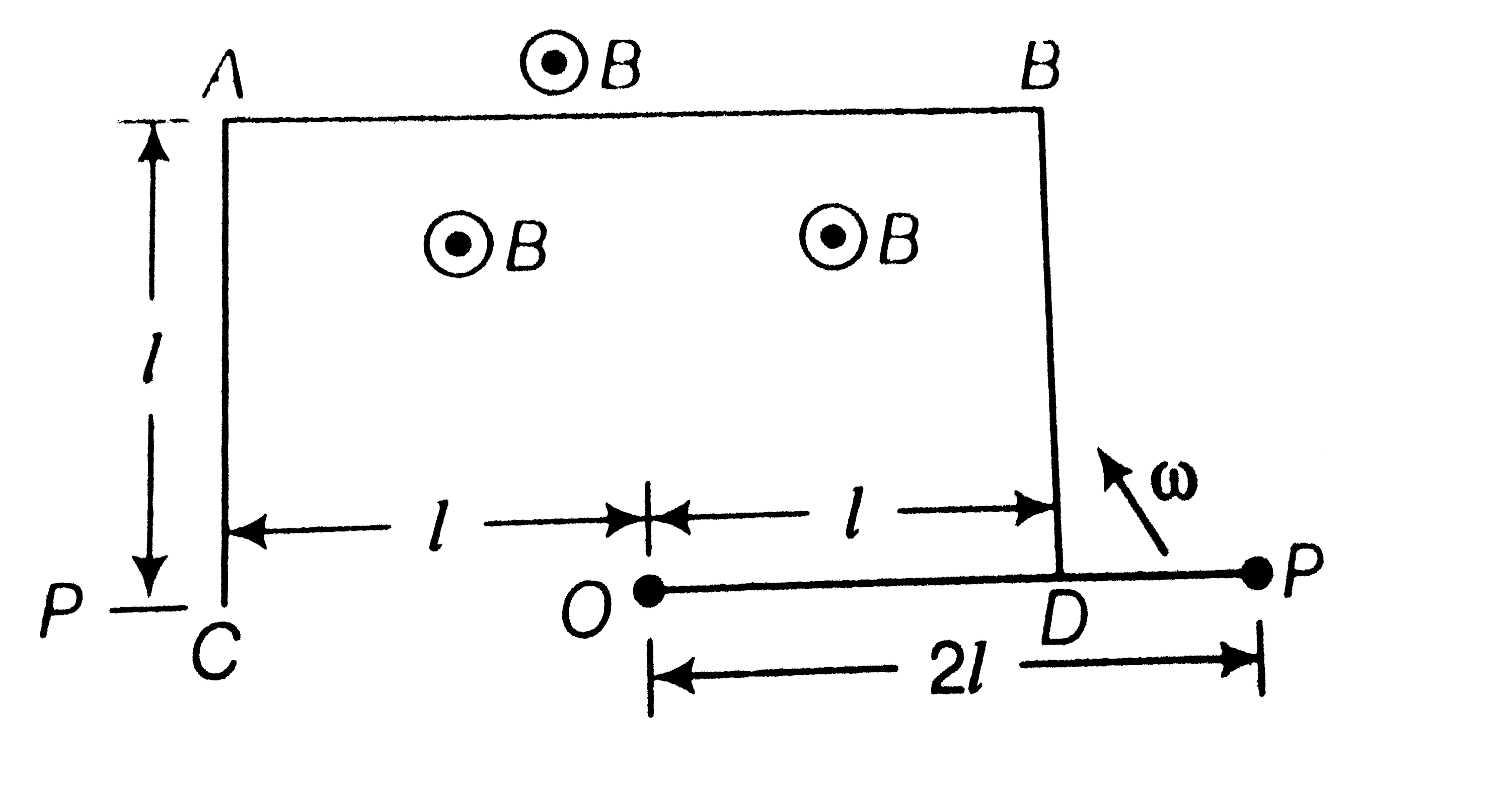
View SolutionConsider an infinitely long wire carrying a current I (t),
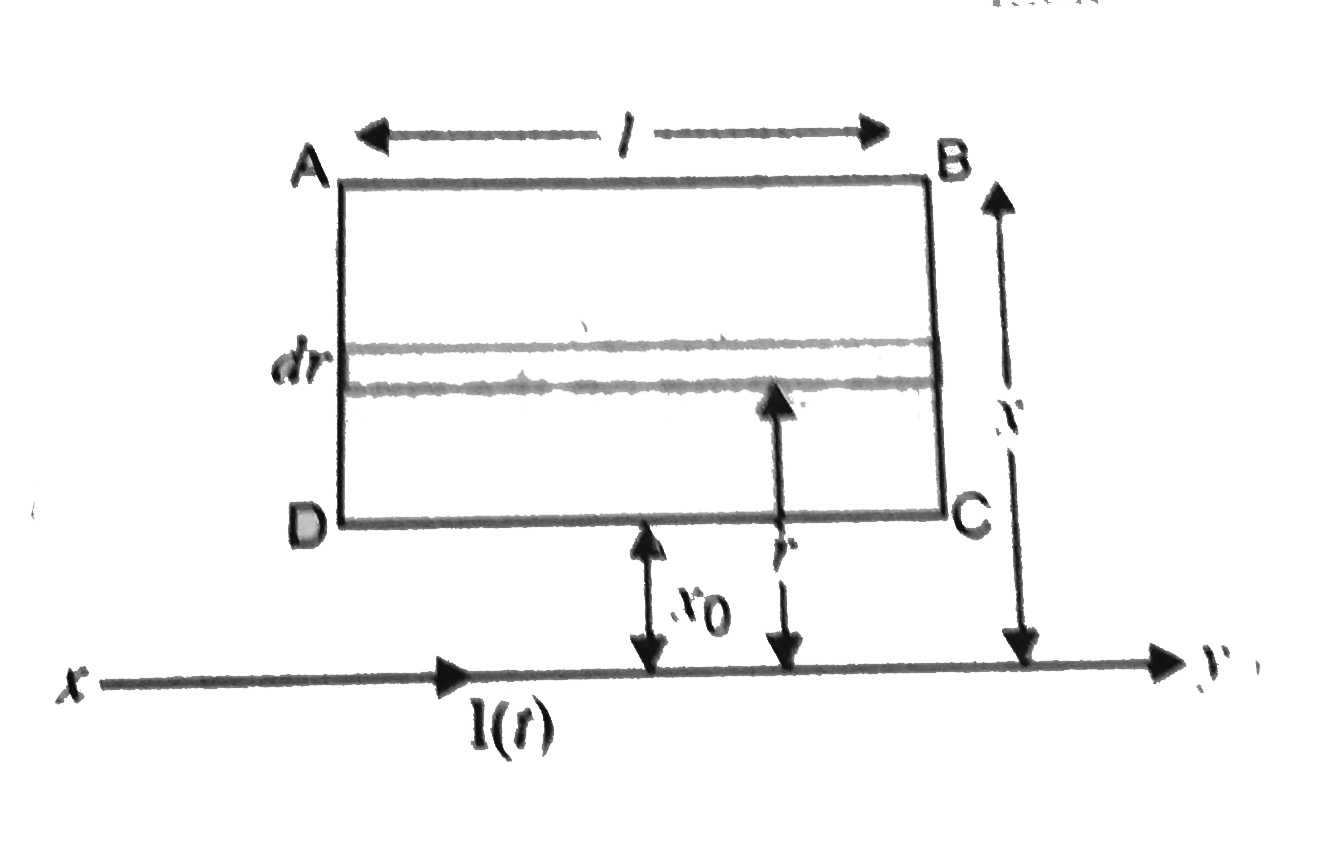
With `(dI)/(dt) = lambda` = constant . Find the current produced in the rectangular loop of wire ABCD if its resistance is R, Fig
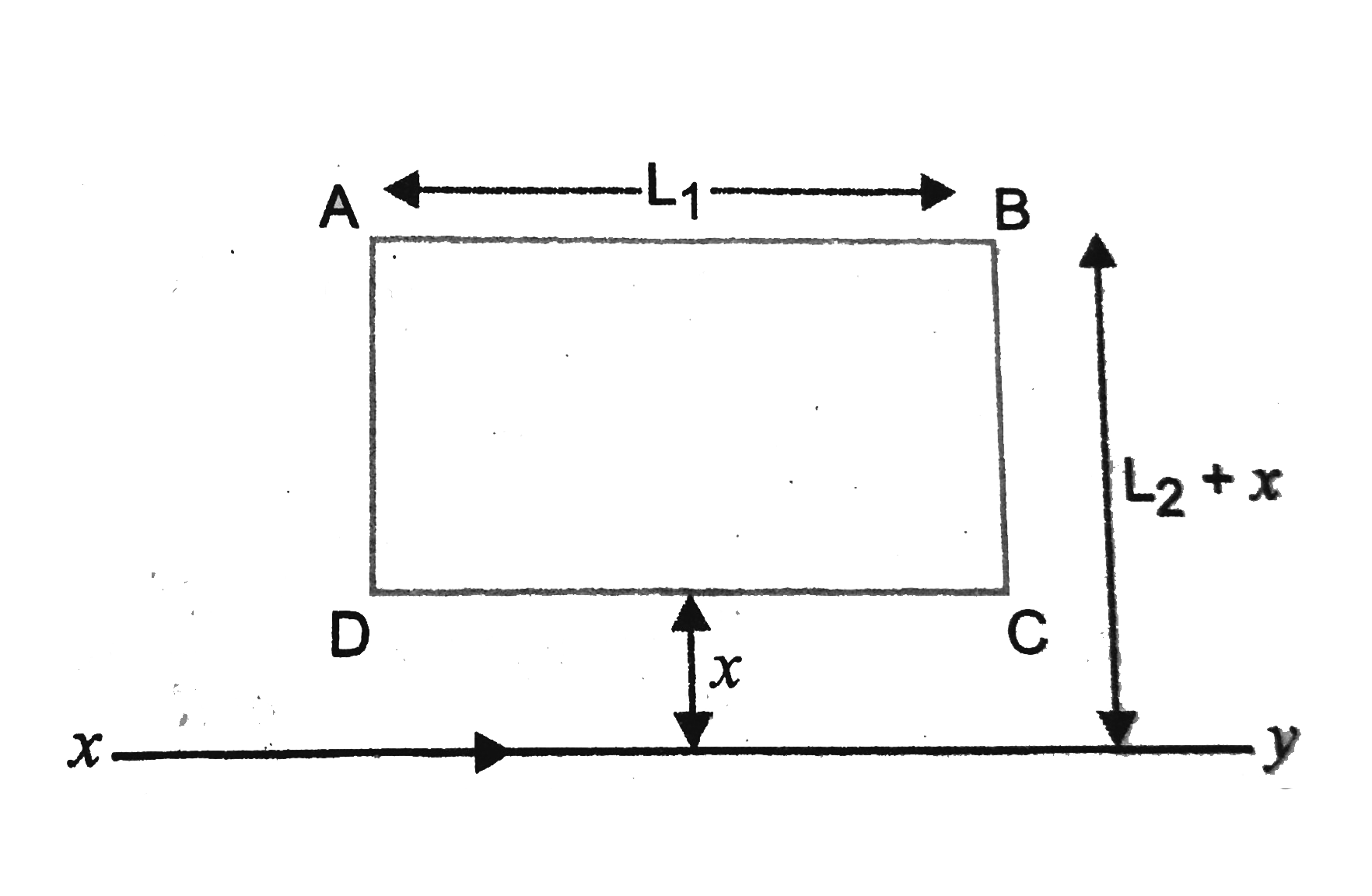
View SolutionA rectangular loop of wire ABCD is kept close to an infinitely long wire carring a current I (t) `= I_(0) (1 = t//T)` for `0 le t le` and I (0) for t gt T, Fig. Find the total charges passing through a given point in the loop, in time T. resistance of the loop is R
View SolutionA magnetic field B is confined to a region `r le` a and points out of the paper (the z-axis), r = 0 being the centre of the cicular region. A charged ring (charge = Q) of radius b,bgt a and mass m lie in the x-y plane with its centre at origin. The ring is free to rotate and is at rest. The magnetic field is brougth to zero in time `Delta t`. Find the angular velocity `omega or the ring after the field vanishes.
View SolutionA rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle `theta` with respect to the horiaontal, Fig. The circuit is closed through a perfert conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.
View SolutionFind the current in the sliding rod AB (resistance = R) for the arranged shown in Fig. B is constant and is out of the paper. Paralllel wires have no resistance. `upsilon` is constant. Switch is closed at time t = 0.
View SolutionFind the current in the sliding rod AB (resistance = R) for the arranged shown in Fig. B is constant and is out of the paper. Paralllel wires have no resistance. `upsilon` is constant. Switch is closed at time t = 0.
View SolutionA metallic ring of field. If z is the radius l (ring being horizontal is falling under gravity in a region haivng a magnetic field. If z is the vertical direction, the z-component of magnetic field is `B_(z) = B_(0) (1 + lambda z)`. If R the resistance of the ring and if the ring falls with a velocity `upsilon`, find the energy lost in the resistance If the ring has reached a constant velocity, use the conservation of energy to determine `upsilon` in terms of m, B, `lambda` and acceleration due to gravity g.
View SolutionA long solenoid 'S' has 'n' turns per meter, with diameter 'a'. At the centre of this coil, we place a smallar coil of 'N' tunrs and diameter 'b' (where b lt a). If the current in the solenoid increase linearly with time, what is the induced emf apperaing in the smaller coil. Plot graph showing nature of variation in emf, if current varies as a function of `mt^(2) + C`.
View Solution
Electromagnetic Induction questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of NCERT PHYSICS (HINGLISH) of Class 12