Complete Solutions to Exercise of chapter સંબંધ અને વિધેય of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | સંબંધ અને વિધેય |
| NCERT | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
નીચે આપેલ સંબંધો પૈકી પ્રત્યેક માટે તે સ્વવાચક, સંમિત અથવા પરંપરિત છે કે નહિ તે ચકસો. `A = {1,2,3, ……13,14}`, `R={(x,y) : 3x-y=0}`
View Solutionનીચે આપેલ સંબંધો પૈકી પ્રત્યેક માટે તે સ્વવાચક, સંમિત અથવા પરંપરિત છે કે નહિ તે ચકસો. `N` પર સંબંધ `R={(x,y) : y = x + 5` અને `x < 4`}`
View Solutionનીચે આપેલ સંબંધો પૈકી પ્રત્યેક માટે તે સ્વવાચક, સંમિત અથવા પરંપરિત છે કે નહિ તે ચકસો. `A={1,2,3,4,5,6}`, `R={(x,y) : y` એ `x` વડે વિભાજ્ય છે.}
View Solutionનીચે આપેલ સંબંધો પૈકી પ્રત્યેક માટે તે સ્વવાચક, સંમિત અથવા પરંપરિત છે કે નહિ તે ચકસો. Z પરનો સંબંધ `R = {(x,y) : x - y` એ પૂર્ણાક છે}`
View Solutionકોઇ ચોક્ક્સ સમયે કોઇ એક નગરમાં વસતા મનુષ્યોના ગણ A પર વ્યાખ્યાયિત સંબંધ `R = {(x, y) : x` અને `y` એક જ સ્થળે કામ કરે છે.}`
View Solutionકોઇ ચોક્ક્સ સમયે કોઇ એક નગરમાં વસતા મનુષ્યોના ગણ A પર વ્યાખ્યાયિત સંબંધ `R = {(x, y) : x` અને `y` એક જ વિસ્તારમાં રહે છે..}`
View Solutionકોઇ ચોક્ક્સ સમયે કોઇ એક નગરમાં વસતા મનુષ્યોના ગણ A પર વ્યાખ્યાયિત સંબંધ `R = {(x, y) : x` ની ઊંચાઇ y ની ઊંચાઇ કરતા બરાબર 7 સેમી વધારે છે.`}`
View Solutionકોઇ ચોક્ક્સ સમયે કોઇ એક નગરમાં વસતા મનુષ્યોના ગણ A પર વ્યાખ્યાયિત સંબંધ `R = {(x, y) : x` એ `y` ની પત્ની છે.}`
View Solutionકોઇ ચોક્ક્સ સમયે કોઇ એક નગરમાં વસતા મનુષ્યોના ગણ A પર વ્યાખ્યાયિત સંબંધ `R = {(x, y) : x` એ `y` ની પિતા છે.}`
View Solutionસાબિત કરો કે વાસ્તવિક સંખ્યાઓના ગણ R પર `S = {(a, b) : a lt b^(2)}` વડે વ્યાખ્યાયિત સંબંધ S. સ્વવાચક, સંમિત અને પરંપરિત સંબંધ પૈકી એક પણ નથી.
View Solutionગણ `{1,2,3,4,5,6}` પર વ્યાખ્યાયિત સંબંધ `R = {(a,b) : b = a+1}` સ્વવાચક, સંમિત કે પરંપરિત છે કે નહી તે ચકાસો.
View Solutionસાબિત કરો કે R પર વ્યાખ્યાયિત સંબંધ `S = {(a, b) : a lt b}` એ પરંપરિત છે, પરંતુ સંમિત અને સ્વવાચક સંબંધ નથી.
View Solutionગણ R પર વ્યાખ્યાયિત સંબંધ `R = {(a,b) : aleb^3}` સ્વવાચક, સંમિત કે પરંપરિત છે કે નહી તે ચકાસો.
View Solutionસાબિત કરો કે ગણ {1, 2, 3} પર વ્યાખ્યાયિત સંબંધ `R = {(1, 2), (2, 1)}` સંમિત છે પરંતુ સ્વવાચક કે પરંપરિત સંબંધ નથી.
View Solutionકોલેજની પુસ્તકાલયમાં રહેલા પુસ્તકોનો ગણ A હોય તથા સંબંધ `R={(x,y)` : x અને y ના પૃષ્ઠોની સંખ્યા સમાન છે.} હોય તો બતાવો કે સંબંધ R સામ્ય સંબંધ છે.
View Solutionગણ `A={{1,2,3,4,5}` પર સંબંધ `R={(a,b) : |a-b|` યુગ્મ પૂર્ણાંક છે.} સાબિત કરો કે R એ સામ્ય સંબંધ છે. સાબિત કરો કે `{1,2,3}` ના બધા જ ઘટકો એકબીજા સાથે સંબંધ R ધરાવે છે અને `{2,4}`ના બધા જ ઘટકો એકબીજા સાથે સંબંધ R ધરાવે છે, પરંતુ `{1,3,5}` નો એક પણ ઘટક `{2,4}` ના કોઈ પણ ઘટક સાથે સંબંધ ધરાવતો નથી.
View Solutionગણ `A={xinZ, 0 le x le 12}` પર સંબંધ R નીચે મુજબ વ્યાખ્યાયિત છે.`R = {(a,b) : |a-b|` એ 4 નો ગુણાંક છે.}`
View Solutionગણ `A={xinZ, 0 le x le 12}` પર સંબંધ R નીચે મુજબ વ્યાખ્યાયિત છે.`R = {(a,b) : |a-b|` એ 4 નો ગુણાંક છે.}`
View Solutionજે (i) સંમિત હોય પરંતુ સ્વવાચક કે પરંપરિત ના હોય. (ii) પરંપરિત હોય પરંતુ સ્વવાચક કે સંમિત ના હોય. , તેવા સંબંધોનાં ઉદાહરણો આપો.
View Solutionસાબિત કરો કે સમતલમાં આવેલાં બિંદુઓના ગણ A પર વ્યાખ્યાયિત સંબંધ `R = {(P, Q):` ઊગમબિંદુથી બિંદુ P નું અંતર એ ઊગમબિંદુથી બિંદુ Q ના અંતર જેટલું જ છે} હોય, તો R એ સામ્ય સંબંધ છે. સાબિત કરો કે ઊગમબિંદુ સિવાયના બિંદુ P સાથે સંબંધ R ધરાવતા બધાં જ બિંદુઓનો ગણ એ P માંથી પસાર થતું અને ઊગમબિંદુ કેન્દ્રવાળું વર્તુળ છે.
View Solutionસંબંધ R એ તમામ બહુકોણ ધરાવતો ગણ A માટે નીચે મુજબ વ્યાખ્યાયિત છે. `R={(P_1, P_2)` : `P_1` અને `P_2` ની બાજુઓ ની સંખ્યા સમાન છે.} સાબિત કરો કે, સંબંધ R સામ્ય સંબંધ છે. તથા 3,4,5 લંબાઈની બાજુઓ વાળા કાટકોણ ત્રિકોણ સાથે સંબંધ R ધરાવતા ગણ A ના તમામ ઘટકોનો ગણ શું મળશે ?
View Solutionજે. (iii) સ્વવાચક અને સંમિત હોય પરંતુ પરંપરિત ના હોય. (iv) સ્વવાચક અને પરંપરિત હોય પરંતુ સંમિત ના હોય. તેવા સંબંધોનાં ઉદાહરણો આપો
View Solutionગણ {1, 2, 3, 4} પર સંબંધ R એ `R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}` દ્વારા આપેલ છે
View Solutionસંબંધ R એ ગણ N પર `R = {(a, b) : a = b – 2, b gt 6}` દ્વારા આપેલ છે.
View Solutionધારો કે `R*` તમામ શૂન્યતર વાસ્તવિક સંખ્યાઓનો ગણ છે. સાબિત કરો કે વિધેય `f : R* rarr R*`, `f(x) = 1/x` વડે વ્યાખ્યાયિત વિધય f એક-એક અને વ્યાપ્ત છે. જો પ્રદેશ `R*` ના બદલે N લેવામાં આવે અને સહપ્રદેશ `R*` જ રહે તો શું આ પરિણામ સત્ય રહેશે ?
View Solutionનીચે આપેલ વિધેયો એક-એક અથવા વ્યાપ્ત અથવા બંને ગુણધર્મ ધરાવતાં વિધેયો છે કે નહિ તે ચકાસો : `f : N rarr N`, `f(x) = x^(2)`
View Solutionનીચે આપેલ વિધેયો એક-એક અથવા વ્યાપ્ત અથવા બંને ગુણધર્મ ધરાવતાં વિધેયો છે કે નહિ તે ચકાસો : `f : Z rarr Z`, `f(x) = x^(2)`
View Solutionનીચે આપેલ વિધેયો એક-એક અથવા વ્યાપ્ત અથવા બંને ગુણધર્મ ધરાવતાં વિધેયો છે કે નહિ તે ચકાસો : `f : R rarr R`, `f(x) = x^(2)`
View Solutionનીચે આપેલ વિધેયો એક-એક અથવા વ્યાપ્ત અથવા બંને ગુણધર્મ ધરાવતાં વિધેયો છે કે નહિ તે ચકાસો : `f : N rarr N`, `f(x) = x^(3)`
View Solutionનીચે આપેલ વિધેયો એક-એક અથવા વ્યાપ્ત અથવા બંને ગુણધર્મ ધરાવતાં વિધેયો છે કે નહિ તે ચકાસો : `f : Z rarr Z`, `f(x) = x^(3)`
View Solutionસાબિત કરો કે `f : R rarr R`, `f (x) = [x]`દ્વારા વ્યાખ્યાયિત મહત્તમ પૂર્ણાક વિધેય (Greatest integer function) એક-એક પણ નથી અને વ્યાપ્ત પણ નથી. અહીં, [x] એ x થી નાના અથવા x ને સમાન તમામ પૂર્ણાકોમાં મહત્તમ પૂર્ણાક દર્શાવે છે. બીજા શબ્દોમાં x થી અધિક નહિ તેવા પૂર્ણાકોમાં સૌથી મોટો પૂર્ણાક x છે.
View Solutionસાબિત કરો કે માનાંક વિધેય `f : R rarr R`, `f (x) = |x|` દ્વારા વ્યાખ્યાયિત વિધેય એક-એક નથી અને વ્યાપ્ત પણ નથી. જો x ધન અથવા શૂન્ય (અનૃણ) હોય, તો `|x| = x` અને x ઋણ હોય, તો `|x| = -x`.
View Solutionસાબિત કરો કે ચિહ્ન વિધેય (Signum Function) `f : R rarr R`, `f (x)= {( x/|x| , x ne 0), (0, x = 0 ):} ` દ્વારા વ્યાખ્યાયિત વિધેય એક-એક નથી અને વ્યાપ્ત પણ નથી.
View Solution`A = {1, 2, 3}`, `B = {4, 5, 6, 7}` છે અને વિધેય `f : A rarr B`, `f = {(1, 4), (2, 5), (3, 6)}` દ્વારા વ્યાખ્યાયિત છે. સાબિત કરો કે f એક-એક છે.
View Solutionનીચે આપેલ પ્રત્યેક પ્રશ્નમાં આપેલાં વિધેય એક-એક છે કે નહિ, વ્યાપ્ત છે કે નહિ અથવા એક-એક અને વ્યાપ્ત છે કે નહિ તે નક્કી કરો. તમારા જવાબનું સમર્થન કરો : `f: R rarr R` એ `f (x) = 3 - 4x` દ્વારા વ્યાખ્યાયિત વિધેય છે.
View SolutionA અને B આપેલ ગણ છે. સાબિત કરો કે `f : A ** B - B ** A`, `f ((a, b)) = (b, a)` દ્વારા વ્યાખ્યાયિત વિધેય એક-એક અને વ્યાપ્ત છે.
View Solution`f : NrarrN`, `f(n)={(n/2), n` યુગ્મ`)`, `((n + 1)/2, n` અયુગ્મ`):}` f` એક-એક છે?f વ્યાપ્ત છે ? ચકાસો.
View Solution`A = R- {3}` અને `B = R- {1}` છે. `f (x) = (x-2)/(x-3)` દ્વારા વ્યાખ્યાયિત વિધેય `f : A rarr B` નો વિચાર કરો. શું f એક-એક અને વ્યાપ્ત છે ? તમારા જવાબનું સમર્થન કરો.
View Solution`f : R rarr R`, `f (x) = x^(4)` દ્વારા વ્યાખ્યાયિત વિધેય છે.
View Solutionવિધેય `f: R rarr R`, `f(x) = 3x` દ્વારા વ્યાખ્યાયિત છે.
View Solutionધારો કે `f = {1, 3, 4} rarr {1, 2, 5}` અને `g = {1, 2, 5} rarr {1, 3}` એ `f = {(1, 2), (3, 5), (4, 1)}` અને `g = {(1, 3), (2, 3), (5, 1)}` દ્વારા વ્યાખ્યાયિત વિધેયો છે. gof શોધો.
View Solutionધારો કે વિધેયો f, g અને h એ R થી R આપેલાં છે. સાબિત કરો કે, `(f + g)oh = foh + goh`
`(f * g)oh = (foh) * (goh)`
View Solutionનીચે આપેલા વિધેયો માટે `gof` અને `fog` શોધો. `f(x) = |x|`, `g(x) = |5x - 2|`
View Solutionનીચે આપેલા વિધેયો માટે `gof` અને `fog` શોધો. `f(x) = 8x^3`, `g(x) = x^(1/3)`
View Solutionનીયોના આપેલા પ્રશ્ર્ન નંબર 9 થી 14 ની માગ્યા મુજખ ગણતરી કરી જવાખ આપો ( દરેકના 3 ગુણ છે.)
જો `f(x) =(4x+3)/(6x-4), x!=2/3` હોય,તો ખધા જ `x=2/3` માટે સાખિત કરો કે `(fof) (x)=x` અને f નું પ્રતિવિધેય શું છે?
View Solutionનીચે આપેલા વિધેય માટે ચકાસો કે પ્રતિવિધેયનું અસ્તિત્વ છે કે નહી જો પ્રતિવિધેયનું અસ્તિત્વ હોય તો તે શોધો. : `f : {1,2,3,4} rarr {10}` `f = {(1,10), (2,10), (3,10), (4,10)}`
View Solutionનીચે આપેલાં વિધેયોનાં પ્રતિવિધેય મળી શકશે ? કારણ સહિત નિર્ણય કરો. `g: {5, 6, 7, 8} rarr {1, 2, 3, 4}`, `g: {(5, 4), (6, 3), (7, 4), (8, 2)}`
View Solutionનીચે આપેલાં વિધેયોનાં પ્રતિવિધેય મળી શકશે ? કારણ સહિત નિર્ણય કરો. `h : {2, 3, 4, 5} rarr {7, 9, 11, 13}`, `h : {(2, 3), (3, 3), (4, 11), (5, 13)}`
View Solutionસાબિત કરો કે `f : [-1, 1] rarr R`, `f (x) = x/(x+2)` દ્વારા વ્યાખ્યાયિત વિધેય એક-એક છે. વિધેય `f: [-1, 1] rarr f` નો વિસ્તાર `f (x) = x/(x+2)`, તો નું પ્રતિવિધેય શોધો. સૂચન : f ના વિસ્તારમાં આવેલ y ને સંગત કોઈક `x ∈[-1, 1]` માટે `y = f (x) = x/(x+2)`, એટલે કે, `x = (2y)/(1-y)`
View Solutionજો `f : R rarr R`, `f(x) = 4x + 3` તો સાબિત કરો કે f વ્યસ્ત સંપન્ન વિધેય છે `f` નું પ્રતિવિધેય શોધો.
View Solutionનીયોના આપેલા પ્રશ્ર્ન નંબર 9 થી 1 ની માગ્યા મુજખ ગણતરી કરી જવાખ આપો ( દરેકના 3 ગુણ છે.)
વિધેય `f: R^(+) to [4, infty]`, `f(x) = x^(2) +4` દ્વારા વ્યાખ્યાયિત છે. સાબિત કરો કે f વ્યસ્ત સપંન્ન છે. અને f નું પ્રતિવિધેય `f^(-1)` એ `f^(-1) (y) = \sqrt{y-4}` દ્વારા દર્શાવાય છે. અત્રે`R^(+)` એ તમામ અનુણ વાસ્તવિક સંખ્યાઓનો ગણ છે.
View Solution`f : R_+ rarr [-5, oo)`, `f(x) = 9x^2 + 6x - 5` સાબિત કરો કે f વ્યસ્ત સંપન્ન વિધેય છે અને `f^(-1)((y)) = ((sqrt(y+6)-1)/3)`.
View Solutionવિધેય `f: X rarr Y` વ્યસ્તસંપન્ન છે. સાબિત કરો કે `f` નું પ્રતિવિધેય અનન્ય છે. (સૂચન : ધારો કે `g_1`અને `g_2`, બંને વિધેય `f` નાં પ્રતિવિધેયો છે. તેથી પ્રત્યેક `y ∈ Y` માટે `(fog_1)(y) = I_Y(y) = (fog_2)(y)`. વિધેય f એક-એક છે, તે સત્યનો ઉપયોગ કરો.
View Solutionજો `f : {1,2,3} rarr {a,b,c}` તથા `f(1) = a`, `f(2) = b`, `f(3) = c` તો `f^(-1)` શોધો તથા સાબિત કરો કે `(f^(-1))^(-1) = f`.
View Solutionજો `f : x rarr y` વ્યસ્ત સંપન્ન વિધેય હોય તો સાબિત કરો કે `f^(-1)` નું પ્રતિવિધેય f છે. એટલે કે = `(f^(-1))^(-1)` = f
View Solutionનીયેના બહુવિકલ્પ પ્રશ્નોના જવાબ માટે સાયો વિકલ્પ પસંદ કરો
જો વિધેચ `f : R to R ` એ `f(x)=(3-x^(3))^(1/3)` દ્વારા આપેલ છે, `(fof) (x)` ........ તો છે
View Solutionજો `f : R - {-4/3} rarr R, f(x) = (4x)/(3x+4)` હોય તો `f` ના પ્રતિવિધેય `g : R_f rarr R - {-4/3}` માટે `g(y)`= ……..
View Solutionનીચે પ્રમાણે વ્યાખ્યાયિત કરેલ પ્રત્યેક ક્રિયા * એ ક્રિક્રિયા છે કે નહિ તે નક્કી કરો. જે પ્રશ્નમાં * ક્રિક્રિયા ન હોય, તેના માટે કારણ આપો : `* Z^(+)` પર, `a * b = a -b` દ્વારા વ્યાખ્યાયિત છે.
View Solutionનીચે આપેલ યોગ્ય પ્રદેશ પર `**` એ વ્યાખ્યાયિત છે. આ દિક્ ક્રિયા છે કે નહી તે નક્કી કરો. : `Z^+` પર `**` એ `a**b = ab`
View Solutionનીચે આપેલ યોગ્ય પ્રદેશ પર `**` એ વ્યાખ્યાયિત છે. આ દિક્ ક્રિયા છે કે નહી તે નક્કી કરો. : `R` પર `**` એ `a**b = ab^2`
View Solutionનીચે આપેલ યોગ્ય પ્રદેશ પર `**` એ વ્યાખ્યાયિત છે. આ દિક્ ક્રિયા છે કે નહી તે નક્કી કરો. : `Z^+` પર `**` એ `a**b = |a-b|`
View Solutionનીચે આપેલ યોગ્ય પ્રદેશ પર `**` એ વ્યાખ્યાયિત છે. આ દિક્ ક્રિયા છે કે નહી તે નક્કી કરો. : `Z^+` પર `**` એ `a**b = a`
View Solutionનીચે આપેલી દિકક્રિયા સમક્રમી છે કે નહી ? જૂથના નિયમનું પાલન કરે છે કે નહી ? : Z પર `a**b = a - b`
View Solutionનીચે આપેલી દિકક્રિયા સમક્રમી છે કે નહી ? જૂથના નિયમનું પાલન કરે છે કે નહી ? : `Q` પર `a**b = ab + 1`
View Solutionનીચે આપેલી દિકક્રિયા સમક્રમી છે કે નહી ? જૂથના નિયમનું પાલન કરે છે કે નહી ? : Q પર `a**b = (ab)/2`
View Solutionનીચે આપેલી દિકક્રિયા સમક્રમી છે કે નહી ? જૂથના નિયમનું પાલન કરે છે કે નહી ? : Z પર `a**b = 2^(ab)`
View Solutionનીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત પ્રત્યેક ક્રિયા * માટે નક્કી કરો કે તે ક્રિક્રિયા છે કે નહિ. જો તે ક્રિક્રિયા હોય, તો એ સમક્રમી છે કે નહિ અથવા જૂથના નિયમનું પાલન કરે છે કે નહિ તે નક્કી કરો : `Z^(+)` પર વ્યાખ્યાયિત `a * b = a^(b)`
View Solutionનીચે આપેલી દિકક્રિયા સમક્રમી છે કે નહી ? જૂથના નિયમનું પાલન કરે છે કે નહી ? : `R - {-1}` પર `a**b = a/(b + 1)`
View Solutionગણ `{1,2,3,4,5}` પર `^^` એ `a ^^ b = min (a,b)`, (a તથા b પૈકી નાની સંખ્યા) વડે વ્યાખ્યાયિત છે. `^^` માટે ક્રિયા કોષ્ટક બનાવો.
View Solutionગણ `{1,2,3,4,5}` પર `**` એ નીચે મુજબ વ્યાખ્યાયિત છે. નીચે આપેલ ક્રિયા કોષ્ટક પરની નીચેના પ્રશ્નોના જવાબ આપો.: ગણતરી કરો : `(2 ** 3) ** 4` અને `2 ** (3 ** 4)`
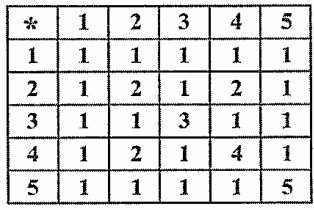
View Solutionધારો કે ગણ {1, 2, 3, 4, 5} પર ક્રિક્રિયા `*`, નીચે આપેલા ગુણાકાર કોષ્ટક (કોષ્ટક 1.2) દ્વારા વ્યાખ્યાયિત કરેલ છે :`*` સમક્રમી છે ?
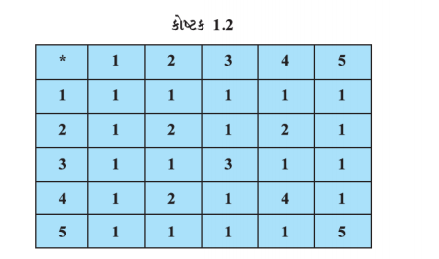
View Solutionગણ `{1,2,3,4,5}` પર `**` એ નીચે મુજબ વ્યાખ્યાયિત છે. નીચે આપેલ ક્રિયા કોષ્ટક પરની નીચેના પ્રશ્નોના જવાબ આપો.: ગણતરી કરો : `(2 ** 3) ** (4 ** 5)`
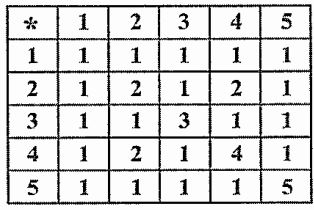
View Solutionગણ `{1,2,3,4,5}` પર `**` એ `a ** b = (a,b)`, નો ગુ.સા.અ. વડે વ્યાખ્યાયિત છે. પ્રશ્ન -4 માં આપેલ `**` સાથે સરખાવો અને તમારો જવાબ લખો.

View SolutionN પર `**` એ `a ** b` = a અને b નો લ.સા.અ. વડે વ્યાખ્યાયિત દિકક્રિયા છે. નીચેના પ્રશ્નોના જવાબ લખો. : `5 ** 7`, `20 ** 16` શોધો.
View SolutionN પર `**` એ `a ** b` = a અને b નો લ.સા.અ. વડે વ્યાખ્યાયિત દિકક્રિયા છે. નીચેના પ્રશ્નોના જવાબ લખો. : `**` સમક્રમી છે ?
View SolutionN પર `**` એ `a ** b` = a અને b નો લ.સા.અ. વડે વ્યાખ્યાયિત દિકક્રિયા છે. નીચેના પ્રશ્નોના જવાબ લખો. : `**` એ જૂથના નિયમનું પાલન કરે છે.
View SolutionN પર `**` એ `a ** b` = `a` અને `b` નો લ.સા.અ. વડે વ્યાખ્યાયિત દિકક્રિયા છે. નીચેના પ્રશ્નોના જવાબ લખો. : `**` એ માટે તટસ્થ ઘટક શોધો.
View SolutionN પર `**` એ `a ** b` = `a` અને `b` નો લ.સા.અ. વડે વ્યાખ્યાયિત દિકક્રિયા છે. નીચેના પ્રશ્નોના જવાબ લખો. : દિકક્રિયા માટે `N` ના ક્યા ઘટકો વ્યસ્ત સંપન્ન છે ?
View SolutionN પર `**` એ `a ** b` = `a` અને `b` નો લ.સા.અ. વડે વ્યાખ્યાયિત દિકક્રિયા છે. નીચેના પ્રશ્નોના જવાબ લખો. : `**` એ માટે તટસ્થ ઘટક શોધો.
View Solutionગણ N પર `**` એ `a ** b` = a તથા b નો ગુ.સા.અ. વડે વ્યાખ્યાયિત છે. `**` સમક્રમી છે ? જૂથના નિયમનું પાલન કરે છે ? એકમ ઘટકનું અસ્તિત્વ છે ?
View Solutionસંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે :દ્રિક્રક્રિયાઓ સમક્રમી છે અને કઈ ક્રિયાઓ જૂથના નિયમનું પાલન કરે છે તે શોધો. `a *b = a - b`
View Solutionસંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે : દ્રિક્રક્રિયાઓ સમક્રમી છે અને કઈ ક્રિયાઓ જૂથના નિયમનું પાલન કરે છે તે શોધો. `a*b =a^(2) + b^(2)`
View Solutionસંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે : દ્રિક્રક્રિયાઓ સમક્રમી છે અને કઈ ક્રિયાઓ જૂથના નિયમનું પાલન કરે છે તે શોધો. `a *b = a + ab`
View Solutionસંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે : દ્રિક્રક્રિયાઓ સમક્રમી છે અને કઈ ક્રિયાઓ જૂથના નિયમનું પાલન કરે છે તે શોધો. `a *b = (a - b)^(2)`
View Solutionસંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે : દ્રિક્રક્રિયાઓ સમક્રમી છે અને કઈ ક્રિયાઓ જૂથના નિયમનું પાલન કરે છે તે શોધો. `a *b = (ab)/4`
View Solutionસંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે : દ્રિક્રક્રિયાઓ સમક્રમી છે અને કઈ ક્રિયાઓ જૂથના નિયમનું પાલન કરે છે તે શોધો. `a *b = ab^(2)`
View Solutionકઈ દ્રિકક્રિયાઓ માટે તટસ્થ ઘટક પ્રાપ્ય છે ? સંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે :`a *b = a-b`
View Solutionકઈ દ્રિકક્રિયાઓ માટે તટસ્થ ઘટક પ્રાપ્ય છે ? સંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે :`a *b = a^2+b^2`
View Solutionનીચે આપેલાં વિધાનો સત્ય છે કે અસત્ય તે જણાવો. તમારા જવાબની યથાર્થતા ચકાસો : ગણ N પરની કોઈ પણ દ્રિકક્રિયા `*` માટે, `a * a = a`, `forall a ∈ N`.
View Solutionનીચે આપેલાં વિધાનો સત્ય છે કે અસત્ય તે જણાવો. તમારા જવાબની યથાર્થતા ચકાસો : જો `*` N પર સમક્રમી દ્રિકક્રિયા હોય તો `a* (b * c) = (c * b) * a`.
View Solutionકઈ દ્રિકક્રિયાઓ માટે તટસ્થ ઘટક પ્રાપ્ય છે ? સંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે :`a *b = a+ab`
View Solutionકઈ દ્રિકક્રિયાઓ માટે તટસ્થ ઘટક પ્રાપ્ય છે ? સંમેય સંખ્યાઓના ગણ Q પર દ્રિક્રિયા `*` નીચે દર્શાવ્યા પ્રમાણે વ્યાખ્યાયિત છે :`a *b = (a-b)^2`
View Solutionધારો કે W એ પૂર્ણ સંખ્યાઓનો ગણ છે. `f : W rarr W`, `n` અયુગ્મ માટે `f (n) = n -1` દ્વારા વ્યાખ્યાયિત છે અને `n` યુગ્મ માટે `f (n) = n + 1` વ્યાખ્યાયિત કરો. સાબિત કરો કે f એ વ્યસ્ત સંપન્ન છે. `f` નો વ્યસ્ત શોધો.
View Solutionધારો કે, `f : R rarr R`, `f(x) = x^2 -3x +2` તો `f(f(x))` શોધો.
View Solutionનીચે આપેલા પ્રશ્ર્ન નંખર. 9 થી 1 માગ્યા મુજખ ગણતરી કરી જવાખ આપો (દરેક પ્રશ્ર્ન 3 ગુણ છે): સાબિત કરો કે વિધેય `f: R to {x in R: -1 lt x lt 1}, f(x) = x/(1+ |x|)` એક એક અને વ્યાપ્ત છે
View Solutionબતાવો કે વિધેય `f : R rarr R`, `f(x) = x^3` એક-એક છે.
View Solutionવિધેય `f : N rarr Z` અને `g : Z rarr Z` એવા લખો કે જેથી gof એક-એક વિધેય હોય પણ g એક-એક વિધેય ન હોય.
View Solutionવિધેય `f : N rarr N` અને `g : N rarr N` માટે બે ઉદાહરણ આપો કે gof વ્યાપ્ત વિધેય હોય પણ f વ્યાપ્ત ન હોય.
View Solutionધારો કે `x != O/`, x ના બધા ઉપગણોનો ગણ `P(x)` છે. `P(x)` માં વ્યાખ્યાયિત સંબંધ R નીચે મુજબ વ્યાખ્યાયિત છે. `A,B in P(x) _AR_B` = `A sub B` સંબંધ R સામ્ય સંબંધ છે ?
View Solutionનીચે આપેલા પ્રશ્ર્ન નંખર થી ની માગ્યા મુજબ ગણતરી કરી જવાબ આપો
P(X) આચેલ અરિકત્ત ગણ નો ધાતગણ છે. દ્વિકૂકિચા `ast : P(X) times P(X) to એ A ast B= A cap B`, `forall A, B \in P(X)` દ્વારા વ્યાખ્યાચિત છે સાખિત કરો કે એ આ કિચા માટે તટસથ ધટક છે અને `ast` દ્વિકકિચા ને સાપેક્ષ P(X) માં કેવળ X જ વ્યસ્તસંપન્ન છે ..
View Solution
Exercise questions and complete solutions for chapter સંબંધ અને વિધેય of NCERT Maths(Gujarati) of Class 12