Complete Solutions to Example of chapter સદિશ બીજગણિત of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | સદિશ બીજગણિત |
| NCERT | Example |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
દક્ષિણથી પશ્ચિમ તરફ `30^circ` ના ખૂણે 40 કિમીનું સ્થાનાંતર આલેખ દ્વારા દર્શાવો.
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 5 સેકન્ડ
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : `1000 `સેમી^(3)`
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 10 ન્યૂટન
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 30 કિમી/કલાક
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : `10` ગ્રામ/સેમી^(3)
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 20 મી/સે ઉત્તર તરફ
View Solutionઆકૃતિ 10.5 માં કયા સદિશો. સમરેખ.
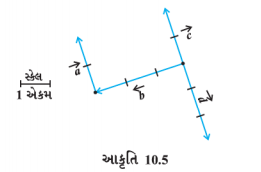
View Solutionઆકૃતિ 10.5 માં કયા સદિશો સમાન.
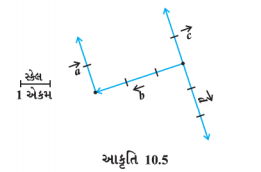
View Solutionઆકૃતિ 10.5 માં કયા સદિશો. સમઉદ્ભવ સદિશો છે?
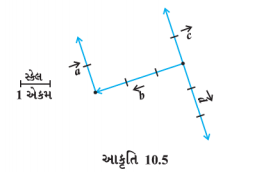
View Solutionબિંદુઓ P અને Q ના સ્થાનસદિશો અનુક્રમે `vec OP = 3 vec a – 2 vec b` છે અને `vec OQ = vec a + vec b` છે. બિંદુઓ `P` અને `Q` ને જોડતા રેખાખંડનું `2:1` ગુણોત્તરમાં. (i) અંતઃવિભાજન અને.
View Solutionબિંદુઓ P અને Q ના સ્થાનસદિશો અનુક્રમે `vec OP = 3 vec a – 2 vec b` છે અને `vec OQ = vec a + vec b` છે. બિંદુઓ `P` અને `Q` ને જોડતા રેખાખંડનું `2:1` ગુણોત્તરમાં . (ii) બહિર્વિભાજન કરતાં બિંદુ R ના સ્થાનસદિશ શોધો.
View Solutionસાબિત કરો કે બિંદુઓ `A (2 hat i - hat j + hat k)`, `B ( vec i - 3 vec j - 5 vec k)`, `C (3 vec i - 4 vec j – 4 vec k)` કાટકોણ ત્રિકોણનાં શિરોબિંદુઓ છે.
View Solutionજો `vec a = 5 hat i - hat j - 3 hat k` અને `vec b = hat i + 3 hat j - 5 hat k`હોય, તો દર્શાવો કે સદિશો `vec a + vec b` છે અને `vec a - vec b` પરસ્પર લંબ છે.
View Solutionસદિશ `vec a = 2 hat i+ 3 hat j+ 2 hat k` નો સદિશ `vec b = hat i+ 2 hat j + hat k` પરનો પ્રક્ષેપ શોધો.
View Solutionકોઈ પણ બે સદિશો `vec a` અને `vec b` માટે સાબિત કરો કે આપણને હંમેશાં `|vec a*vec b| le |vec a| |vec b|` મળે છે.
View Solutionકોઈ પણ બે સદિશો `vec a` અને `vec b` માટે દર્શાવો કે `|vec a+ vec b| le |vec a| +|vec b|`
View Solutionસાબિત કરો કે બિંદુઓ `A (-2 hat i + 3 hat j + 5 hat k)`, `B (hat i + 2 hat j + 3 hat k)` અને `C (7 hat i – hat k)` સમરેખ છે.
View Solutionજો `vec a = hat i +hat j + hat k` , `vec b =hat i + 2 hat j + 3 hat k` હોય, તો સદિશ `(vec a+ vec b)` અને `(vec a- vec b)` બંનેને લંબ એકમ સદિશ શોધો.
View SolutionXY સમતલના બધા જ એકમ સદિશો લખો.
View Solutionસદિશો `vec a, vec b` અને `vec c` માટે `|vec a| = 3, |vec b| = 4, |vec c| = 5` છે અને તેમનામાંથી પ્રત્યેક સદિશ બાકીના બે સદિશના સરવાળાને લંબ હોય, તો `|vec a + vec b+ vec c|` શોધો.
View Solutionત્રણ સદિશો `vec a`, `vec b` અને `vec c` શરત `vec a+ vec b + vec c = vec 0` નું પાલન કરે છે. જો `|vec a|= 1`, `|vec b| = 4` અને `|vec c| = 2` હોય, તો રાશિ `mu = vec a*vec b + vec b*vec c + vec c*vec a` નું મૂલ્ય મેળવો.
View Solutionનીયે આપેલા થી સુધીના પ્રશ્ર્નોની ગણતરી કરી ટૂંકમાં જવાબ આપો (દરેક પ્રશ્ર્ના 2 ગુણ છે) પરસ્પર લંબ એકમ સદિશો `hat i, hatj` અને `hatk ` માટે જમણા હાથની પદ્ધતિના સંદર્ભમાં જો `vec alpha =3hati-hatj, vecbeta = 2hati + hat j -3hatk` હોય તો `vec beta` ને સ્વરૂપે દર્શાવો, `vecbeta=vecbeta_1+vecbeta_2 ` જ્યાં `vecbeta_1` એ `vec alpha` ને સમાંતર છે અને `vecbeta_2` એ `vec alpha` ને લંબ છે.
View Solution
Example questions and complete solutions for chapter સદિશ બીજગણિત of NCERT Maths(Gujarati) of Class 12