Complete Solutions to Exercise of chapter સદિશ બીજગણિત of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | સદિશ બીજગણિત |
| NCERT | Exercise |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
ઉત્તરથી પૂર્વ તરફ `30^circ` ના ખૂણે 40 કિમીનું સ્થાનાંતર આલેખ દ્વારા દર્શાવો.
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 10 કિગ્રા
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 2 મી ઉત્તર-પશ્ચિમ દિશામાં
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : `40^circ`
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : 40 વૉટ
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : `10^(-19)` કુલંબ
View Solutionનીચે આપેલ માપને અદિશ અને સદિશમાં વર્ગીકૃત કરો : `20` મી/સે^(2)`
View Solutionનીચે આપેલ રાશિને અદિશ અને સદિશ રાશિઓમાં વર્ગીકૃત કરો : સમયગાળો
View Solutionનીચે આપેલ રાશિને અદિશ અને સદિશ રાશિઓમાં વર્ગીકૃત કરો : અંતર
View Solutionનીચે આપેલ રાશિને અદિશ અને સદિશ રાશિઓમાં વર્ગીકૃત કરો : બળ
View Solutionનીચે આપેલ રાશિને અદિશ અને સદિશ રાશિઓમાં વર્ગીકૃત કરો : વેગ
View Solutionનીચે આપેલ રાશિને અદિશ અને સદિશ રાશિઓમાં વર્ગીકૃત કરો : થયેલ કાર્ય
View Solutionઆકૃતિ 10.6 માં (એક ચોરસ), નીચે આપેલ સદિશો ઓળખો : સમઉદ્ભવ .

View Solutionઆકૃતિ 10.6 માં (એક ચોરસ), નીચે આપેલ સદિશો ઓળખો : સમાન .

View Solutionઆકૃતિ 10.6 માં (એક ચોરસ), નીચે આપેલ સદિશો ઓળખો : સમરેખ પરંતુ સમાન નહિ.

View Solutionનીચે આપેલા સદિશોનાં માનની ગણતરી કરો : `vec a = hat i + hat j + hat k` , `vec b = 2 hat i- 7 hat j - 3 hat k` , `vec c = 1/sqrt3 hat i +1/sqrt3 hat j - 1/sqrt3 hat k`
View Solutionસાબિત કરો કે સદિશ `hat i +hat j + hat k` એ અક્ષો OX, OY અને OZ સાથે સમાન ખૂણા બનાવે છે.
View Solutionનીયેના આપેલા 1 થી 8 સુધીના પ્રશ્ર્નોની ગણતરી કરી ટૂંકમાં જવાખ આપો (દરેક પ્રશ્ર્નના 2 ગુણ છે. )
ખિદુ R એ ખિધુઓ P અને Q ને જોડતા રેખાખંડનુ `2:1` ગુણોત્તરમાં (i) અંત: (ii) ખહિર્વિભાજન કરે છે. P અને Q ના સ્થાનસદિશો અનુક્રમે `\hat i+2\hat j-\hat k` અને `-\hat i+\hat j + \hat k` છે , તો ખિદુ R નો સ્થાનસદિશ શોધો.
View Solutionસાબિત કરો કે બિંદુઓ A, B અને C ના સ્થાનસદિશો અનુક્રમે `vec a = 3 hat i - 4 hat j – 4 hat k` , `vec b = 2 hat i - hat j + hat k`અને `vec c = hat i - 3 hat j - 5 hat k` હોય, તો તે કાટકોણ ત્રિકોણ રચે છે.
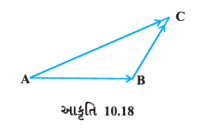
View Solutionત્રિકોણ ABC (આકૃતિ 10.18) માટે નીચેનામાંથી કયાં વિધાનો સત્ય નથી ?
View Solutionદર્શાવો કે નીચે આપેલ ત્રણ સદિશો પૈકી પ્રત્યેક સદિશ એકમ સદિશ છે : `1/7 (2 hat i+ 3 hat j + 6 hat k)`, `1/7 (3 hat i - 6 hat j+ 2 hat k)`, `1/7(6 hat i + 2 hat j -3 hat k)` વળી, સાબિત કરો કે આ સદિશો પરસ્પર લંબ છે.
View Solutionકોઈ પણ બે શૂન્યતર સદિશો `vec a` અને`vec b` માટે દર્શાવો કે `|vec a| vec b + |vec b| vec a` એ `|vec a| vec b - |vec b| vec a` ને લંબ છે.
View Solutionજો સદિશ `vec a = vec 0` અથવા `vec b = vec 0` હોય તો `vec a*vec b = 0`, પરંતુ પ્રતીપ, સત્ય હોય તે જરૂરી નથી. તમારા જવાબનું ઉદાહરણ સહિત સમર્થન કરો.
View Solutionનીયેના આપેલા 1 થી 8 સુધીના પ્રશ્ર્નોની ગણતરી કરી ટૂંકમાં જવાખ આપો (દરેક પ્રશ્ર્નના 2 ગુણ છે. )
જો ત્રિકોણ ABCના શિરોખિદુઓ A, B, C અનુક્રમે (1, 2, 3), (-1, 0, 0), (0, 1, 2) હોય, તો `angle ABC` શોધો. (`angle ABC` એ `vec(BA)` તથા `vec(BC)` વય્યેનો ખૂણે છે.)
View Solutionસાબિત કરો કે સદિશો `2 hat i - hat j + hat k`, `hat i -3 hat j -5 hat k` અને `3 hat i -4 hat j - 4 hat k`કાટકોણ ત્રિકોણનાં શિરોબિંદુઓ છે.
View Solutionનીયેના બહુવિકલ્પ પ્રશ્નોના જવાબ માટે સાયો વિકલ્પ પસંદ કરો .
જો `vec a` શૂન્યતર સદિશ હોય અને તેનું માન 'a' હોય અને `lamda` શૂન્યત્તર સદિશ હોય, તો `lamda` ની કઈ કિંમત માટે `lamda vec a` એકમ સદિશ થાય.
View Solutionજો `vec a = 0` અથવા `vec b = 0` ,તો `vec a xx vec b =0` શું પ્રતીપ સત્ય છે ? ઉદાહરણ દ્વારા તમારા જવાબનું સમર્થન કરો.
View Solutionનીચે આપેલા થી સુધીના પ્રશ્ર્નોની ગણતરી કરી ટૂંકમાં જવાબ આપો.
જો સમાંતરબાજુ ચતુષ્કોણની પાસેની બાજુઓ સદિશો ` vec a = vec i - vec j+3vec k` અને `vec b= 2 vec i- 7 vec j+ vec k` હોય, તો તેનું ક્ષેત્રફળ શોધો.
View Solutionનીયેના બહુવિકલ્પ પ્રશ્નોના જવાબ માટે સાયો વિકલ્પ પસંદ કરો
ધારો કે સદિશો `vec a` અને `vec b` આપેલા છે. `|vec a|=3` અને `|vec b|=\sqrt{2}/3` છે. જો `vec a times vec b` એકમ સદિશ હોય તો અને વચ્ચેનો ખૂણો ........હોય.
View Solutionલંબચોરસનાં શિરોબિંદુઓ A, B, C, D ના સ્થાનસદિશો અનુક્રમે `- hat i + 1/2 hat j+ 4 hat k`, `-hat i + 1/2 hat j+ 4 hat k`, `hat i - 1/2 hat j+ 4 hat k` અને `- hat i - 1/2 hat j+ 4 hat k` હોય, તો તે લંબચોરસનું ક્ષેત્રફળ
View Solutionસાબિત કરો કે સદિશ `vec a = hat i -2 hat j + 3 hat k`, `vec b = -2 hat i +3 hat j -4hat k` અને `vec c = hat i -3 hat j +5hat k` સમતલીય છે.
View Solutionસદિશ `vec a = hat i+ hat j+ hat k`, `vec b = hat i` અને `vec c =c_1 hat i+ c_2 hat j+ c_3 hat k` છે. (a) જો `c_1 = 1` અને `c_2 = 2` હોય, તો `vec a`, `vec b` અને `vec c` સમતલીય બને તે માટે `c_3` શોધો.
View Solutionસદિશ `vec a = hat i+ hat j+ hat k`, `vec b = hat i` અને `vec c =c_1 hat i+ c_2 hat j+ c_3 hat k` છે. (b) જો `c_2 = -1` અને `c_3 =1` હોય, તો સાબિત કરો કે `c_1` ની કોઈ પણ કિંમત માટે `vec a`, `vec b` અને `vec c` સમતલીય નથી.
View Solutionસાબિત કરો કે `4 hat i + 8 hat j+ 12 hat k`, `2 hat i+ 4 hat j + 6 hat k` , `3 hat i +5 hat j+ 4 hat k`અને `5 hat i + 8 hat j + 5 hat k` સ્થાનસદિશ ધરાવતાં ચાર બિંદુઓ સમતલીય છે.
View Solutionનીયે આપેલા 1 થી 8 સુધીના પ્રશ્ર્નોની ગણતરી કરી ટૂંકમાં જવાખ આપો (દરેક પ્રશ્ર્નના 2 ગુણ છે. )
જો`vec a+ vec b, vec b+ vec c` અને `vec c +vec a` સમતલીય હોય, તો સાબિત કરો કે `vec a, vec b` અને `vec c` સમતસીય છે.
View Solutionએક છોકરી પશ્ચિમ દિશામાં 4 કિમી ચાલે છે. પછી તે ઉત્તરથી પૂર્વ તરફ `30^circ` ના ખૂણે 3 કિમી ચાલે છે અને થોભે છે. મુસાફરીમાં પ્રારંભ બિંદુથી છોકરીનું સ્થળાંતર શોધો.
View Solutionજો `vec a = vec b+ vec c` તો શું `|vec a| = |vec b| +|vec c|` સત્ય છે? તમારા જવાબનું સમર્થન કરો.
View Solutionx ના જે મૂલ્ય માટે `x (hat i + hat j + hat k)` એકમ સદિશ હોય તે મૂલ્ય શોધો.
View Solutionજે સદિશનું માન 5 એકમ હોય અને સદિશો `vec a = 2 hat i+ 3 hat j - hat k` અને `vec b = hat i - 2 hat j + hat k` ના પરિણામી સદિશને સમાંતર હોય તે સદિશ શોધો.
View Solutionજો `vec a = hat i+ hat j+ hat k`, `vec b = 2 hat i - hat j + 3 hat k` અને `vec c = hat i - 2 hat j+ hat k` હોય, તો સદિશ `2 vec a - vec b + 3 vec c` ને સમાંતર એકમ સદિશ શોધો.
View Solutionબિંદુઓ P અને Q ના સ્થાન દિશો `(2 vec a + vec b)` અને `(vec a -3 vec b)` છે. જો બિંદુ R એ P અને Q ને જોડતા રેખાખંડનું 1: 2 ગુણોત્તરમાં બહિવિભાજન કરે, તો બિંદુ R નો સ્થાનસદિશ શોધો. વળી, સાબિત કરો કે P એ રેખાખંડ RQ નું મધ્યબિંદુ છે.
View Solutionસમાંતરબાજુ ચતુષ્કોણની પાસપાસેની બે બાજુઓ `2 hat i - 4 hat j + 5 hat k` અને `hat i - 2 hat j- 3 hat k` છે. તેના વિકર્ણને સમાંતર એકમ સદિશ શોધો. વળી, તેનું ક્ષેત્રફળ શોધો.
View Solutionસાબિત કરો કે જે સદિશ અક્ષો OX, OY અને OZ સાથે સમાન માપવાળા ખૂણા આંતરતો હોય તેના દિક્કોસાઇન `1/sqrt3, 1/sqrt3, 1/sqrt3` છે.
View Solutionધારો કે `vec a = hat i+ 4 hat j+ 2 hat k`, `vec b = 3 hat i - 2 hat j+ 7 hat k` અને `vec c = 2 hat i - hat j+ 4 hat k` છે. સદિશો `vec a` અને `vec b` ને લંબ હોય તથા `vec c*vec d = 15` થાય તેવો સદિશ `vec d` શોધો.
View Solutionજે એકમ સદિશની દિશા સદિશો `2 hat i+ 4 hat j - 5 hat k` અને `lambda hat i +2 hat j+ 3hat k`ના સરવાળાની દિશામાં હોય તે સદિશનો `hat i+ hat j + hat k` સાથે અદિશ ગુણાકાર 1 હોય, તો `lambda` શોધો.
View Solutionઆપેલ `vec a ne vec 0`, `vec b ne vec 0` માટે સાબિત કરો : જો `(vec a +vec b)*(vec a+ vec b) =|vec a|^(2) + |vec b|^(2)` તો અને તો જ `vec a`અને `vec b` પરસ્પર લંબ છે.
View Solution`hat i*(hat jxxhat k) +hat j*(hat ixxhat k) + hat k*(hat ixxhat j)` નું મૂલ્ય.........
View Solutionજો `theta` એ કોઈ પણ બે સદિશો `vec x` અને `vec y` વચ્ચેનો ખૂણો હોય, તો `theta` = ........... માટે `|vec x*vec y| = |vec x xx vec y|` .
View Solution
Exercise questions and complete solutions for chapter સદિશ બીજગણિત of NCERT Maths(Gujarati) of Class 12