Complete Solutions to Exercise of chapter વિદ્યુતભારો અને ક્ષેત્રો of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | વિદ્યુતભારો અને ક્ષેત્રો |
| NCERT | Exercise |
| Number Of Questions | 46 |
| Academic Year | 2023-24 |
`2 xx 10^(-7) C` અને `3 xx 10^(-7) C` વિદ્યુતભાર ધરાવતા અને એકબીજાથી હવામાં 30 cm અંતરે રહેલા બે વિદ્યુતભારિત ગોળાઓ વચ્ચે કેટલું બળ લાગે?
View Solutionહવામાં રાખેલા `0.4mu C` જેટલા વિદ્યુતભારો ધરાવતા એક ખૂબ નાના ગોળા પર, `-0.8 muC` જેટલો વિદ્યુતભાર ધરાવતા બીજા ખૂબ નાના ગોળા દ્વારા લગાડવામાં આવતું કુલંબીય બળ `0.2 N` હોય તો આ બે ગોળાઓ વચ્ચેનું અંતર શોધો.
View Solutionહવામાં રાખેલા `0.4mu C` જેટલા વિદ્યુતભારો ધરાવતા એક ખૂબ નાના ગોળા પર, `-0.8 muC` જેટલો વિદ્યુતભાર ધરાવતા બીજા ખૂબ નાના ગોળા દ્વારા લગાડવામાં આવતું કુલંબીય બળ `0.2 N` હોય તો પહેલાં ગોળા વડે બીજા ગોળા પર લગાડવામાં આવતું કુલંબીય બળ કેટલું હશે ?
View Solutionદર્શાવો કે, ગુણોત્તર `ke^2/(Gm_e m_p`) એ પરિમાણરહિત છે. આ ગુણોત્તરનું મૂલ્ય શોધો. તે શું દર્શાવે છે ?
View Solutionકોઈપણ પદાર્થે ધારણ કરેલો વિદ્યુતભાર કવોન્ટમીકૃત હોય છે.(એટલે કે કવોન્ટમીકરણ પામેલો હોય છે.) આ વાક્યનો અર્થ જણાવો.
View Solutionસ્થળ એટલે કે મોટા માપક્રમ પર વિદ્યુતભારો સાથે કામ કરતી વખતે આપણે વિદ્યુતભારનું ક્વૉન્ટમીકરણ શા માટે અવગણી શકીએ છીએ?
View Solution"જયારે કાચના સળિયાને રેશમી કાપડ સાથે ઘસવામાં આવે છે ત્યારે તે બંને વિદ્યુતભારિત થાય છે." આવા ઉદાહરણોમાં વિદ્યુતભારનું સંરક્ષણ કેવી રીતે થાય છે, તે સમજાવો.
View Solution`10 cm` જેટલી બાજુની લંબાઈ ધરાવતા ચોરસ `ABCD` નાં શિરોબીંદુઓ પર અનુક્રમે `+2 muC`, `-5 muC`, `+2 muC` અને `-5 muC` જેટલા બિંદુવત વિદ્યુતભારો આવેલાં છે. તો આ તંત્ર વડે, ચોરસના મધ્યકેન્દ્ર પર મૂકેલા `+1muC` જેટલા બિંદુવત વિદ્યુતભાર પરનું પરિણામી કુલંબીય બળ શોધો.
View Solutionસ્થિત વિદ્યુત ક્ષેત્ર રેખા એ સળંગ વક્ર છે. એટલે કે ક્ષેત્ર રેખાને અચાનક ભંગાણો (ગાબડાં, વિચ્છેદ) ન હોઈ શકે. આવું શા માટે?
View Solutionબે વિદ્યુતક્ષેત્ર રેખાઓ શા માટે એકબીજાને છેદી શકતી નથી ?
View Solutionબે બિંદુવત વિદ્યુતભારો `q_A = 3 muC` અને `q_B = -3 muC` શૂન્યવકાશમાં એકબીજાથી `20 cm` અંતરે આવેલા છે. આ બે વિદ્યુતભારોને જોડતા રેખાખંડ `bar AB` નાં મધ્યબિન્દુ આગળ વિદ્યુતક્ષેત્ર શોધો.
View Solutionબે બિંદુવત્ વિદ્યુતભારો `q_(A) = 3 mu C` અને `qB = -3 mu C` એકબીજાથી શૂન્યાવકાશમાં `20 cm` દૂર રહેલા છે.
(a) બે વિદ્યુતભારોને જોડતી રેખાના મધ્યબિંદુ O આગળ વિદ્યુતક્ષેત્ર કેટલું હશે?
(b) જો `1.5 times 10^(-9) C` માન ધરાવતો એક ઋણ પરિક્ષણ વિદ્યુતભાર આ બિંદુએ મૂકવામાં આવે, તો તેના પર લાગતું બળ કેટલું હશે?
View Solutionએક તંત્રમાં બે બિંદુવત વિદ્યુતભારો `q_A = 2.5 xx 10^-7 C` અને `q_B =-2.5 xx 10^-7 C` અનુક્રમે બિંદુ A (0,0, -15) cm અને B = (0, 0, +15) cm આગળ આવેલા છે. તો આ તંત્રનો કુલ વિદ્યુતભાર તથા વિદ્યુત ડાઈપોલ મોમેન્ટ શોધો.
View Solution`5 xx 10^4 NC^-1` જેટલા સમાન વિદ્યુતક્ષેત્રમાં ક્ષેત્ર સાથે `30^circ` ના ખૂણે મુકેલી `4 xx 10^-9 cm` જેટલી ડાઈપોલ મોમેન્ટવાળી વિદ્યુતીય ડાઈપોલ પર લગાડવામાં આવતું ટોર્ક શોધો.
View Solutionઊન સાથે ઘસેલા એક પોલીથીન ટુકડા પર `3 **10^(-7) C` ઋણ વિદ્યુતભાર છે. સ્થાનાંતરિત થયેલા ઇલેક્ટ્રૉનની સંખ્યા શોધો. તેઓ શાના પરથી શાના પર સ્થાનાંતરિત થયા છે ?
View Solutionપોલીથીનના એક ટુકડાને ઊન (wool) સાથે ઘસતા આ ટુકડો `3 xx 10^-7 C` નો ઋણ વિદ્યુતભાર પ્રાપ્ત કરે છે. શું અત્રે ઊનથી પોલીથીન તરફ દળનો વિનિમય થયો હશે ?
View Solutionતાંબાના વિદ્યુતભારિત કરેલા બે ખૂબ નાના ગોળાઓ A અને B ના કેન્દ્રો વચ્ચેનું અંતર `50 cm` છે. દરેક ગોળો `6.5 xx 10^-7 C` જેટલો વિદ્યુતભાર ધરાવે છે. તેમની વચ્ચેનું પારસ્પરિક અપાકર્ષી કુલંબીય બળ શોધો.
View Solutionતાંબાના વિદ્યુતભારિત કરેલા બે ખૂબ નાના ગોળાઓ A અને B ના કેન્દ્રો વચ્ચેનું અંતર `50 cm` છે. દરેક ગોળો `6.5 xx 10^-7 C` જેટલો વિદ્યુતભાર ધરાવે છે. જો તેમની પરના વિદ્યુતભારનું મૂલ્ય બમણું કરવામાં આવે અને તેમની વચ્ચેનું અંતર અડધું કરવામાં આવે તો તેમની વચ્ચેનું નવું કુલંબીય બળ કેટલું બનશે ?
View Solutionઉપરોક્ત દાખલામાં A અને B ગોળાઓની ત્રિજ્યાઓ સમાન હોય તથા એટલી જ સાઈઝના ગોળા C ને પહેલા A સાથે સંપર્કમાં લાવી A થી છૂટો પાડ્યા બાદ B સાથે સંપર્કમાં લાવીને B થી છૂટો પાડવામાં આવે છે. હવે, A અને B ને પ્રારંભિક અંતરે રાખતા તેમની વચ્ચેનું નવું કુલંબીય બળ કેટલું બનશે ?
View Solutionઆકૃતિમાં સમાન વિદ્યુતક્ષેત્રમાંથી પસાર થતા ત્રણ વિદ્યુતભારિત કણોના ગતિમાંર્ગે દર્શાવેલ છે.તેમના પરના વિદ્યુતભારોના ચિન્હ નક્કી કરો. તેમાંથી ક્યા કણ માટે વિદ્યુતભાર અને દળનો ગુણોત્તર સૌથી મોટો છે ?

View Solutionએકસમાન વિદ્યુતક્ષેત્ર `E = 3 times 10^(3) N//C` નો વિચાર કરો.
(a) `yz` સમતલને સમાંતરે જેનું સમતલ હોય તેવા `10 cm` ની બાજુવાળા ચોરસમાંથી આ ક્ષેત્રનું ફ્લક્સ કેટલું હશે? (b) જો વિદ્યુતક્ષેત્ર જ ચોરસના સમતલને દોરેલો લંબ `x-અક્ષ` સાથે `60^(@)` નો કોણ બનાવે તો તેમાંથી ફ્લક્સ કેટલું હશે?
View Solution`E = 3 XX 10^3i^^N/C` જેટલા સમાન વિદ્યુતક્ષેત્રમાં જયારે આ ચોરસને દોરેલો લંબ, X અક્ષ સાથે `60^circ` નો ખૂણો બનાવે ત્યારે આ ચોરસમાંથી પસાર થતું વિદ્યુતીય ફ્લક્સ શોધો.
View Solution20 cmની બાજુવાળા એક ઘન કે જેની બાજુઓ યામ સમતલોને સમાંતર રાખેલ હોય તેમાંથી સ્વાધ્યાય 1.15માં દર્શાવેલ વિદ્યુતક્ષેત્રનું ફલક્સ કેટલું હશે?
View Solutionએક બંધ બોક્સમાંથી `8 xx 10^3 Nm^2/C` જેટલું ચોખ્ખું વિદ્યુતીય ફ્લક્સ બહાર આવે છે. આ બોક્સ વડે ઘેરાતો ચોખ્ખો વિદ્યુતભાર શોધો.
View Solutionએક બંધ બોક્સમાંથી `8 xx 10^3 Nm^2/C` જેટલું ચોખ્ખું વિદ્યુતીય ફ્લક્સ બહાર આવે છે. જો આ બોક્સ સાથે સંકળાતું ચોખ્ખું વિદ્યુતીય ફ્લક્સ શૂન્ય હોત તો શું આવું કહી શકાય કે આ બોકસમાં કોઈ જ વિદ્યુતભાર નથી ? તમારા જવાબ માટે કારણ આપો.
View Solutionઆકૃતિ 1.34માં દર્શાવ્યા મુજબ 10 cm બાજુવાળા એક ચોરસના કેન્દ્રથી બરાબર ઉપર 5 cm અંતરે `+10 muC` બિંદુવતું વિદ્યુતભાર રહેલો છે. ચોરસમાંથી વિદ્યુત ફલક્સનું મૂલ્ય કેટલું હશે ? (સૂચન : ચોરસને 10 cmની ધારવાળા ઘનની એક બાજુ તરીકે વિચારો.)
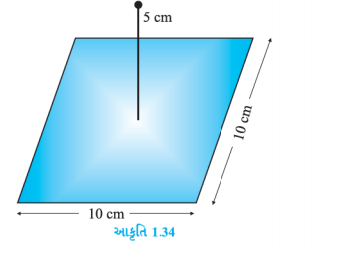
View Solutionકેન્દ્ર પર રહેલા એક બિંદુવત વિદ્યુતભારને કારણે તેને ઘેરી લેતા `10 cm` ત્રિજ્યાવાળા ગોળાકાર બંધ પૃષ્ઠ સાથે `-1 xx 10^3 Nm^2/C` જેટલું ચોખ્ખું વિદ્યુતીય ફ્લક્સ સંકળાય છે. જો આ પૃષ્ઠની ત્રિજ્યા બમણી કરવામાં આવે તો તેની સાથે સંકળાતું વિદ્યુતીય ફ્લક્સ કેટલું બનશે ?
View Solutionકેન્દ્ર પર રહેલા એક બિંદુવત વિદ્યુતભારને કારણે તેને ઘેરી લેતા `10 cm` ત્રિજ્યાવાળા ગોળાકાર બંધ પૃષ્ઠ સાથે `-1 xx 10^3 Nm^2/C` જેટલું ચોખ્ખું વિદ્યુતીય ફ્લક્સ સંકળાય છે. ઘેરાતો વિદ્યુતભાર શોધો.
View Solution`10 cm` ત્રિજ્યાવાળા વાહક ગોળાના કેન્દ્રથી `20 cm` અંતરે `1.5 xx 10^3 N/C` જેટલું વિદ્યુતક્ષેત્ર ત્રિજ્યાવર્તી રીતે અંદરની તરફ મળે છે. તો આ ગોળાની સપાટી પરનો વિદ્યુતભાર શોધો.
View Solution`2.4 m`નો વ્યાસ ધરાવતા એક સમાન વિદ્યુતભારિત ગોળા પર વિદ્યુતભારની પૃષ્ઠ ઘનતા `80.0 mu C//m^(2)` છે.
(a) ગોળા પરનો વિદ્યુતભાર શોધો.
(b) ગોળાની સપાટીમાંથી બહાર જતું કુલવિદ્યુત ફલક્સ કેટલું હશે?
View Solution`2.4 m`નો વ્યાસ ધરાવતા એક સમાન વિદ્યુતભારિત ગોળા પર વિદ્યુતભારની પૃષ્ઠ ઘનતા `80.0 mu C//m^(2)` છે.
(a) ગોળા પરનો વિદ્યુતભાર શોધો.
(b) ગોળાની સપાટીમાંથી બહાર જતું કુલવિદ્યુત ફલક્સ કેટલું હશે?
View Solutionવિદ્યુતભારનું નિયમિત વિતરણ ધરાવતી અનંત લંબાઈવાળી વિદ્યુતભાર રેખાથી `2 cm` જેટલા લંબ અંતરે ઉદભવતું વિદ્યુતક્ષેત્ર `9 xx 10^4 N/C` હોય તો તેના માટે વિદ્યુતભારની રેખીય ઘનતા શોધો.
View Solutionબે મોટી, પાતળી ધાતુની પ્લેટો એકબીજાની નજીક અને સમાંતર છે. તેમની અંદરની બાજુઓ પર વિરૂદ્ધ ચિહ્નો ધરાવતી અને `17.0 xx 10^(-22)C/m^(2)` મૂલ્યની વિદ્યુતભારની પૃષ્ઠ ઘનતા છે. બંને પ્લેટોની વચ્ચેના વિસ્તારમાં, વિદ્યુતક્ષેત્ર E શોધો.
View Solutionમિલિકનના ઑઇલ ડ્રોપ પ્રયોગમાં 12 વધારાના ઇલેક્ટ્રૉન ધરાવતું એક ઑઇલ ડ્રોપ `2.55 ** 10^(4)N C^(-1)` ના સમાન વિધુતક્ષેત્રની અસર હેઠળ સ્થિર રાખવામાં આવ્યું છે. જો ઑઇલની ઘનતા `1.26 g cm^(-3)` હોય તો તે દ્રોપની ત્રિજ્યા શોધો. (`g = 9.81 ms^(-2)`, `e=1.60 **10^(-19) c`
View Solutionઆકૃતિ 1.35માં દર્શાવેલ વક્રો પૈકી કયો/કયા વક્ર સ્થિતવિદ્યુત ક્ષેત્ર રેખાઓ રજૂ કરી શકશે નહિ ?
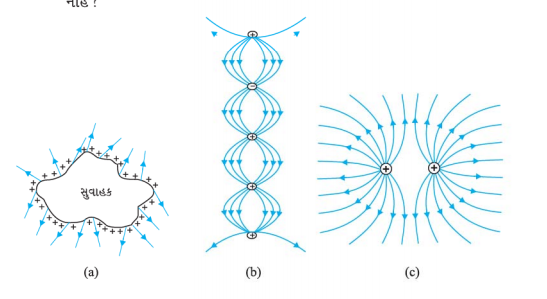
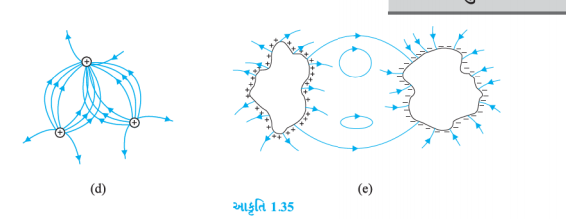
View Solutionએક વિસ્તારમાં વિદ્યુતક્ષેત્ર માત્ર Z અક્ષ પર અસ્તિત્વ ધરાવે છે. જેમાં `+Z` દિશામાં વિદ્યુતક્ષેત્રનું મૂલ્ય `10^5 NC^-1m^-1` નાં દરથી વધી રહ્યું છે. તેમાં `-Z` દિશામાં `10^-7 cm` જેટલી ડાઈપોલ મોમેન્ટ ધરાવતી વિદ્યુતીય ડાઈપોલને મૂકતા તેના પર લાગતાં પરિણામી વિદ્યુતીય બળ અને ટોર્ક શોધો.
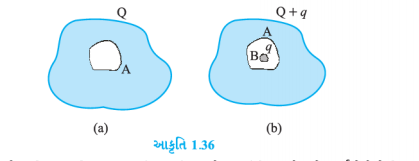
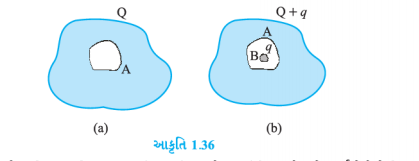
View Solutionઆકૃતિ 1.36(a)માં દર્શાવ્યા મુજબ એક બખોલ (Cavity) ધરાવતા સુવાહક મને Q વિદ્યુતભાર આપેલ છે. દર્શાવો કે સમગ્ર વિદ્યુતભાર સુવાહકની બહારની સપાટી પર જ દશ્યમાન થશે.
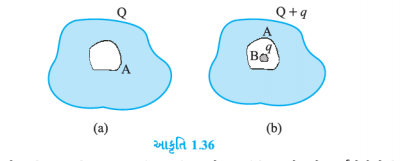
View Solutionq વિદ્યુતભાર ધરાવતો બીજો સુવાહક, કેવીટી (બખોલ)ની અંદર Aથી અલગ રહે તેમ દાખલ કરેલ છે. દર્શાવો કે Aની બહારની સપાટી પરનો કુલ વિદ્યુતભાર Q+q (આકૃતિ 1.36(b)) છે.
View Solutionએક સંવેદી ઉપકરણને તેના પરિસરમાંના (આસપાસના) પ્રબળ સ્થિતવિદ્યુત ક્ષેત્રોથી બચાવવું (Shield કરવું) છે. આ માટે એક શક્ય ઉપાય સૂચવો.
View Solutionએક પોલા વિદ્યુતભારિત સુવાહકની સપાટી પર એક નાનું છિદ્ર કાપેલ છે. દર્શાવો કે તે છિદ્રમાં વિદ્યુતક્ષેત્ર `(sigma/2 epsilon_0) n^(^)` છે. જ્યાં, `n^(^)`બિહાર તરફની લંબ દિશામાંનો એકમ સદિશ છે અને `sigma` છિદ્રની નજીક વિદ્યુતભારની પૃષ્ઠઘનતા છે.
View Solutionગૉસના નિયમનો ઉપયોગ કર્યા સિવાય વિદ્યુતભારની સમાન રેખીય ઘનતા `lambda` ધરાવતા લાંબા પાતળા તારને લીધે ઉદ્ભવતા વિદ્યુતક્ષેત્રનું સૂત્ર મેળવો. (સૂચન : કુલંબના નિયમનો સીધો ઉપયોગ કરો અને જરૂરી સંકલનની ગણતરી કરો.)
View Solutionહવે એવું માનવામાં આવે છે કે પ્રોટોન અને ન્યૂટ્રોન (જે સામાન્ય દ્રવ્યના ન્યુક્લિયસોની રચના કરે છે.) પોતે પણ કુવાસ તરીકે ઓળખાતા વધારે પ્રાથમિક એકમોના બનેલા છે. એક પ્રોટોન અને એક ન્યૂટ્રોન દરેક, ત્રણ કવાર્ટ્સના બનેલા છે. (u વડે દર્શાવાતા) કહેવાતા up ક્લાર્ક જેનો વિદ્યુતભાર +(2/3)e છે અને (d વડે દર્શાવાતા) કહેવાતા down ક્લાર્ક જેનો વિદ્યુતભાર (-1/3)e છે અને ઇલેક્ટ્રોન એ બધા ભેગાં મળીને સામાન્ય દ્રવ્ય બનાવે છે. બીજા પ્રકારના ક્લાર્ક પણ શોધાયા છે જેઓ દ્રવ્યના વિવિધ અસામાન્ય પ્રકાર ઉપજાવે છે.) પ્રોટોન અને ન્યૂટ્રોન માટે શક્ય ક્લાર્ક બંધારણનું સૂચન કરો.
View Solutionયાદ્ચ્છિક રીતે (મનપસંદ રીતે ) કોઈ સ્થિત વિદ્યુતક્ષેત્ર ધ્યાનમાં લો. તેમના તટસ્થબિંદુ (અથવા શિથિલ બિંદુ ) આગળ (એટલે કે જ્યાં પરિણામી વિદ્યુતક્ષેત્ર `vec E = vec 0` હોય) પરીક્ષણ વિદ્યુતભાર મૂકવામાં આવે તો તે સ્થાને તે અવશ્યપણે અસ્થાયી સમતોલન સ્થિતિમાં જ હોય છે. તેવું સાબિત કરો.
View Solutionઉપરોક્ત પરિણામની ચકાસણી, એકબીજાથી અમુક અંતરે રાખેલા, સમાન મૂલ્યના બે સજાતીય વિદ્યુતભારોની બનેલી સાદી સંરચના (ગોઠવણ) વડે કરો.
View Solutionm દળ અને (-q) વિદ્યુતભાર ધરાવતો એક કણ બે વિદ્યુતભારિત પ્લેટોની વચ્ચે `v_x` વેગથી પ્રારંભમાં x-અક્ષને સમાંતરે દાખલ થાય છે (આકૃતિ 1.33માં કણ-1ની જેમ). દરેક પ્લેટની લંબાઈ L છે અને પ્લેટો વચ્ચે સમાન વિદ્યુતક્ષેત્ર જાળવી રાખવામાં આવે છે. દર્શાવો કે પ્લેટના દૂરના છેડે કણનું શિરોલંબ વિચલન `qEL^(2)/2mv_x^(2)` છે. ધોરણ XI, ભૌતિકવિજ્ઞાન પાઠ્યપુસ્તકના પરિચ્છેદ 4.10માં ચર્સેલ પ્રક્ષિપ્ત પદાર્થની ગુરુત્વીય ક્ષેત્રમાંની ગતિ સાથે આ ગતિને સરખાવો.
View Solutionધારોકે સ્વાધ્યાય 1.33માંનો કણ છે, `v_x=2.0 ** 10^(6)m s^(-1)` વેગથી પ્રક્ષિપ્ત કરેલો ઇલેક્ટ્રૉન છે. 0.5 cmનું અંતર ધરાવતી પ્લેટો વચ્ચેનું E, જો `9.1 ** 10^(2) N/C` હોય તો ઇલેક્ટ્રૉન ઉપરની પ્લેટને ક્યાં અથડાશે? (`abx|e| =1.6 **10^(-19)C,` `m_e=9.1 **10^(-31)kg`)
View Solution
Exercise questions and complete solutions for chapter વિદ્યુતભારો અને ક્ષેત્રો of NCERT Physics(Gujarati) of Class 12