Complete Solutions to objective of chapter WORK, ENERGY AND POWER of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| NEET PREVIOUS YEAR | objective |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
Consider a drop of rain water having mass `1 gram` , 50 `m//s` Take `g` constant with a volume `10 m//s^(2)`. The work done by the
(i) gravitational force and the
(ii) resistive force of air is :
View SolutionA body of mass `1 kg` begins to move under the action of a time dependent force `vec F = (2 t hat I + 3 t^(2) hat j) N`, where `hat i` and `hat j` are unit vectors along x-and y-axes. What power will be developed by the force at the time `t` ?
View SolutionWhat is the minimum velocity with which a body of mass m must enter a vertical loop of radius `R` so that it can complete the loop?
View SolutionA paritcal of mass `10 g` moves along a circle of radius `6.4 cm` with a constant tangennitial acceleration. What is the magnitude of this acceleration . What is the magnitude of this acceleration if the kinetic energy of the partical becomes equal to `8 xx 10^(-4) J` by the end of the second revolution after the beginning of the motion?
View SolutionTwo identical balls `A and B` having velocity of `0.5 m//s and -0.3 m//s` respectively collide elastically in one dimension. The velocities of `B and A` after the collision respectively will be
View SolutionA partical moves from a point `(-2hati + 5hatj)` to `(4hati + 3hatj)` when a force of (4hati + 3hatj) N` is applied . How much work has been done by the force?
View SolutionTwo similar springs `P` and `Q` have spring constant `K_(P)` and `K_(Q)` such that `K_(P) gt K_(Q)`. They are stretched, first by the same amount (case a), then the same force (case b). The work done by the spring `W_(P)` and `W_(Q)` are related as, in case (b), respectively
View SolutionA block of mass 10 kg, moving in x-direction with a constant speed of `10ms^(-1)`, is subjected to a retarding force `F=0.1xxJ//m` during its travel from x=20 m to 30 m. Its final KE will be
View SolutionA partical of mass `m` is driven by a machine that deleveres a constant power `k` watts. If the partical starts from rest the force on the partical at time `t` is
View SolutionTwo particles of masses `m_(1),m_(2)` move with initial velocities `u_(1)` and `u_(2)`. On collision, one of the particles get excited to higher level, after absording enegry. If final velocities of particles be `v_(1)` and `v_(2)` then we must have
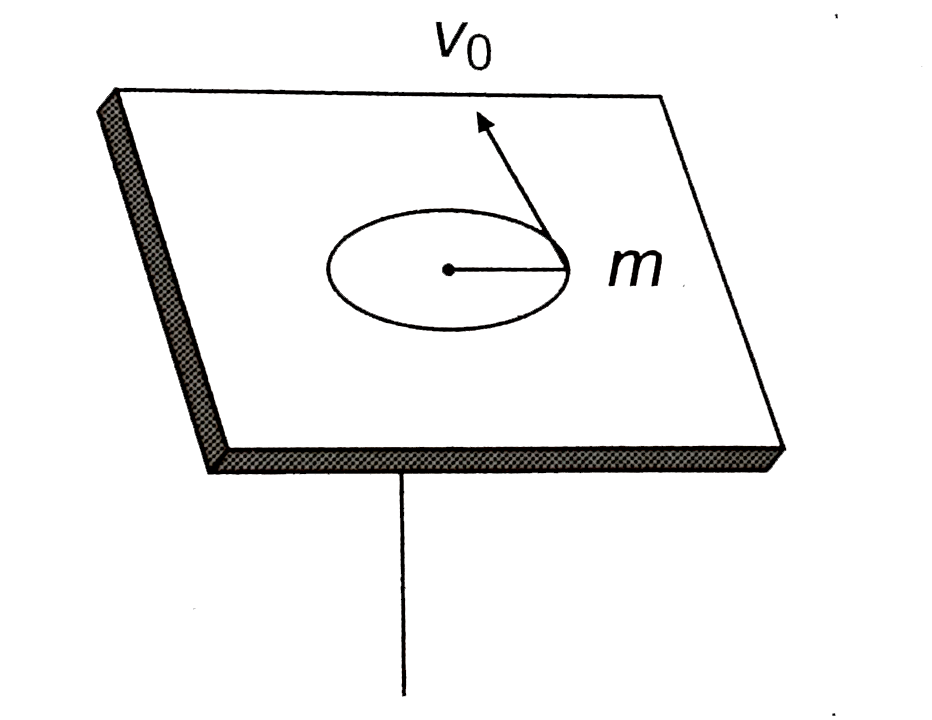
View SolutionA mass `m` moves in a circles on a smooth horizontal plane with velocity `v_(0)` at a radius `R_(0)`. The mass is atteched to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally `m` moves in a cricle of radius `(R_(0))/(2)`. the final value of the kinetic energy is
View SolutionA ball is thrown vertically downwards from a height of 20m with an intial velocity `v_(0)`. It collides with the ground, loses 50% of its energy in collision and rebounds to the same height. The intial velocity `v_(0)` is (Take, g =10 `ms^(-2)`)
View SolutionThe heart of a man pumps 5 liters of blood through the arteries per minute at a pressure of 150 mm of mercury. If the density of mercury be `13.6xx10^(3) kg//m^(3)` and `g=10 m//s^(2)` then the power of heat in watt is :
View SolutionOn a friction surface a block a mass `M` moving at speed `v` collides elastic with another block of same mass `M` which is initially at rest . After collision the first block moves at an angle `theta` to its initial direction and has a speed `(v)/(3)`. The second block's speed after the collision is
View SolutionA body of mass (4m) is laying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each mass (m) move perpedicular to each other with equal speeds (v). Total kinetic energy generated due to explosion is
View SolutionA uniform force of `(3hati+hatj)` N acts on a particle of mass 2kg. Hence, the particle is displaced from position `(2hati+hatk)`m to position `(4hati+3hatj-hatk)`m. The work done by the force on the particle is
View SolutionA body of mass `m` taken form the earth's surface to the height is equal to twice the radius `(R)` of the earth. The change in potential energy of body will be
View SolutionThe potential energy of a particle in a force field is:
`U = (A)/(r^(2)) - (B)/(r )`,. Where `A` and `B` are positive
constants and `r` is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View SolutionThe potential energy of a system increased if work is done
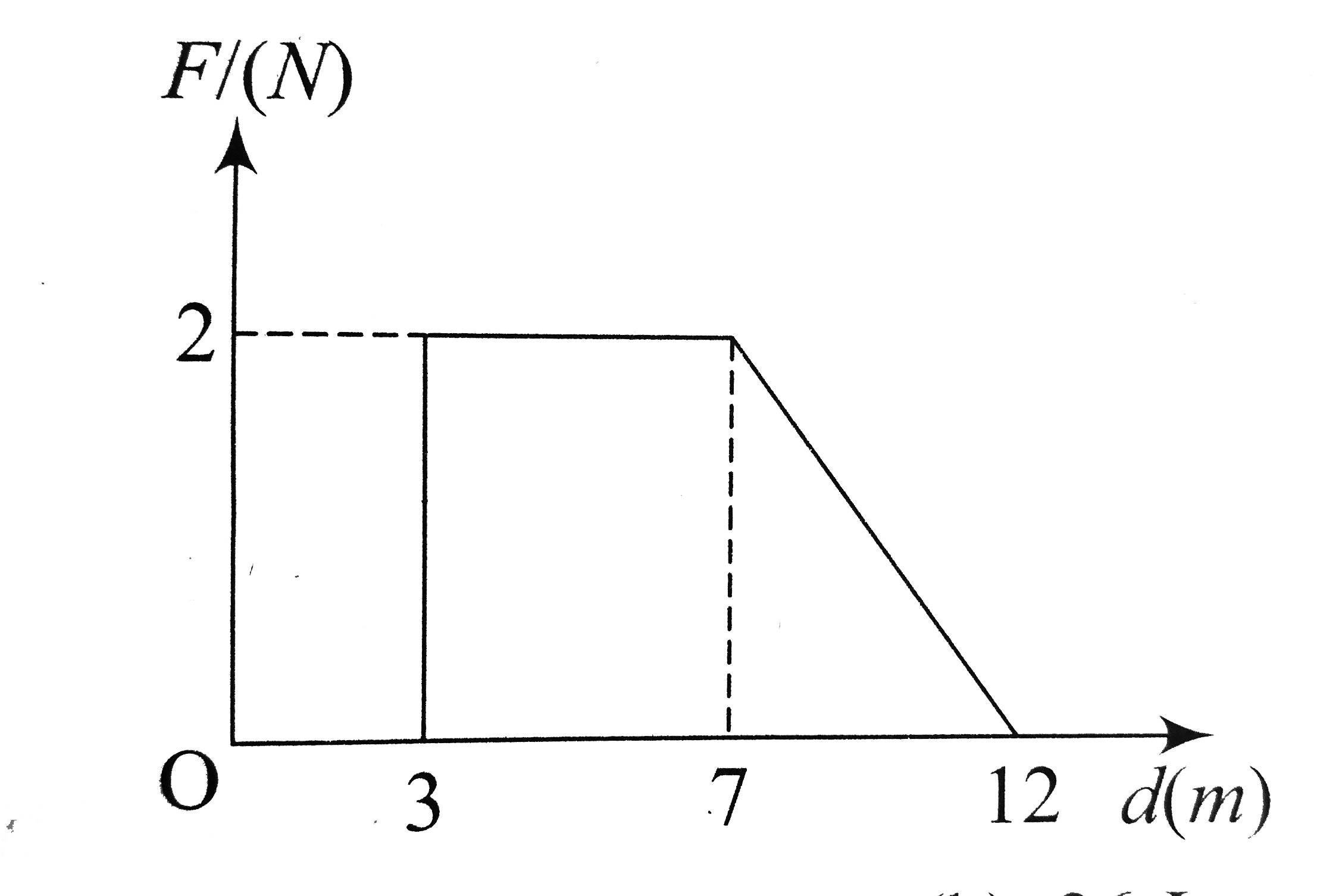
View Solutionforce `F` on a partical moving in a straight line veries with distance `d` as shown in the figure. The work done on the partical during its displacement of `12 m` is
View SolutionAn engine pumps water through a hose pipe. Water passes through the pipe and leaves it with a velocity of `2 ms^(-1)`. The mass per unit length of water in the pipe is `100 kgm^(-1)`. What is the power of the engine?
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionAn engine pumps water continously through a hose. Water leave the hose with a velocity `v` and `m` is the mass per unit length of the Water jet. What is the rate at Which kinetic energy is imparted to water?
View SolutionA body of mass `1 kg` is thrown upwards with a velocity `20 ms^(-1)`. It momentarily comes to rest after attaining a height of `18 m`. How much energy is lost due to air friction? `(g = 10 ms^(-2))`
View SolutionAn explosion blows a rock into three parts. Two parts go off at right angles to each other . These two are `1 kg` first part moving with a velocity of `12 ms^(-1) and 2 kg` second part moving with a velocity of `8 ms^(-1)`. If the third part flies off with a velocity of `4 ms^(-1)`. Its mass would be
View SolutionA shell of mass `200g` is ejected from a gun of mass `4 kg` by an explosion that generate `1.05 kJ` of energy. The initial velocity of the shell is
View SolutionWater falls from a height of `60 m` at the rate `15 kg//s` to operate a turbine. The losses due to frictional forces are `10%` of energy . How much power is generated to by the turbine? (`g=10 m//s^(2)`)
View Solution300J of work is done in slinding a 2 kg block up an inclined plane of height 10m. Taking g =`10m//s^(2)` , work done against friction is
View SolutionA body of mass `3 kg` is under a constant force which causes a displacement `s` metre in it, given by the relation `s=(1)/(3)t^(2)`, where `t` is in seconds. Work done by the force in 2 seconds is
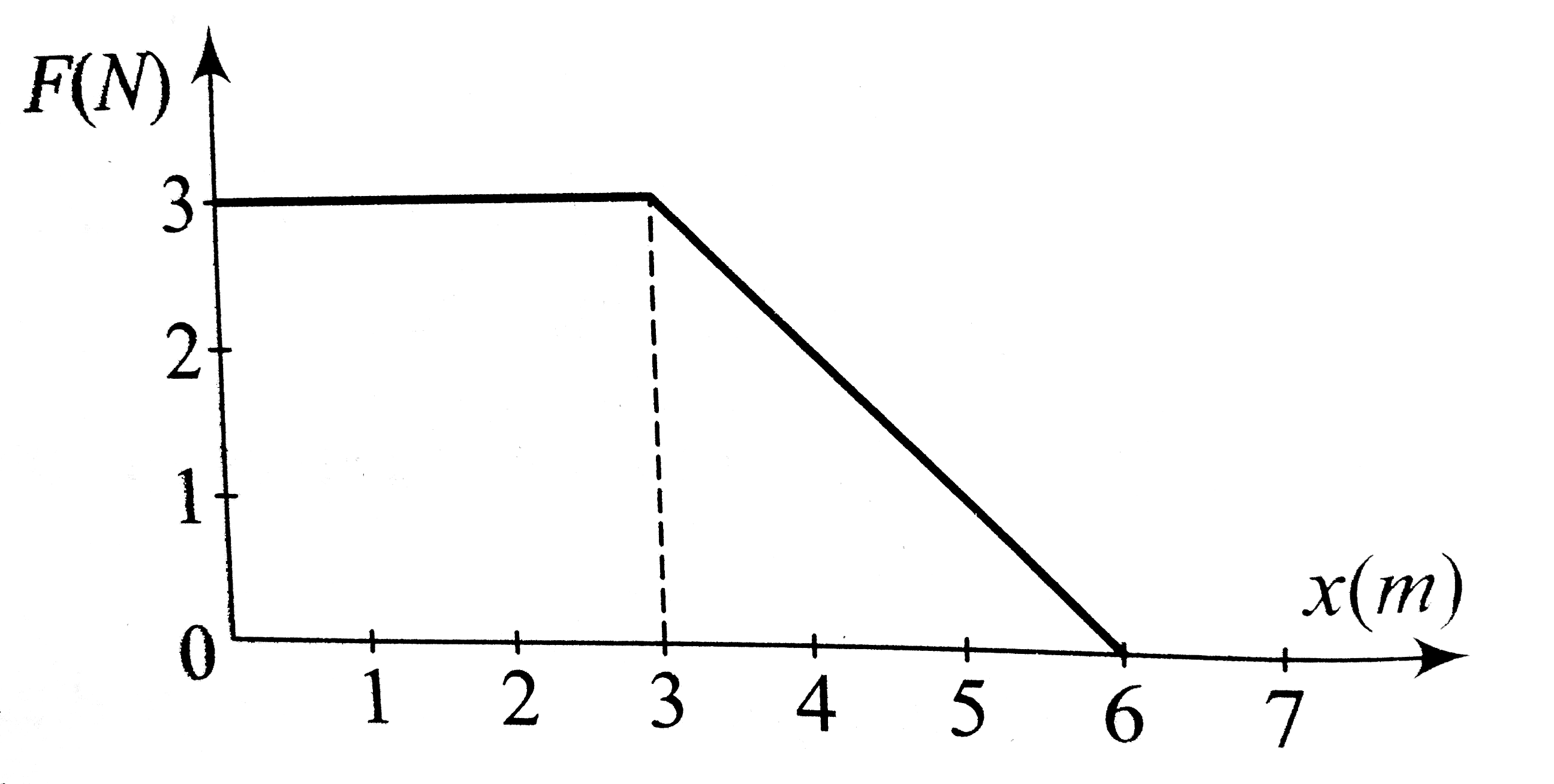
View SolutionA Force `F` acting on an object varies with distance `x` as shown in the here . The force is in newton and `x` in metre. The work done by the force in moving the object from `x = 0` to `x = 6m` is
View SolutionA bomb of mass `30 kg` at rest explodes into two pieces of mass `18 kg` and `12 kg`. The velocity of mass `18 kg` is `6 m//s`. The kinetic energy of the other mass is
View SolutionA particle of mass m1 is moving with a velocity `v_(1)` and another particle of mass `m_(2)` is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are `E_1` and `E_2` respectively. If `m_(1) gt m_(2)` then
View SolutionA ball of mass `2 kg` and another of mass `4 kg` are dropped together from a `60` feet tall building . After a fall of `30` feet each towards earth , their respective kinetic energies will be the ratio of
View SolutionA stone tied to a string of length `L` is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at lowest position and has a speed `u` . Find the magnitude of the change in its velocity as it reaches a position, where the string is horizontal.
View SolutionA stationary partical explodes into two partical of a masses `m_(1) and m_(2)` which move in opposite direction with velocities `v_(1) and v_(2)`. The ratio of their kinetic energies `E_(1)//E_(2)` is
View SolutionIf kinetic energy of a body is increased by 300%, then percentage change in momentum will be
View SolutionA stone is thrown at an angle of `45^(@)` to the horizontal with kinetic energy `K`. The kinetic energy at the highest point is
View SolutionA child is swinging a swing. Minimum and maximum heights fo swing from the earth's surface are 0.75 m and 2 m respectively. The maximum velocity of this swing is
View SolutionTwo bodies with kinetic energies in the ratio 4:1 are moving with equal linear momentum. The ratio of their masses is
View SolutionTwo equal masses `m_1` and `m_2` moving along the same straight line with velocites `+3 m//s` and `- 5 m//s` respectively collide elastically. Their velocities after the collision will be respectively.
View SolutionA foce acts on a 30.g particle in such a way that the position of the particle as a function of time is given by
`x=3t-4t^(2)+t^(3)`, where x is in metre and t in second. The work done during the first 4s is
View SolutionA metal ball of mass 2 kg moving with a velocity of `36km//h` has a head on collision with a stationery ball of mass 3 kg. If after the collision, the two balls move together, the loss in kinetic energy dur to collision is
View SolutionA body of mass m moving with velocity `3km//h` collides with a body of mass 2m at rest. Now, the coalesced mass starts to move with a velocity
View SolutionIf the momentum of a body is increased by 50%, then the percentage increase in its kinetic energy is
View SolutionThe `KE` acquired by a mass m in travelling a certain distance s, starting from rest, under the action of a constant force is directly proportional to :
View SolutionTwo masses 1g and 9g are moving with equal kinetic energies. The ratio of the magnitudes of their respective linear momenta is
View SolutionA force `vecF=(7-2x+3x^(2))` N is applied on a 2 kg mass which displaces it from x = 0 to x = 5 m. Work done in joule is -
View SolutionTwo identical balls `A and B` having velocity of `0.5 m//s and -0.3 m//s` respectively collide elastically in one dimension. The velocities of `B and A` after the collision respectively will be
View SolutionThe power of a motor pump is 2kW. How much water per minute the pump can raise to a heiht of 10 m ? (Given `g = 10 m//s^2)`
View SolutionA bullet of mass 10g leaves a rifle at an intial velocity of 1000m/s and strikes the earth at the same level with a velocity of 500m/s. The work done in joule to overcome the resistance of air will be
View SolutionThe coefficient of restitution e for a perfectly elastic collision is
View Solution
objective questions and complete solutions for chapter WORK, ENERGY AND POWER of NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE) of Class 12