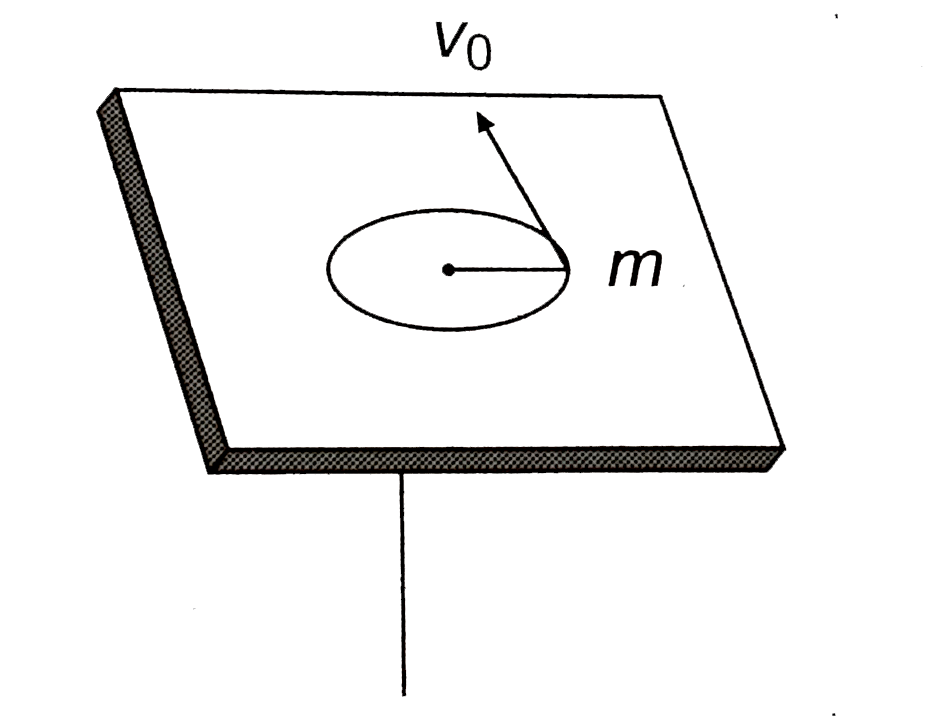
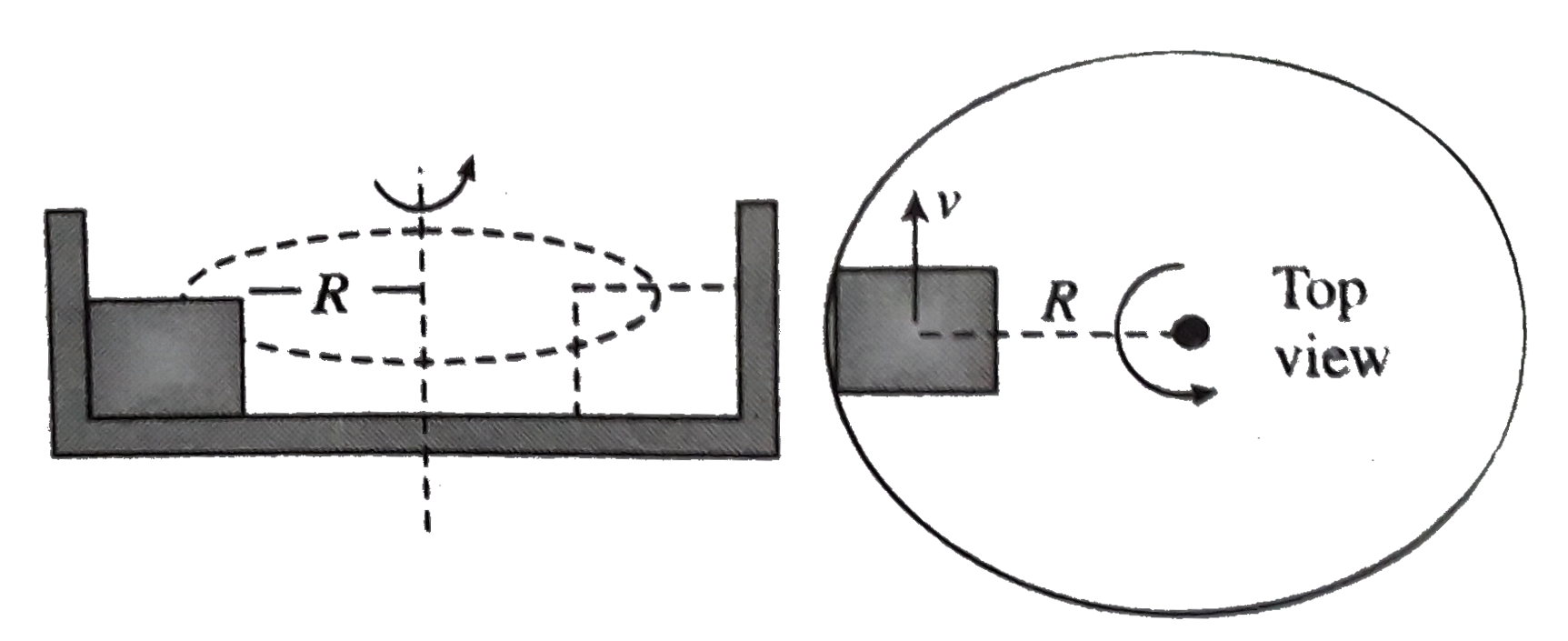
A mass m moves in a circles on a smooth horizontal plane with velocity v0 at a radius R0. The mass is atteched to string which passes through a smooth hole in the plane as shown.
The tension in string is increased gradually and finally m moves in a cricle of radius R02. the final value of the kinetic energy is
mv20
14mv20
2mv20
12mv20
The correct Answer is:c
(c )Conserving angular momemtum
Li=Lf
⇒mv0R0=mv'(R02)
⇒v =2v0
So,final kinetic energy of the particle is
Kf=12mv'2=12m(2v0)2
412mv'2=2mv20
Topper's Solved these Questions
Similar Questions
A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0, The mass is attached to a string which passes through a smooth hole in the plane as shown.
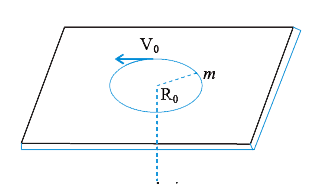
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is :
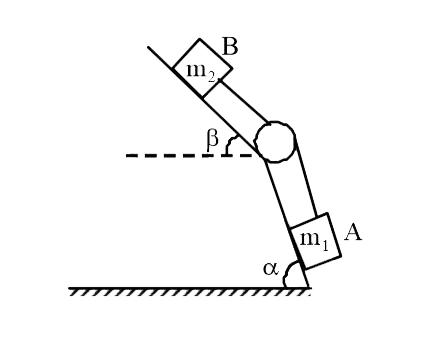
View SolutionTwo blocks A and B of masses m1 and m, are connected by an inextensible string rest on two smooth planes inclined at angle α and β as shown. The tension in string is -
View Solution
Knowledge Check
A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
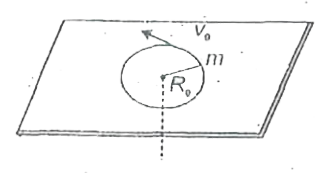
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy isA12mv20Bmv20C14mv20D2mv20A small mass attached to a string rotates on a frictionless table top as shown in Fig. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
 Aremain constantBincrease by a factor of 2Cincrease by a factor of 4Ddecrease by a foctor of 2
Aremain constantBincrease by a factor of 2Cincrease by a factor of 4Ddecrease by a foctor of 2A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A1/2Mv2B3/2Mv2CMv2D1/2MR2ω2
Figure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA small block of mass m on a horizontal smooth table is attached to a light string passing through a hole as shown in the figure. Initially, the block moves in a circle of radius r with speed v and the string is held by a person. The person pulls the strin slowly to decrease the radius of circle to r/2. (a) Find the tension in the string when the block moves in a circle of radius r/2. (b) Calculate the change in the kinetic energy of the block.

View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
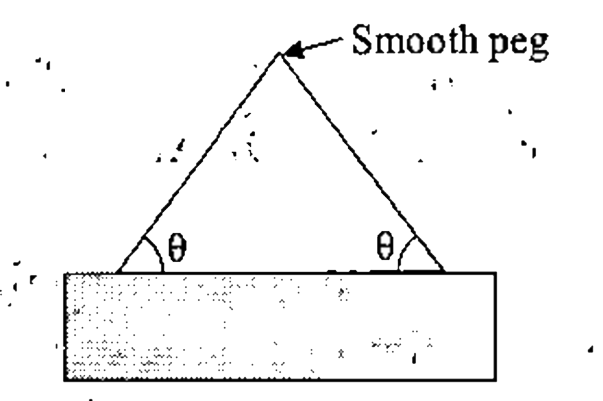
View SolutionA block of mass m is supported by a string passing through a smooth peg as shown in the figure-2.130. Variation of tension in the string T as a function of θ best represented by (here the total length of the string is varied).
View SolutionA point mass m is moved in vertical circle of radius r with help of string. Velocity of mass is 7gr√ at lowest point. Tension in string at lowest point is
View Solution
