Complete Solutions to Exercises of chapter FUNDAMENTAL OF CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FUNDAMENTAL OF CURRENT ELECTRICITY |
| NN GHOSH | Exercises |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
A wire carries a constant current of 10A. How many coulombs and how many charge carriers pass a cross-rection of the wire in 20 seconds? (charge of electron = `1.6 xx 10^(-19)`C
View SolutionTwo batteries of emf `epsilon_(1)` and `epsilon_(2)` produce a current of 1.5 A when they are in opposition and 2.5A when they are in series. Find the ratio of the two emf's.
View SolutionIn a battery of 10 cell supposed to be in series some are wrongly connected. The cells are sealed in a box. When a similar cell is connected in opposition to the battery, the current produced by the combination through an external resistor of `14.5Omega` is 0.075 A. How many cells are wrongly connected? What is the emf of the battery and what is its internal resistance if emf of each cell is 1.5V and internal resistance `0.5Omega`?
View SolutionHow you would arrange 24 cells, each of emf 1.5V and internal resistance `0.5Omega`, to deliver maximum current to a resistor of `4Omega`? What is the maximum current?
View SolutionA letter `A` is constructed as a uniform wire of resistance 1 ohm/cm. The sides of the letter are 20 cm long and the cross piece in the middle is 10 cm long while the vertex angle is `60^(@)` the resistance of the letter between the two ends of the legs is
View SolutionCalculate the the resistivity of the material of a wire whose resistance is `5Omega`, length 1m and radius 0.6mm.
View SolutionThe resistance of 100m of copper wire of diameter `0.056 xx 10^(-2)` m is 6.62`Omega`. Calculate (i) resistivity, (ii) Electrical conductivity of copper.
View SolutionCalcualte the resistance of a steel wire of length 10m and diameter 0.6mm at `0^(@)C` and `100^(@)C`. (Electrical resistivity of steel `0^(@)C` is `15 xx 10^(-8)Omega`m and mean temperature coefficient of resistance of steel is `50 xx 10i^(-4)K^(-1)`
View SolutionThree wires whose lengths are in the ratio `3:8:18` and radii in the ratio `1:2:3` are connected in parallel. Find the ratio of the currents through them.
View SolutionA moving coil galvanometer of resistance `50Omega` is connected in series with a fixed resistance `50Omega` and the combination to a cell of steady emf and negligible internal resistance. What is the shunt required to halve the current through the galvanometer?
View SolutionA resistance box, a battery and a galvanometer of resistance `G` ohm are connected in series. the galvanometer is shunted by resistance of `S` ohm, find the change in resistance in the resistance box be required to maintain the current from the battery unchanged.
View SolutionA shunt is to be applied to a galvanometer of `99Omega` so that only 10% of the total current passes through it. Find the shunt required. What additional shunt will be required to send `1%` of the total current through the galvanometer?
View SolutionTwo identical cells of emf 1.5V and internal resistance `1Omega` are joined in series and the combination is connected in parallel with a third cell of the same emf and internal resistance. Calculalte the terminal voltage of the cells.
View SolutionA battery of emf 6V internal resistance 5`Omega` is joined in parallel with another cell of emf of 10V and internal resistance `1Omega` and the combination is used to send current through a resistor of `12Omega`. Calculate the current through each battery.
View SolutionA battery of emf 6 volts and internal resistance `1Omega` is connected in parallel to another battery of emf 8V and internal resistance `2Omega`. The combination is then used to send current through an external resistance of `10Omega`. Find the current through the external resistance.
View SolutionTwo batteries of emfs 24V and 6V and internal resistance `2Omega` and `1Omega` respectively are joined in parallel, negative to negarive by a resistor of `2Omega` and positive to positive by another resistor of `4Omega.` Calculate the terminal voltages of the two batteries.
View SolutionThe sides of a square ABCD are formed of wires, each of resistance r and B is joined to D by a wire of resistance 2r. Find the equivalent resistance of the skelton
(i) between B and D, (ii) between A and C and (iii) between A and B.
View SolutionIn a wheatstone bridge, the resistance of the arms of the bridge are AB = `2Omega`, BC = `4Omega` ,AD = `1Omega` and DC = `3Omega`. The terminals of negligible resistance to A and C. If a galvanometer of resistance `100Omega` is connected between B and D, find the current in the galvanometer.
View SolutionABCD is a square of side a meters and is mae up of wires of resistance `xOmega//m`. Similar wires are connected across the diagonals AC and BD. Show that the effective resistance of the frame-work between the corners A and C is `(2-2sqrt(2)` ax `Omega`.
View SolutionA battery of 2V and internal resistance `2Omega` is used in wheatstone bridge. Find the current through the galvanometer in the unbalanced position of the bridge when `P=1Omega`, `Q=2Omega`,`R=2Omega`,`S=3Omega` and `G=4Omega`.
View SolutionWhen one mole of zinc combines with sulphuric acid 445 kJ of heat is liberated and when a mole of copper is liberated from blue vitriol 235 kj of heat is absorbed. Avogadro number = `6.023 xx 10^(23)`, electronic charge = `1.6 xx 10^(-19)` C and zinc or copper is divalent. Use these data to find the emf of a Daniell cell.
[Hint: Energy liberated in the form of heat is converted into elecrical energy in a Daniel cell]`
View SolutionTwo resistors with temperature coefficients of resistance `alpha_1` and `alpha_2` have resistances `R_(01)` and `R_(02) ` at `0^@C`. Find the temperature coefficient of the compound resistor consisting of the two resistors connected.
a.. In series and
b. in paralllel
View SolutionShow that if E is the electric intensity inside a conductor of electrical conductivity `sigma`, Ohm's law may be coveniently put in the form, `vec(J) = sigmavec(E )` where J = current density in the conductor.
View SolutionShow that drift velocity of electrons in a conductor is given by u = `J/(ne)` where J is the current density, n is the number of mobile electrons per unit volume and e is the charge carried by each electron. Calculate the same in a copper wire of radius of 0.6mm when a current of 1A flows through it assuming that one mobile electron is available from one atom of copper. Atomic weight of copper = 63.55, density of copper = 8930 kgm^(-3)`, Avogadro number = `6.01 xx 10^(26)`Kg `mol^(-1)` and e = `1.6 xx 10^(-19)`C
View SolutionA spherical silver electrode of radius 8cm is concentric with a spherical metal shell of radius 10cm. The inter space contains an insulating material of resistivity `10^(6)Omega`m. Compute the resistance of the insulator.
[Hint: Resistance of a shell of radius z = `rho(dz)/(4piz^(2)`. Integrate from z = 8 to z=100
View SolutionTwo batteries of emf 12V and 6V and internal resistance `2Omega` and `1Omega` are connected in parallel and the combination is connected to a resisor of `2Omega` through a key. Find the potential difference between the positive and negative terminals of the batteries (a) When key is open, b) when key is closed. Find the emf and internal resistance of a single cell which would be equivalent to the combination.
View SolutionFind the potential difference the points a and b of the circuit(figure). If a and b are joined by a wire what is the current through the 12-V cell?
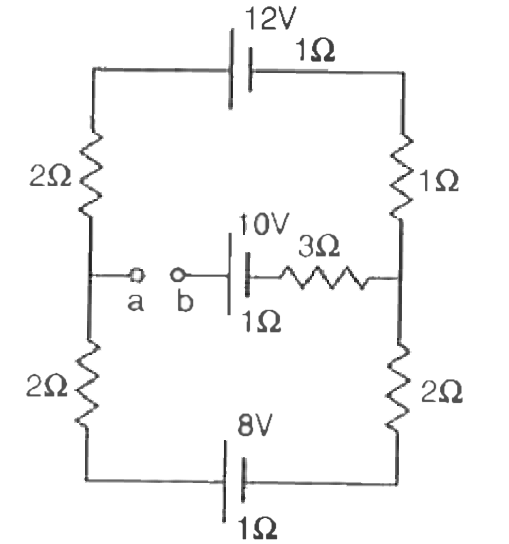
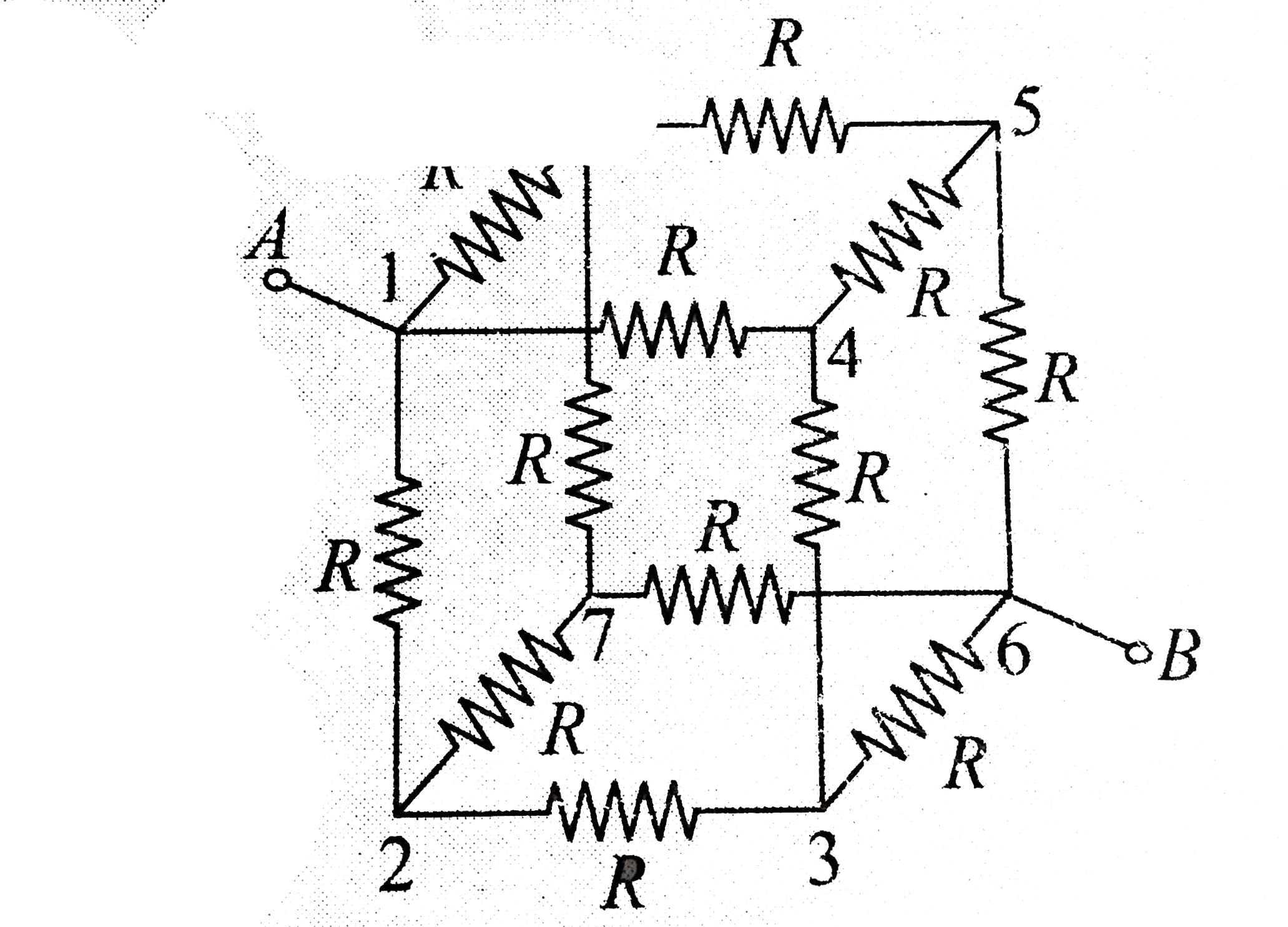
View SolutionTwelve identical resistor are arranged on all edges of a cube. Then find the equivalent resistance between the corners 1 and 6 as shown in fig 5.126(use nodal method) .
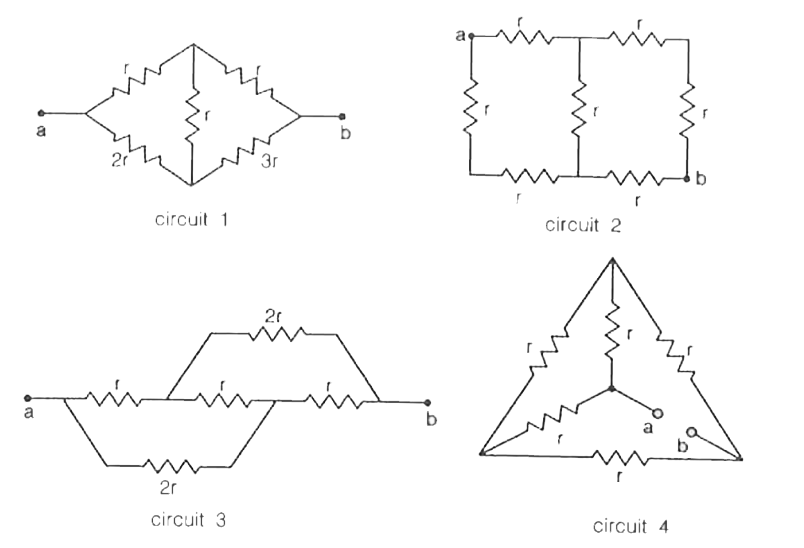
View SolutionFind the equivalent resistance between the terminal points a and b of the circuits 1, 2,3 and 4.
View SolutionA newtwork of conductors is in the form of a triangle ABC in which AB = `1Omega`, BC=`2Omega` and CA = `3Omega` and the angular points A, B and C are joined to any point O inside the triangle by resistance `1Omega`, `2Omega` and `3Omega`, respectively. Find the equivalent resistance between A and B.
[Hing: Assume current at the entrance and exit points].
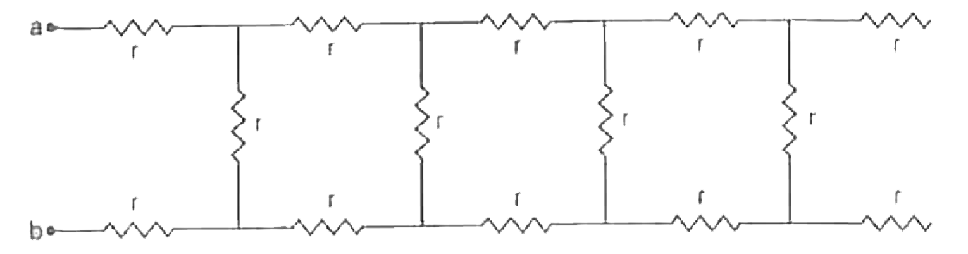
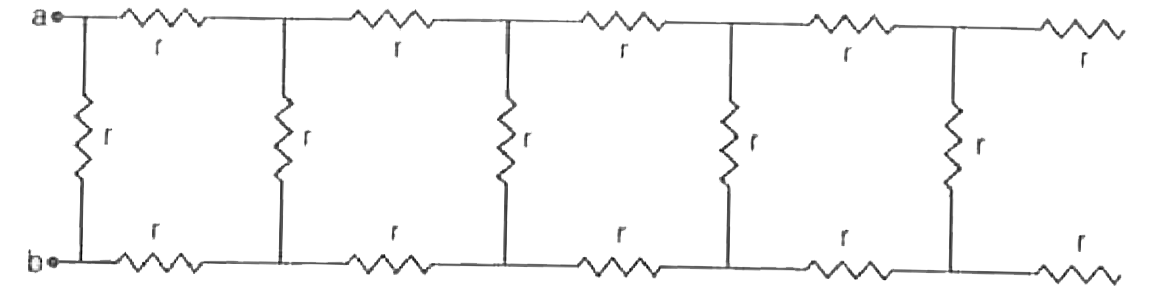
View SolutionFind the resistance of the infinite series of the circuit in figure between the points a and b.
[Hint: From an infinite series if we separate out the first unit, the remaining circuit will still be an infinite series and hence will have the same equivalent resistance]
View SolutionCalculate the equivalent resistance of the circuit shown in figure between the points a and b.
View SolutionA current of 8A is to be sent through a resistor of `5Omega` Calcualte the least number of cells required for the purpose when each cell has emf 2V and internal resistance `0.5Omega`.
View SolutionN cells, each of emf `epsilon` and internal resistance r, are arranged in a ring in series. Two points including n cells on one side and N-n cells on the other side are connected to a resistor R. Calcualte the current through R (figure)

View SolutionCalcualte the equivalent resistance between the terminals of the cell (figure) The resistance of each equivalent is `1Omega` and the intersecting diameters have resistance `2Omega` each.
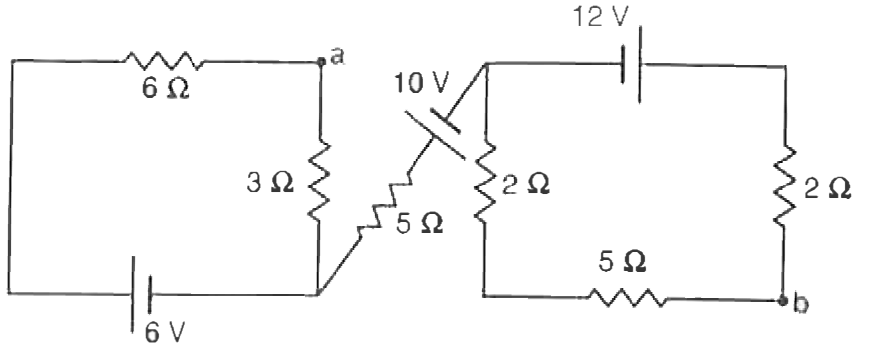
View SolutionFind the potential difference between the point a,b of the given circuit figure. [Hint: `V_(ab)= sumir-sumepsilon`]
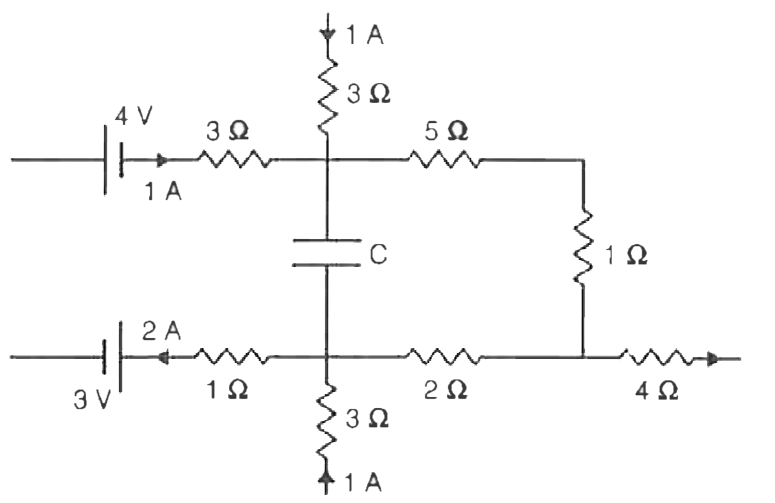
View SolutionA part of a circuit in the steady state with the currents flowing in the branches and the values of resistance are shown in figure. Calculate the energy stored in the capacitor `C=4muF`.
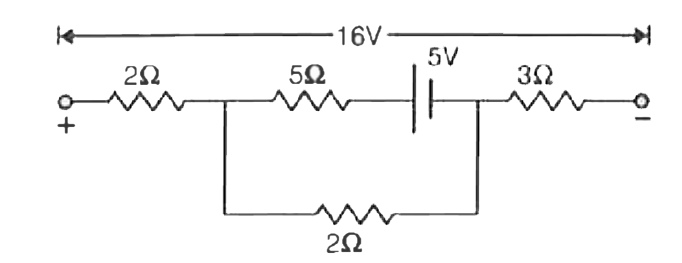
View SolutionCalculate the current through the 5-V cell of the figure.
View SolutionIn the circuit in figure there are n repetitions of the same loop. What resistance should be connected across the end points so that the equivalent resistance between a and b may be independent of n? What is this equal to?
View SolutionThere is an infinite wire grid with square cells (Fig). The resistance of each wire between neighbouring joint connections is equal to `R_(0)` . Find the resistance `R` of the whole grid between points `A` and `B`.
Instruction. Make use of principles of symmetry and superposition.

View SolutionTwo metals balls of the same radius a are placed in a homogenous poorly conducting media with resistivity `rho`. Find the resistance if they are separated by a large distance.
[Hint: Use `j=sigmaE` to evaluate total current through mid-plane and then use V=IR]
View SolutionShow that if one collision takes place in every `tau` seconds then the resistivity is given by `rho=(m)/(ne^(2)rho`, where all the terms have their usual meaning.
View SolutionA straight copper-wire of length `100m` and cross-sectional area `1.0mm^(2)` carries a current `4.5A`. Assuming that one free electron corresponds to each copper atom, find
(a) The time it takes an electron to displace from one end of the wire to the other.
(b) The sum of electrostatic forces acting on all free electrons in the given wire. Given resistivity of copper is `1.72xx10^(-8)Omega-m` and density of copper is `8.96g//cm^(3)`.
View SolutionA constant voltage is applied to n groups of resistors in siries where each group has m identical resistros in parallel. One resistor burns out in one group. Find the percentage increase of current in each resistor of the faulty group, and the percentage decrease of current in each resistor of the second group.
View SolutionIf `alpha_(1)` is the temperature coefficient of resistance at `t_(1)^(@)C` find `alpha_(2)` at `t_(2)^(@)C`
[hint: `alpha`=1/R(dR)/dt)` and `R=R_(0)(1+at+btp^(2))]`
View Solution
Exercises questions and complete solutions for chapter FUNDAMENTAL OF CURRENT ELECTRICITY of NN GHOSH PHYSICS (HINGLISH) of Class 12