Complete Solutions to एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.4)) of chapter सम्बन्ध एवं फलन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | सम्बन्ध एवं फलन |
| MADHUR GUPTA | एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.4)) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
निर्धारित कीजिए कि क्या निम्नलिखित प्रकार से परिभाषित प्रत्येक संक्रिया `**` से एक द्विआधारी संक्रिया प्राप्त होती है या नहीं । उस दशा में जब `**` एक द्विआधारी संक्रिया नहीं है, औचित्य भी बतलाइए ।
(i) `Z^(+)` में, `a**b=a-b` द्वारा परिभाषित संक्रिया `**`
(ii) `Z^(+)` में, `a**b=ab`द्वारा परिभाषित संक्रिया `**`
(iii)R में, संक्रिया `**,a**b=ab^(2)`द्वारा परिभाषित
(iv) `Z^(+)` में संक्रिया `**,a**b=|a-b|`द्वारा परिभाषित
(v) `Z^(+)` में, , संक्रिया `**,a**b=a`द्वारा परिभाषित
View Solutionनिम्नलिखित परिभाषित प्रत्येक द्विआधारी संक्रिया `**` के लिए निर्धारित कीजिए कि क्या `**` द्विआधारी क्रमविनिमेय है तथा क्या `**` साहचर्य है ।
(i) Z में, `a**b=a-b` द्वारा परिभाषित
(ii) Q में,`a**b=ab+1` द्वारा परिभषित
(iii) Q में, `a**b=(ab)/(2)` द्वारा परिभाषित
(iv) `Z^(+)`में, `a**b=2^(ab)`द्वारा परिभाषित
(v) `Z^(+)` में , `a**b=a^(b)`द्वारा परिभाषित
(vi) `R-{-1}` में , `a**b=(a)/(b+1)`द्वारा परिभाषित
View Solutionसमुच्चय {1,2,3,4,5} में `a^^b=` निम्नतम `{a,b}` द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए । संक्रिया `^^` के लिए संक्रिया सारणी लिखिए ।
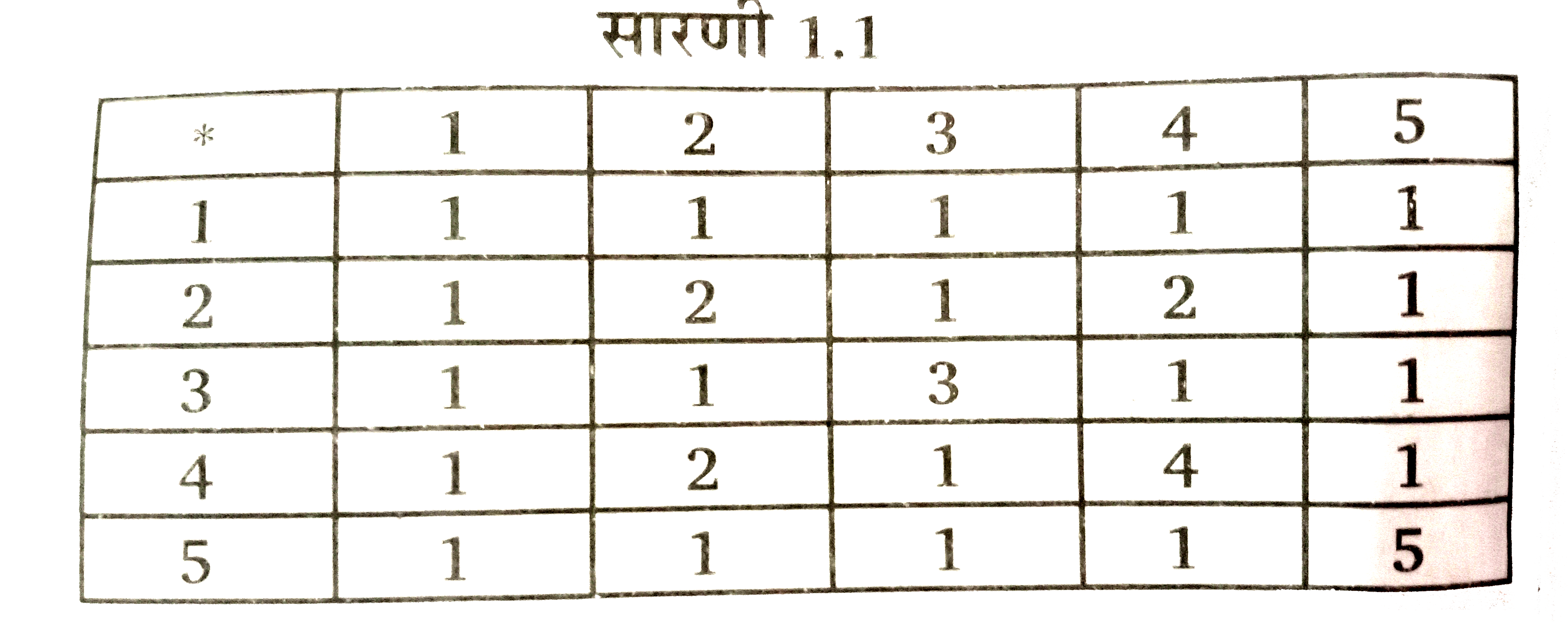
View Solutionसमुच्चय `{1,2,3,4,5}` में , निम्नलिखित संक्रिया सारणी (सारणी 1.1) द्वारा परिभाषित द्विआधारी संक्रिया `**` पर विचार कीजिए तथा
(i) `(2**3)**4` तथा `2**(3**4)` का परिकलन कीजिए ।
(ii) क्या `**` क्रमविनिमेय है ?
(iii) `(2**3)**(4**5)`का परिकलन कीजिए ।
( संकेत : निम्न सारणी का प्रयोग कीजिए ।)
सारणी 1.1
View Solutionमान लीजिए कि समुच्चय {1,2,3,4,5} में एक द्विआधारी संक्रिया `**',a**'b=a` तथा b का HCF द्वारा परिभाषित है । क्या संक्रिया `**'` उर्पयुक्त प्रश्न 4 में परिभाषित संक्रिया `**` के समान है ? अपने उत्तर का औचित्य भी बतलाइए ।
View Solutionमान लीजिए कि N में एक द्विआधारी संक्रिया `**, a**b = a ` तथा b का LCM द्वारा परिभाषित है । निम्नलिखित ज्ञात कीजिए :
(i) `5**7, 20**16`
(ii) क्या संक्रिया `**` क्रमविनिमेय है?
(iii) क्या `**` साहचर्य है ?
(iv) N में `**` का तत्समक अवयव ज्ञात कीजिए।
(v) N के कौन से अवयव `**` संक्रिया के लिए व्युत्क्रमणीय हैं ?
View Solutionक्या समुच्चय `{1,2,3,4,5}` में `a**b=a` तथा b का LCM द्वारा परिभाषित `**`एक द्विआधारी संक्रिया है ? अपने उत्तर का औचित्य भी बतलाइए ।
View Solutionमान लीजिए कि N में `a**b=a` तथा b का H.C.F. द्वारा परिभाषित एक द्विआधारी संक्रिया है । क्या `**`क्रमविनिमेय है ? क्या `**` साहचर्य है ? क्या N में इस द्विआधारी संक्रिया के तत्समक का अस्तित्व है ?
View Solutionमान लीजिए कि परिमेय संख्याओं के समुच्चय Q में निम्नलिखित प्रकार से परिभाषित `**` एक द्विआधारी संक्रिया है :
(i) `a**b=a-b " " (ii) a**b=a^(2)+b^(2)`
(iii) `a**b=a+ab " " (iv) a**b=(a-b)^(2)`
(v) `a**b=(a^(b))/(4) " " (vi) a**b=ab^(2)`
ज्ञात कीजिए कि इनमें से कौन-सी संक्रियाएँ क्रमविनिमेय हैं और कौन - सी साहचर्य हैं ?
View Solutionप्रश्न 9 में दी गई संक्रियाओं में किसी का तत्समक है , वह बतलाइए ।
View Solutionमान लीजिए कि `A=NxxN` है तथा A में `(a,b)**(c,d)=(a+c,+b+d)`द्वारा परिभाषित एक द्विआधारी क्रिया है । सिद्ध कीजिए कि `**` क्रमविनिमेय तथा साहचर्य है । A में `**`का तत्समक अवयव, यदि कोई है, तो ज्ञात कीजिए ।
View Solutionबतलाइए कि क्या निम्नलिखित कथन सत्य हैं या असत्य हैं ? औचित्य भी बतलाइए ।
(i) समुच्चय N में किसी भी स्वेच्छ द्विआधारी संक्रिया `**` के लिए `a**a=a,AA a in N`
(ii) यदि N में `**` एक क्रमविनिमेय द्विआधारी संक्रिया है, तो `a**(b**c)=(c**b)**a`
View Solution`a**b=a^(3)+b^(3)` प्रकार से परिभाषित N में के द्विआधारी संक्रिया `**` पर विचार कीजिए । अब निम्नलिखित में से सही उत्तर का चयन कीजिए :
(a) `**` साहचर्य तथा क्रमविनिमेय दोनों है
(b) `**`क्रमविनिमेय है किन्तु साहचर्य नहीं है
(c) `**` साहचर्य है किन्तु क्रमविनिमेय नहीं है
(d) `**`न तो क्रमविनिमेय है और न साहचर्य है
View Solution
एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.4)) questions and complete solutions for chapter सम्बन्ध एवं फलन of NAGEEN MATHS (HINDI) of Class 12
All Exercises from MADHUR GUPTA Class 12 MATHS सम्बन्ध एवं फलन
- एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.1))
- एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.2))
- एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.3))
- एन० सी० आर० टी० प्रश्न (प्रश्नावली (1.4))
- प्रश्नावली (1A)
- प्रश्नावली (1B)
- प्रश्नावली (1C)
- प्रश्नावली (1D) (बहुविकल्पीय प्रश्न )
- प्रश्नावली (1E) (विविध प्रतियोगी परीक्षाओं हेतु प्रश्न )
- विविध प्रश्नावली
- साधित उदाहरण