Complete Solutions to MATHEMATICS of chapter NTA JEE MOCK TEST 61 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | NTA JEE MOCK TEST 61 |
| NTA MOCK TEST | MATHEMATICS |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
The coefficients of `x^(13)` in the expansion of
` (1 - x)^(5) (1 + x + x^(2) + x^(3) )^(4)` , is
View SolutionA bag contains 30 tokens numbered serially from 0 to 29. The number of ways of choosing 3 tokens from the bag, such that the sum on them is 30, is
View SolutionNumber of roots of the equation `2sqrt(2x+1)=2x-1` is 0 (b) 1 (c) 2 (d) 3
View SolutionLet the `n^(th)` term of a series be given by `t_n = (n^2 -n-2)/(n^2+3n),n leq 3`. Then product `t_3 t_4 .....t_50` is equal to
View SolutionThe value of `lim_(nrarroo)(1^(2)-2^(2)+3^(2)-4^(2)+5^(2)….+(2n+1)^(2))/(n^(2))` is equal to
View SolutionTwo ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is `10(sqrt3+1)` meters and their angle of elevations of the top of the lighthouse are `60^(@) and 45^(@)`, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
View SolutionIf `[sin^(-1)x]^(2)-2[sin^(-1)x]+1le0` (where, [.] represents the greatest integral part of x), then
View SolutionLet `f:R rarr R` be a function defined as `f(x)=(x^(2)-6)/(x^(2)+2)`, then f is
View SolutionIf the variate of a distribution takes the values `1^(2), 2^(2), 3^(2),….n^(2)` with frequencies `n, n-1, n-2,….3,2,1` respectively, then the mean value of the distribution is
View SolutionThe point of intersection of tangents drawn to the hyperbola `(x^2)/(a^2)-(y^2)/(b^2)=1` at the points where it is intersected by the line `l x+m y+n=0` , is `((-a^2l)/n ,(b^2m)/n)` (b) `((-a^2l)/m ,(b^2n)/m)` `((a^2l)/m ,(-b^2n)/m)` (d) `((a^2l)/m ,(b^2n)/m)`
View SolutionThe value of the integral `int_(0)^(pi)(e^(|cosx|)sinx)/(1+e^(cotx))dx` is equal to
View SolutionThe curve `y=f(x)` in the first quadrant is such that the y - intercept of the tangent drawn at any point P is equal to twice the ordinate of P If `y=f(x)` passes through `Q(2, 3)`, then the equation of the curve is
View SolutionThe value of the integral `I=int(2x^(9)+x^(10))/((x^(2)+x^(3))^(3))dx` is equal to (where, C is the constant of integration)
View SolutionIf A, B and C are square matrices of same order and I is an identity matrix of the same order, such that `C^(2)=CB+AC and AB=I`, then `(C-A)^(-1)` is equal to
View SolutionThe system of equations `alpha(x-1)+y+z=-1, x+alpha(y-1)+z=-1 and x+y+alpha(z-1)=-1` has no solution, if `alpha` is equal to
View SolutionIf vectors `4vecp+vecq, 2 vecp-3vecq and 5vecp-3vecq, 5vecp+3vecq` are a pair of mutually perpendicular vectors and if the angle between `vecp and vecq` is `theta`, then the value of `sin^(2)theta` is equal to
View SolutionThe equation of the plane through the points (2,-1,0), (3,-4,5) parallel to a line with direction cosines proportional to 2,3,4 is 9x-2y-3z=k, where k is
View SolutionThe line `2x+3y=12` meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
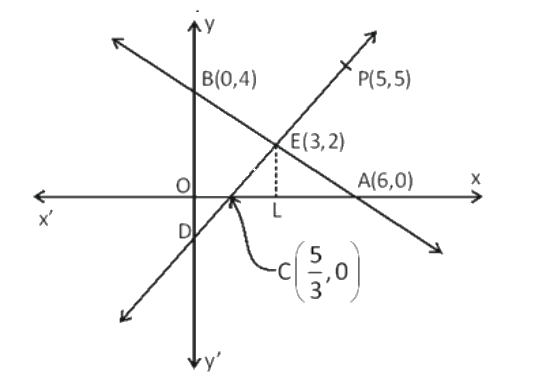
View SolutionThe extremities of a diagonal of a rectangle which are parallel to the diagonal are
View SolutionThe ordinates of points P and Q on the parabola `y^2=12x` are in the ration 1:2 . Find the locus of the point of intersection of the normals to the parabola at P and Q.
View SolutionThe area (in sq. untis) bounded by `[x+y]=2` with the co - ordinate axes is equal to (where `[.]` denotes the greatest integer function)
View SolutionOut of 1000 boys in a school, 300 played cricket, 380 played hockey and 420 played basketball. Of the total, 120 played both basketball and hockey,100 played cricket and basketball, 70 played cricket and hockey and 56 played all the three games. If the probability of the number of boys who did not play any game is k, then 200k is equal to
View SolutionIf `4cos36^(@)+cot(7(1^(@))/(2))=sqrt(n_(1))+sqrt(n_(2))+sqrt(n_(3))+sqrt(n_(4))+sqrt(n_(5))+sqrt(n_(6))`, then the value of `((Sigma_(i=1)^(6)n_(i)^(2))/(10))` is equal to
View SolutionThe number of solution of `x^(3)+4x-1=0` in the interval `x in(-2,1)` is
View SolutionFor the complex number Z, the sum of all the solutions of `Z^(2)+|Z|=(barZ)^(2)` is equal to
View Solution
MATHEMATICS questions and complete solutions for chapter NTA JEE MOCK TEST 61 of NTA MOCK TESTS of Class 12