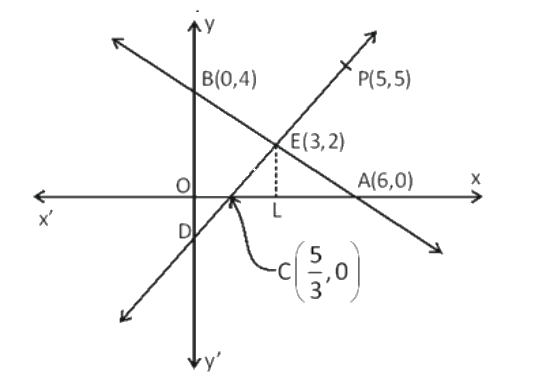
The line 2x+3y=12 meets the coordinates axes at A and B respectively.

The plane $2 x + 3 y + 4 z = 12$ meets the coordinate axes in A,B and C. The centroid of $△ A B C$ is
A(2,3,4)
B(6,4,3)
C $(2, \frac{4}{3}, 1)$
Dnone of these
Straight line $2 x + 3 y + 10 = 0$ inersects coordinate axes respectively are the points
A $(- 5, 0) (0, - \frac{10}{3})$
B $(\frac{10}{3}, 0) (0, 5)$
C $(- 5, 0), (0, \frac{10}{3})$
D $(\frac{- 10}{3}, 0), (0, \frac{- 5}{3})$
A line $L_{1} = \frac{x}{10} + \frac{y}{8} = 1$ intersects the coordinate axes at points A and B. Another line $L_{2}$ perpendicular to $L_{1}$ intersects the coordinate axes at C and D. The locus of circumcentre of $Δ A B D$ is
A $5 x - 4 y = 9$
B $5 x - 4 y = 18$
C $4 x - 5 y = 9$
D $4 x - 5 y = 18$

The line $2 x + 3 y = 12$ meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to