Complete Solutions to MATHEMATICS of chapter NTA TPC JEE MAIN TEST 67 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | NTA TPC JEE MAIN TEST 67 |
| NTA MOCK TESTS | MATHEMATICS |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
If for the complex number `z_1 and z_2, abs(z_1+z_2)=abs(z_1-z_2)` is equal to
View SolutionIf `Delta_1 = abs({:(1,1,1),(a,b,c),(a^2,b^2,c^2):}),Delta_2= abs({:(1,a,bc),(1,b,ca),(1,c,ab):})" then"`
View SolutionThe number of ways in which a mixed doubles game can be arranged from amongst n couples such that no husband and wife play in the same game is
(Note : Mixed doubles is a match in which a man and a woman play as partners against another man and woman.)View SolutionIf `S_n=1/(1.3.4)+1/(2.4.5)+…` then `+1/(n(n+2)(n+3))`
`limS_n` is equal to `n to oo`View SolutionIf the chords of the hyperbola `x^(2) – y^(2) = 16` touches the parabola `y^(2) = 16x`, then the locus of the middle points of these chords is a curve
View SolutionLet A (-2, 2) and B (2,-2) be two points. P is a variable point such that area of `Delta PAB` is 8 then locus of P is
View SolutionThe distance of point of intersection of lines `(x-4)/1=(y+3)/(-4)=(z+1)/7 and (x-1)/2=(y+1)/(-3)=(z+10)/8` from (1, -4,7), is
View SolutionGiven `abs(veca)-abs(vecb)=1 and abs(veca+vecb)=sqrt3, "if" vec c` be a vector such that `vecc-veca-2vecb=3(veca xx vecb),`, then `vecc.vecb` is equal to
View Solutionlet
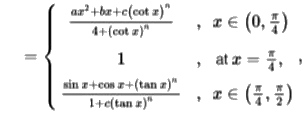 where a, b, c are real constants and `f(x)=lim_(n to oo)g(x).` If
where a, b, c are real constants and `f(x)=lim_(n to oo)g(x).` If
`lim_(x to pi/4)` f(x) exists, then c may be `x to pi/4` equal toView SolutionIf `f(x)` be differentiable function and curve `y=f(x)` passes through (1, 1) and satisfies the relation `2f(x+y)+f(x-y)+3y^2` then `=3f(x)+2xy`, `lim_(x to 1)(f(x)-1)/(x-1)` is equal to
View SolutionIf `2ysinx(dy)/(dx)=sin2x-y^2 cosx and at x=pi/2,y=1`, then
View SolutionIf `int((x^2-x+1)/(x^2+1)).e^(cot^(-1)x)dx=A(x).e^(cot^-1x)+C,` where C is constant of integration, then A(x) is equal to
View SolutionThe value of x in (0, `pi/2`) satisfying equation `(sqrt5-1)/(sinx)+sqrt(10+2sqrt5)/cos x`=8` is
View SolutionRectangle ABCD has area 200 sq. unit. An ellipse with area `200 pi`. unit passes through A and C has focii at B and D. Then perimeter of the rectangle ABCD is
View SolutionNumber of solutions of the equations `y=1/3[sinx+[sin x + [sin x]]] and [y+[y]]=2 cos x`, where [.] denotes the greatest integer function is:
View SolutionIf `sin^(-1)(2a)/(1+a^2)+sin^-1""(2b)/(1+b^2)` then x is `=2 ta^-1 x,`
equal toView SolutionIf the line `2x+y+k=0` is a mormal to the parabola `y^2+8x=0`, then the value of k is
View SolutionThe coefficient of variation of 10 observations, if the sum of squares of deviations taken from their mean 50 is 250, is
View SolutionThe logical proposition `(~(~p vv q) vv (p ^^ r)) ^^ (~q ^^ r)` is equicalent to
View SolutionThe area enclosed by `y=g(x)," "x=-3," "x=5` and x-axis where g(x) is the inverse of `f(x)=x^3+3x+1` is
View SolutionThe expansion of `(1+x+x^2)^n` is `a_0+a_1x+a_(2)x^(2)+ … +a_(2n)x^(2n)`. Find the value of `(a_0+a_1+a_3+a_4+….)/(a_2+a_5+a_8 +….)=`
View SolutionIf `{:[((-1+isqrt3)/(2i),(-1,isqrt3)/(2i)),((i+isqrt3)/(2i),(1 - isqrt3)/(2i))]:}, i = sqrt(-1) and f(x) =x ^2 + 2` Then `abs(f(A)/((2 + isqrt3)))` is equal to
View SolutionFor the quadratic equation `6x^2+11x+3=0`, if `alpha and beta` are the roots, then the value of `(6alpha+11)^2+(6beta+11)^2` is
View Solutionif `5f(x)+3f(1/x)=x+2` and `y=x f(x)`, then `((dy)/(dx))_(x=1)` is equal
View SolutionFind the length of PQ such that the tangent at the point P on the circle `x^2+y^2+6x+6y=2` meets the straight line `5x-2y+6=0` at a point Q on the y-axis.
View SolutionA `2 xx 2` matrix is fromed with entries from the set `{0, 1}`, The probability that it is singular is
View SolutionLet f be a function defined on R such that
`f^'(x)=2018(x-2017)(x-2018)^2`
`(x-2020)^4.(x-2019)^3` for all `x in R`. If g is a function defined an R, with values in `(0, oo)` such that `g(x)=e^(f(x))` for all `x in R,` then the numder of points of reletive aptima will be:View SolutionIf `2x=y^(1/3)+y^(-1/3),(x^2-1)y^('')+xy^'`
`=ky`
k is equal to.View SolutionThe velue of `overset(pi/2)underset(0)int (1+cos3x)/(2 cos x-1)dx` is:
View SolutionThe lines `x+y=0, x-4y=0 and 2x-y=0` are the altitudes of a triangle. If one of the altitudes of a triangle. If one of the vertices has the coordinates (`-lambda, lambda`) and the locus of the centroid of this triangle is `ax+by=0` (where a and b are positive intergers and coprime to each other), then the value of (a+2b) is
View Solution
MATHEMATICS questions and complete solutions for chapter NTA TPC JEE MAIN TEST 67 of NTA MOCK TESTS of Class 12
