Complete Solutions to Illustrative Example of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| PHYSICS GALAXY | Illustrative Example |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
If the average life time of an excited state of hydrogen is of the order of `10^(-8) s`, estimate how many whits an alectron makes when it is in the state `n = 2` and before it suffers a transition to state` n = 1 (Bohrredius a_(0) = 5.3 xx 10^(-11)m)`?
View SolutionWhat is the angular momentum of an electron in Bohr's hydrogen atom whose energy is `-3.4e V`?
View SolutionThe electron in a hydrogen atom makes a transition `n_(1) rarr n_(2)`, where `n_(1)` and `n_(2)` are the principle quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. the possible values of `n_(1)` and `n_(2)` are
View SolutionHow many time does the electron go round the first bohr orbit of hydrogen atoms in `1 s`?
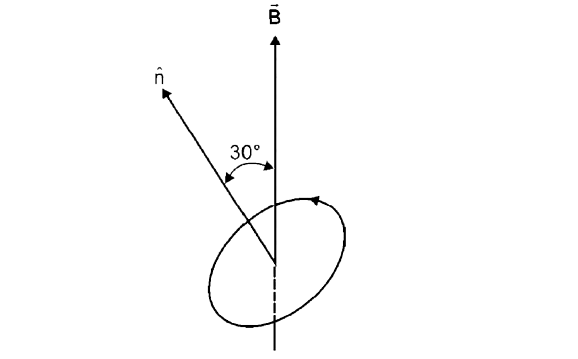
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius `R`.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction `vec(B)` such that the plane - normal of the electron - orbit makes an angle of ` 30^(@)` with the magnetic induction . Find the torque experienced by the orbiting electron.
View SolutionDetermine the minimum wavelength that hydrogen in its ground state can obsorb. What would be the next smaller wavelength that would work?
View SolutionIf the wavelength of the first member of Balmer series in hydrogen spectrum is 6563 Å, calculate the wavelength of the first member of Lymen series in the same spectrum.
View SolutionThe ratio of ionization energy of Bohr's hydrogen atom and Bohr's hydrogen-like lithium atom is
View SolutionElectron of energies 10.20 eV and 12.09 eV` can cause radiation to be emitted from hydrogen atoms . Calculate in each case, the principal quantum number of the orbit to which electron in the hydrogen atom is raised and the wavelength of the radiation emitted if it drops back to the ground state.
View SolutionDetermine the wavelength of the first Lymanline,the transition from `n=2"to"n=1`.In what region of the electromagnetic spectrum does this line lie ?
View SolutionHydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength `970.6 Å`. How many lines are possible in the resulting emission spectrum ? Calculate the longest wavelength amongst them. You may assume that the ionisation energy for hydrogen atom is 13.6 eV. Given Planck's constant `= 6.6 xx 10^(-34)Js, " " c = 3 xx 10(8) ms^(-1)`
View SolutionA hydrogen atom in a state having a binding energy of 0.85 eV makes transition to a state with excitation energy 10.2 eV. The quantum number n of the upper and the lower energy states are
View SolutionUltraviolet light of wavelength `800 A` and `700 A` when allowed to fall on hydrogen atoms in their ground states is found to liberate electrons with kinetic energies `1.8eV` and `4.0eV`, respectively. Find the value of Planck's constant.
View SolutionThe ionization energy of a hydrogen like bohr atom is `4` Rydbergs (i) What is the wavelength of the radiation emitted when the electron jumps from the first excited state to the ground state ?(ii) what is the radius of the orbit for this atom ?
View SolutionEstimate the average kinetic energy of hydrogen atoms (or molecules) at room temperature and use the result to explain why nearly all H atom sare in the ground state at room temperature and hence emit no light.
View SolutionThe emission spectrum of hydrogen atoms has two has two lines of Balmer series with wavelength `4102Å`and `4861Å`. To what series does a spectral line belong if its wave nmnber is equal to the difference of wave number is of above two lines ? What is the wavelength of this line? `[TakeR=1.097xx10^(7)m^(-1)]`
View SolutionTwo hydrogen-like atoms `A` and `B` are of different masses and each atom contains equal numbers of protons and neutrons. The difference in the energies between the first Balmer lines emitted by `A and B` , is `5.667 e V`. When atom atoms `A and B` moving with the same velocity , strike a heavy target , they rebound with the same velocity in the process, atom `B` imparts twice the momentum to the target than that `A` imparts. Identify the atom `A and B`.
View SolutionA hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
View SolutionA single electron orbit around a stationary nucleus of charge `+ Ze` where Z is a constant and e is the magnitude of the electronic charge. It requires`47.2 eV` to excite the electron from the second bohr orbit to the third bohr orbit. Find
(i) The value of Z
(ii) The energy requiredto nucleus the electron from the third to the fourth bohr orbit
(iii) The wavelength of the electronmagnetic radiation required to remove the electron from the first bohr orbit to inlinity
(iv) The energy potential energy potential energy and the angular momentum of the electron in the first bohr orbit
(v) The radius of the first bohr orbit (The ionization energy of hydrogen atom ` = 13.6 eV ` bohr radius `= 5.3 xx 10^(-11) matre` velocity of light `= 3 xx 10^(8) m//sec` planks 's constant ` = 6.6 xx 10^(-34)` jules - sec )
View SolutionA gas of identical hydrogen-like atoms has some atoms in the lowest in lower (ground) energy level `A` and some atoms in a partical upper (excited) energy level `B` and there are no atoms in any other energy level.The atoms of the gas make transition to higher energy level by absorbing monochromatic light of photon energy `2.7 e V`.
Subsequenty , the atom emit radiation of only six different photon energies. Some of the emitted photons have energy `2.7 e V` some have energy more , and some have less than `2.7 e V`.
a Find the principal quantum number of the intially excited level `B`
b Find the ionization energy for the gas atoms.
c Find the maximum and the minimum energies of the emitted photons.
View SolutionCalculate the separation between the particles of a systemin the ground state, the corresponding binding energy and wavelength of first line in Lyman series of such a system is positronium consisting of an electron and positron revolvin ground their common centre.
View SolutionA `mu-meson` ("charge -e , mass `= 207 m`, where m is mass of electron") can be captured by a proton to form a hydrogen - like ''mesic'' atom. Calculate the radius of the first Bohr orbit , the binding energy and the wavelength of the line in the Lyman series for such an atom. The mass of the proton is `1836` times the mass of the electron. The radius of the first Bohr orbit and the binding energy of hydrogen are `0.529 Å` and `13.6 e V` , repectively. Take `R = 1.67 xx 109678 cm^(-1)`
View SolutionA particle of charge equal to that of an electron - e, and mass 208 times the mass of electron (called a mu meson) moves in a circular orbit around a nucleus of charge` + 3e` (Take the mass of the nucleus to be infinite) Assuming that the bohr model of the atom is applicable to this system
(i) Derive an expression for the radius of the bohr orbit
(ii) find the value for which the radius is approximately the same as that of the bohr orbit fo the hydrogen atom
(iii) find the wavelength of the radiation emitted when the mu- meson jump from the third orbit of the first orbit
View SolutionA `pi-meason` hydrogen atom is a bound state of negative charged pion (denoted by `pi^(bar), m_(pi) = 273 m_(e))` and a proton. Estimate the number of revolutions a `pi-meason` makes (averagely ) in the ground state on the atom before , it decays (mean life of a `pi-meason ~= 10^(-8) s`, mass of proton `= 1.67 xx 10^(-27) kg)`.
View SolutionTaking into account the motion of the nucleus of a hydrogen atom , find the expressions for the electron's binding energy in the ground state and for the Rydberg constant. How much (in percent) do the binding energy and the Rydberg constant , obtained without taking into account corresponding values of these of these quantities?
View SolutionCalculate difference in binding energy of atomic hydrogen and atomic deuterium.
View SolutionA muan is an unstable elementary partical whose mass `(mu^(-))` can be captured by a hydrogen nucleus (or proton) to from a muonic atom.
a Find the redius of the first Bohr orbit of this atom.
b Find the ionization energy of the atom.
View SolutionSuppose the potential energy between an electron and aproton at a distance `r` is given by `-Ke^(2)// 3 r^(3)`. Use Bohr's theory to obtain energy level of such a hypothetical atom.
View SolutionAssume a hypothetical hydrogen atom in which the potential energy between electron and proton at separation r is given by `U = [k ln r - (k/2)],` where k is a constant. For such a hypothetical hydrogen atom, calculate the radius of nth Bohr orbit and energy levels.
View SolutionSuppose a moving hydrogen atom makes a head on inelastic collision with a stationary hydrogen atom. Before collision, both atoms are ground state and after collision, they move together. What is the minimum velocity of the moving hydrogen atom if one of the atoms is to be given the minimum excitation energy after the collisions? Take `m_H=1.0078 am u. 1 am u =1.66xx10^(-27)kg.`
View SolutionA neutron of kinetic `6.5 eV` collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle `90^(@)` with respect to its original direction.
Find the maximum allowed value of energy of the He atom?
View SolutionAn electron having energy `20 e V` collides with a hydrogen atom in the ground state. As a result of the colllision , the atom is excite to a higher energy state and the electron is scattered with reduced velocity. The atom subsequentily returns to its ground state with emission of rediation of wavelength `1.216 xx 10^(-7) m`. Find the velocity of the scattered electron.
View SolutionAccording to classical physics, an electron in periodic motion with emit electromagnetic radiation with the same frequency as that of its revolution. Compute this value for hydrogen atom in nth quantum theory permit emission of such photons due to transition between adjoining orbits ? Discuss the result obtained.
View SolutionA `100 eV` electron collides with a stationary helium ion `(He^(+))` in its ground state and excites to a higher level. After the collision , `He^(+)` ion emits two photons in succession with wavelength `1085 Å and 304 Å`. Find the principal quantum number of the excite in its ground state and. Also calculate energy of the electron after the collision. Given `h = 6.63 xx 10^(-34) J s`.
View Solution
Illustrative Example questions and complete solutions for chapter ATOMIC PHYSICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12