Complete Solutions to NumericalMCQsSingle OptiorisCorrect of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| PHYSICS GALAXY | NumericalMCQsSingle OptiorisCorrect |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
The energy required to excite a hydrogen atom from `n= 1` to `n = 2` energy state 10.2 eV. What is the wavelength of the radiation emitted by the atom when it goes back to Its ground state ?
View SolutionConsider Bohr's theory for hydrogen atom.The magnitude of angular momentum, orbit radius and frequency of the electron in `n^(th)` energy statein a hydrogen atom are L,r & f espectively. Find out the value of 'x', if the product f r L is directly proportional to `n^(th)`:
View SolutionFor the first member of Balmer series of hydrogen spectrum, the wavelength is `lamda`. What is the wavelength of the second member?
View SolutionIn a new system of units the fundamental quantities are planks constant (h), speed of light `("c")` and time (7). Then the dimensions of Rydberg's constant will be :
View SolutionIn a hypothetical atom, if transition from `n=4` to `n=3` produces visible light then the possible transition to obtain infrared radiation is:
View SolutionIf first excitation potential of a hydrogen like-atom is V electron volt, then the ionization energy of this atom will be:
View Solutionlonisatiori energy for hydrogen atom in the ground state is E.What is the ionisation energy of `Li^(++)` atom in the `2^(nd)` excited state?
View SolutionThe different lines in the Lyman series have their wavelengths laying between:
View SolutionThe orbital electron of the hydrogen atom jumps from the ground state to a higher energy state and its orbital velocity is reduced to one third of its initial value. If the radius of the orbit in the ground state is r, then what is the radius of the new orbit ?
View SolutionIf we assume that penetrating power of any radiation/particle is inversely proportional to its de-Broglie wavelength of the particle then :
View SolutionAccording to Bohr's theory the ratio of time taken by electron to complete one revolution in first excited and second excited states of hydrogen will be:
View SolutionThe area of the electron orbit for the ground state of hydrogen atom is A.What will be the area of the electron orbit corresponding to the first excited state ?
View SolutionIf the wave-number of a spectral line of Brackett series of hydrogen is `(9)/(400)` times the Rydberg constant.What is the state from which the transition has taken place ?
View SolutionThe ionization potential of H-atom is 13.6 V. The H-atoms in ground state are excited by mono chromatic radiations of photon energy 12.09 ev. Then the number of spectral lines emitted by the excited atoms, will be
View SolutionAn electron jumps from the first excited state to the ground stage of hydrogen atom..What will be the percentage change in the speed of electron ?
View SolutionAn energy of `24.6 eV` is required to remove one of that electrons from a neutal helium atom. The enegy (in `eV`)required to remove both the electrons from a netural helium atom is
View SolutionA neutron beam, in which each neutron has same kinetic energy, is passed through a sample of hydrogen like gas (but not hydrogen) in ground state and at rest. Due to collision of neutrons with the ions of the gas, ions are excited and then they emit photons. Six spectral lines are obtained in which one of the lines is of wavelength (6200/51) nm.Which gas is this?
View SolutionIn previous questiom what is the minimum possible value of kinetic energy of the neutrons for this to be possible. The mass of neutron and proton can be assumed to be nearly same. Use `hc=12400 eVÅ`
View SolutionIn Millikan's oil drop experiment, a charged oil drop of mass `3.2xx10^(-14)kg` is held stationary between two parallel plates 6mm apart by applying a potential difference of `1200 V` between them. How many excess electrons does the oil drop carry? Take `g =10ms^(-2)`
View SolutionIn a hydrogen like atom the energy required to excite the electron from `2^(nd)` to `3^(rd)` orbit is `47.2 eV` What is atomic number of the atom?
View SolutionTwo hydrogen atoms are in excited state with electrons in`n=2` state.First one is moving to wards left and emits a photon.' of energy `E_(1)` towards right. Second one is moving towards right with same speed and emits a photon of energy `E_(2)` towards right. Taking recoil of nucleus.into account during_emission process :
View SolutionIn a hydrogen atom following the Bohr's postulates the product of linear momentum and angular momentum is proportional to `n^(x)` where 'n' is the orbit number. Then 'x' is:
View SolutionThe velocityof an electron in second orbit of tenly ionized sodium atom (atomic number Z= 11) is v. The velocity of an electron in its fifth orbit will be:
View SolutionA positronium consists of an electron and a positron revolving about their common centre of mass. Calculate the separation between the electron and positron in their first excited state:
View SolutionA positronium atom consist of an electron and a positron revolving about their common centre of mass . Calculate
Kinetic energy of the electron in ground state
View SolutionA hydrogen atom ia in excited state of principal quantum number `n` . It emits a photon of wavelength `lambda` when it returnesto the ground state. The value of `n` is
View SolutionThe ratio of the binding energies of the hydrogen atom in the first and the second excited states is
View SolutionMonochromatic radiation of wavelength `lambda` is incident on a hydrogen sample in ground state. hydrogen atoms absorb a fraction of light and subsequently and radiation of six different wavelength .Find the value of `lambda`
View SolutionOut of the following transitions, the frequency of emitted photon will be maximurn for.:
View SolutionImagine a neutral particle of same mass m as electron revolving around a proton of mass `M_(p)` only under newton's gravitational force. Assuming Bohr's quantum condition, the radius of electron orbit is given by:
View SolutionDetermine the ratio of perimeters in `2^(nd)` and `3^(rd)` Bohr orbit in`He^(+)` atom:
View Solutionthe photon radiated from hydrogen corresponding to the second line of Lyman series is absorbed by a hydrogen like atom X in the second excited state. Then, the hydrogen-like atom X makes a transition of nth orbit.
View SolutionAn `alpha`-particle with a kinetic energy of `2.1eV` makes a head on collision with a hydrogen atom moving towards it with a kinetic energy of `8.4 eV`. The collision
View SolutionA hydrogen atom is initially atrest and free to moveis in the second excited state.It comes to ground state by emitting a photon, then the momentum of hydrogen atom will be approximately: (in `kg-m//s`)
View SolutionAn gas of H-atom in excited state `n_(2)` absorbs a photon of some energy and jump in hiegher energy state `n_(1)`. Then it returns to ground state afer emitted six different wavelengths in emission spectrum. The energy of emitted photon is equal, less or greater than the energy of absorbed photon then `n_(1)` and `n_(2)` will be
View SolutionImagine an atom made of a proton and a hypothetical particle of double the mass of the electron but having the same change as the electron. Apply the Bohr atom model and consider all possible transitions of this hypothetical particle of the first excited level. the longest wavelength photon that will be emitted has wavelength [given in terms of the Rydberg constant `R` for the hydrogen atom] equal to
View SolutionOne of the lines in the emission spectrum of `Li^(2+)` has the same wavelength as that of the `2nd` line of Balmer series in hydrogen spectrum. The electronic transition corresponding to this line is:
View SolutionIn Bohr's theory the potential energy of an electron at a position is `(Kr^(2))/(2)` (where Also is a positive constant), then the quantized energy of the electron in nth orbit is:
View SolutionIf first and second frequencies in transition to orbital are related by the relation `v_(1)=kv_(2)` then the first frequency in the transition to second orbital will notbe equal to :
View SolutionThe ratio of de-Broglie wave length of a photon and an electron of mass 'm' having the same kinetic energy E is: (Speed of light=c)
View SolutionA monochromatic radiation of wavelength `lambda` is incident on a sample containig `He+`. As a result the Helium sample stars radiating. A part of this radiation is allowed to pass through a sample of atomic hydrogen gas in ground state. It is noticed that the hydrogen sample has stared emitting electrons whose maximum kinetic energy is `37.4 eV`.
`(hc = 12400 eV Å)`. Then `lambda` is
View SolutionOf the following transitions in a hydrogen atom, the one which gives an absorption line of highest frequency is
View SolutionAn electron of the kinetic energy `10 eV` collides with a hydrogen atom in `1st` excited state. Assuming loss of kinetic energy in the collision be to quantized which of the following statements is correct?
View SolutionIf the first orbit of a hydrogen atom the total energy of the electron is `-21.76 xx 10^(-19)J`, then its electric potential energy will be:
View SolutionIn the figure six lines of emission spectrum are shown. Which of them will be absent in the absorption spectrum.
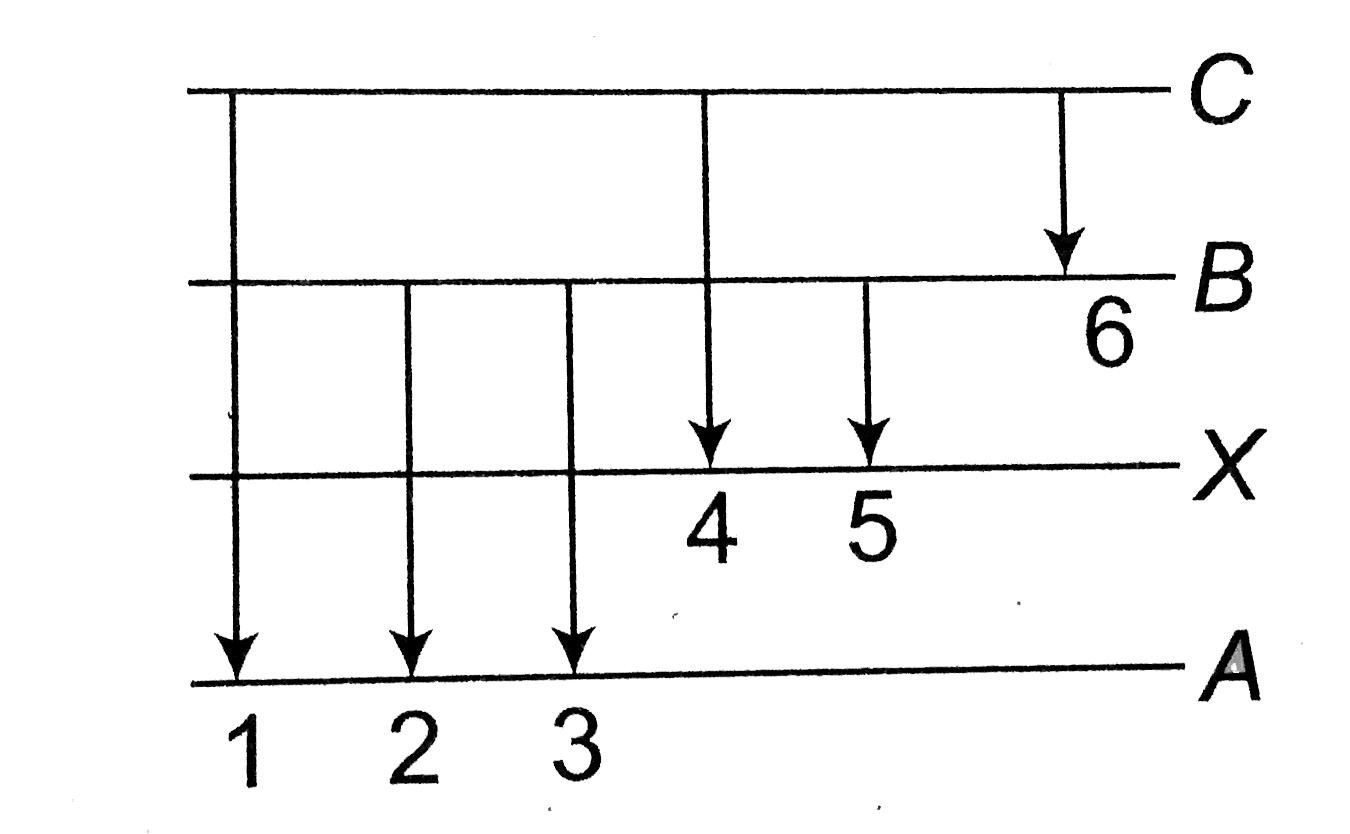
View SolutionAn orbit electron in the ground state of hydrogen has an angular momentum `L_(1)`, and an orbital electron in the first orbit in the ground state of lithium (dounle ionised positively) has an angular momentum `L_(2)`. Then :
View SolutionThe ratio of the maximum wavlength of the Lyman series in hydrogen specturm to the maximum wavelength in the Panchen series is
View SolutionConsider atoms `H, He^(+), Li^(++)` in their ground states. Suppose `E_(1), E_(2)` and `E_(3)` are minimum energies required so that the atoms `H He^(+), Li^(++)` can achieve their first excited states respectively, then
View SolutionThe radius of first Bohr orbit of hydrogen atom is `0.53Å`. Then the radius of first Bohr-orbit of mesnoic atom (negative meson has mass 207 times that of electron but same charge) is:
View Solution
NumericalMCQsSingle OptiorisCorrect questions and complete solutions for chapter ATOMIC PHYSICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12