Complete Solutions to Exercise of chapter ATOMS AND NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMS AND NUCLEI |
| PRADEEP | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Planck's constant has the dimension (unit) of
View SolutionWhat is the ground state energy of electron in case of `Li^(2+)` ?
View SolutionWhat is the order of velocity of electron in a hydrogen atom in ground state?
View SolutionThe ratio of radii of orbits correponding to first and second excited states of hydrogen atom is
View SolutionWhat is the ionisation potential of hydrogen atom?
View SolutionWhich one of the series of hydrogen spectrum is in the visible region ?
View SolutionThe correct relation for impact parameter, where symbols have their usual meaning is
View SolutionThe diameter of first orbit of hydrogen atom is of the order of
View SolutionTotal energy of electron in nth stationary orbit of hydrogen atom is
View SolutionWhat is the value of Rydberg constant?
View SolutionA coording to Thomson model, the entire mass and positive charge of an atom are distributed.............in a..............of radius.......... .
View SolutionThe size of atomic nucleus is of the order of............ m and size of the atom is of the order of........... .
View SolutionTotal energy of electron in orbit of an atom is............. .This indicates that electron............ .
View SolutionLyman series lies in............region and Balmer series lies in.......... region of hydrogen spectrum.
View SolutionAccording to Bohr, angular momentum...............in hydrogen atom is........... .
View SolutionThe radii of stationary orbits are in the ratio............ .
View SolutionOrbital velocity of electron is outer orbits is............as compared to its value in............. .
View SolutionIn the first stationary orbit of hydrogen atom, the frequency of revolution of electron is of the order of.............. , and energy of electron is of order............ .
View SolutionTotal energy of electron in outer orbits is........that in............. .
View SolutionAn `alpha` particle of `K.E. 10^(-12)J` exibits back scattering form a gold nucleus Z=79. What can be the maximum possible radius of the gold nucleus?
View SolutionA beam of `alpha`-particle of velocity `2.1xx10^(7)m//s` is scattered by a gold ofil (Z=79). Find the distance of closest approach of `alpha`- particle to the gold nucleus. for `alpha`-particle, `2e//m=4.8xx10^(7)kg^(-1)`.
View SolutionIn a head on collision between an alpha particle and gold nucleus, the minimum distance of approach is `4xx10^(-14)m`. Calculate the energy of of `alpha`-particle. Take Z=79 for gold.
View SolutionCalculate the impact parameter of a 5MeV alpha particle scattered by `10^@` when it approaches a gold nucleus. Take Z=79 for gold.
View SolutionAn alpha particle of energy 4MeV is scattered through an angle of `180^(@)` by a gold foil (Z=79). Calculate the maximum volume in which positive charge of the atom is likely to be concetrated?
View SolutionThe number of alpha particles scattered at `60^(@)` is 100 per minute in an alpha particle scattering experiment. Calculate the number of alpha particles scattered per minute at `90^(@)`.
View SolutionCalculate the impact parameter of a 5 MeV particle scattered by `90^(@)`, when it approach a gold nucleus (Z=79).
View Solutionfor scattering by an inverse square law field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle `theta` is given by
`b=(Ze^2 cot theta//2)/(4pi in_0(1/2mv^2))`
(a) What is the scattering angle for b=0?
(b) for given impact parameter, b, does the angle of deflection increase or decrease with increase in energy?
(c) What is the impact parameter at which the scattering angle is `90^@` for Z=79 and initial energy=10MeV?
(d) Why is it that the mass of the nucleus does not enter the formula above, but its charge does?
(e) for a given energy of the projectile, does the scattering angle increase or decrease with decrease in impact parameter?
View SolutionAn alpha particle having KE equal to `8.7MeV` is projected towards the nucleus of copper with Z=29. Calculate its distance of closest approach.
View SolutionThe ground state energy of hydrogen atom is `-13.6eV`. If an electron makes a transition form an energy level `-0.85 eV` to `-3.4 eV`, calculate the wavelength of spectral line emitted. To which series of hydrogen spectrum does this wavelength belongs?
View SolutionThe ground state energy of hydrogen atom is -13.6eV. If an electron makes a transition form an energy level -0.85 eV to -1.51 eV, calculate the wavelength of spectral line emitted. To which series of hydrogen spectrum does this wavelength belongs?
View SolutionThe ground state energy of hydrogen atom is -13.6 eV (i) What are the potential energy and K.E. of electron is 3rd excited state?
(ii) If the electron jumped to the ground state form the third excited state, calculate the frequency of photon emitted.
View SolutionAt what speed must an electron revolve around the nucleus of hydrogen atom so that it may not be pulled into the nucleus by electrostatic attraction? Given, mass of electron `=9.1xx10^(-31) kg`, radius of orbit `=0.5xx10^(-10)m and e=1.6xx10^(-19)C.`
View SolutionCalculate the frequency of revolution of electron in the second Bohr's orbit of radius 2.12Å. Given, `h=6.6xx10^(-34)Js, m=9xx10^(-31)kg`.
View SolutionDetermine the radius of the first orbit of hydrogen atom. What would be the velocity and frequency of electron in this orbit? Given `h=6.6xx10^(-34)Js, m=9xx10^(-31)kg , e=1.6xx10^(-19)C, K=9xx10^(9)Nm^(2)C^(-2)`.
View SolutionThe wavelength of first members of Lyman series is `1216A^(@)`. Calculate the wavelength of 3rd member of Paschen series.
View SolutionThe wavelength of `K_(alpha)` line for copper is `1.36^(@)`. Calculate the ionisation potential of a K shell electron in copper.
View SolutionCalculate the longest and shortest wavelength in the Balmer series of hydrogen atom. Given Rydberg constant =`1.0987xx10^7m^-1`.
View SolutionCalculate longest wavelength of Paschen series. Given `R=1.097xx10^(7)m^(-1)`.
View SolutionThe seond line of Balmer series has wavelength `4861 Å` The wavelength o fthe first line Balmer series is
View SolutionThe Rydberg constant for hydrogen is `1.097xx10^(7)m^(-1)`. Calculate the short and long wavelength limits of Lyman series.
View SolutionCalculate the wavelength of photon emitted when an electron jumps form 3rd orbit to 2nd orbit. Take `R=1.097xx10^(7)m^(-1)`. Is the photon visible ?
View SolutionThe ionisation energy of hydrogen atom is 13.6 eV. Calculate Rydberg's constant for hydrogen.
View SolutionEnergy of an electron in an excited hydrogen atom is `-3.4eV`. Its angualr momentum will be: `h = 6.626 xx 10^(-34) J-s`.
View SolutionA hydrogen atom initially in the ground level absorbs a photon, Which excites it to n=4 level. Determine the wavelength and frequency of photon.
View SolutionA `12.9 eV` beam of electrons is used to bombard gaseous hydrogen atom at room temperature. Up to which energy level the hydrogen atoms would be excited?
Calculate the wavelength of the first member of Paschen series and first member of Balmer series.
View SolutionFig. shows energy level diagram of hydrogen atom. Find out the transition which results in the emission of a photon of wavelength 496 nm. Which transition corresponds to emission of radiation of maximum wavelength? Justify your answer.
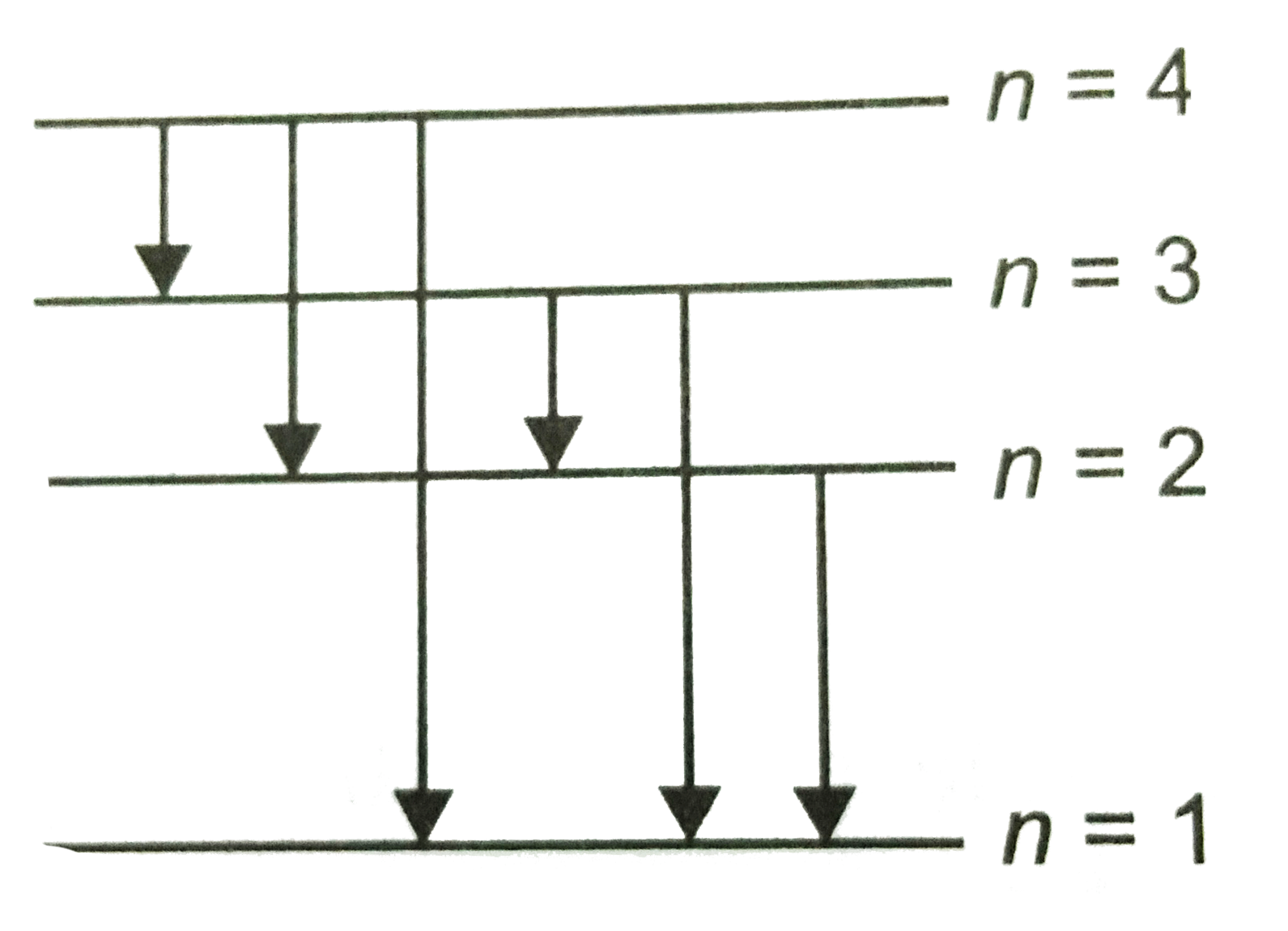
View SolutionA hydrogen atom rises form its n=1 state to the n=4 state by absorbing energy. If the potential energy of the atom in the n=1 state be -13.6 eV, then calculate
(a) potential energy in the n=4 state,
(b) energy obserbed by the atom in transition,
(c) Wavelength of the emitted radiation if the atom returns to its original state.
View SolutionIf in nature they may not be an element for which the principle quantum number `n gt 4`, then the total possible number of elements will be
View SolutionWhich state of the triply ionized `Be^(+++)` has the same orbital radius as that of the ground state of hydrogen? Compare the energies of two states.
View SolutionWhat is the relation between decay constant and half life of a radio active element?
View Solution1curei=k disintegrations/sec, where k is
View SolutionWhich of the following is in the increasing order for penetrating power ?
View SolutionTwo nuclei have mass number in the ratio 1:8. What is the ratio of their nuclear radii?
View SolutionA nucleus `._nX^M` emits one `alpha` particle and one `beta`-particle. What are the mass number and atomic number of the product nucleus?
View SolutionSelect the pairs of isobars and isotones form the following nuclei `._6C^(14),._7N^(13),._7N^(14),._8O^(16)`:
View SolutionCalculate the energy equivalent of 1 a.m.u. in `MeV`
View SolutionOne electron volt is the...........when accelerated through a............. .
View SolutionIsotopes of an element are the atoms ........... which have............. but........... .
View SolutionIsobars are atoms of..........Which have same............... But different .............. .
View SolutionIsotones are the nuclides which contain............ .
View SolutionNuclear forces are the ...............which hold together..............in the tiny ............. .
View SolutionFind the effective mass of a photon if the wavelength of radiation is `6xx10^(14)Hz`.
View SolutionNatural Chlorine is found to be a mixutre of two isotopes of masses 34.98 a.m.u and 36.98 a.m.u. respectively. Their relative abundances are 75.4 and 24.6% respectively. Find the composite atomic mass of natural chlorine.
View SolutionHow many electrons protons, and neutrons are there in `12 g` of `._(6) C^2` and in `14g` of `._(6) C^(14)` ?.
View SolutionCalculate the density of hydrogen nucleus in SI units, given `R_(0)=1.2` fermi, mass of a proton=1.007825 a.m.u.
View SolutionCalculate the equivalent energy of electrons and proton at rest. Given that mass of electron `=9.1xx10^(-31)kg` and mass of proton `=1.673xx10^(-27)kg`.
View SolutionAssuming that protons and neutrons have equal masses, calculate how many times nuclear matter is denser than water. Take mass of a nucleon `=1.67xx10^(-27)kg and R_(0)=1.2xx10^(-15)m`.
View SolutionIf radius of the `_(13)^(27) Al` necleus is estimated to be `3.6` fermi then the radius of `_(52)^(125)Te` nucleus be nearly
View SolutionThe nuclear radius of `._(8)O^(16)` is `3 xx10^(-15) m`. If an atomic mass unit is `1.67 xx 10^(-27) kg`, then the nuclear density is approximately.
View SolutionCalculate the radius of oxygen nucleus. Take `R_(0)=1.1xx10^(-15)m and A=16`
View SolutionThe binding energy of `._(10)Ne^(20)` is 160.6 MeV. Find its atomic mass. Take mass of proton =1.007825 u and mass of neutron =1.008665 u.
View SolutionThe binding energies of deutron `(._1H^2)` and `alpha`-particle `(._2He^4)` are 1.25 and 7.2 MeV/nucleon respectively. Which nucleus is more stable? Calculate binding energy per nucleon of `._(26)Fe^(56). M(._(26)Fe^(56))`=55.934939 a.m.u, m(proton)=1.007825 a.m.u., m(neutron) =1.008665 a.m.u.
View SolutionWhat energy is needed to split an alpha particle to piece? Given mass of `alpha` particle is 4.0039a.m.u, mass of proton=1.007825u and mass of neutron =1.008665u use `1a.m.u.=931MeV`
View SolutionThe binding energy per nucleon for `._(6)C^(12) is 7.68 MeV//N` and that for `._(6)C^(13) is 7.47MeV//N`. Calculate the energy required to remove a neutron form `._(6)C^(13)`
View SolutionCalculate the B.E./nucleon of `._17Cl^(35)` nucleus. Given that of proton `=1.007825u`, mass of neutron `=1.008665 u`, mass of `._17Cl^(35)=34.980000u , 1u=931MeV`.
View SolutionAssuming that in a star, three alpha particle join in a single fusion reaction to form `._(6)C^(12)` nucleus. Calculate the energy released in this reaction. Given mass of `._(2)He^(4)` is 4.002604 a.m.u. and that of `._(6)C^(12)` is 12 a.m.u. Take 1a.m.u. =931MeV.
View SolutionThe sun is believed to be getting its energy form the fusion of four protons to form a helium nucleus and a pair of positrons. Calculate the release of energy per fusion in MeV. Mass of proton=1.007825 a.m.u. , mass of positron =0.000549 a.m.u., mass of helium nucleus =4.002603 a.m.u. Take 1a.m.u. =931MeV.
View SolutionCalculate the binding energy per nucleon in the nuclei of `._(15)P^(31)`. Given `m(._(15)P^(31))=30.97376u, m(._(0)n^(1))=1.00865 u, m(._(1)H^(1))=1.00782u`.
View SolutionThe mass of a `a_3^7 Li` nucleus is `0.042 u` less than the sum of the masses of all its nucleons. The binding energy per nucleon of `._3^7 Li` nucleus is nearly.
View SolutionIf mass of proton =1.007825 u, mass of neutron =1.008665 u, and mass of `._(3)Li^(7)` is 7.01599u, and 1a.m.u. =931MeV, what is BE/nucleon of `._(3)Li^(7)`.
View SolutionA heavy nucleus X of mass number `240` and binding energy per nucleon `7.6 MeV` is split into two fragments Y and Z of mass numbers `110` and `130`. The binding energy of nucleons in Y and Z is `8.5MeV` per nucleon. Calculate the energy Q released per fission in MeV.
View SolutionCalculate the half life periode of a radioactive substance if its activity drops to `1/16` th of its initial value of 30 yr.
View SolutionThe half life of a radioactive substance is 20s. Calculate (i) the decay constant, and (ii) time take by the sample to decay by `7//8th` of its inital value
View SolutionA radioactive isotope has a half life of 5 yrs. How long will it take the activity to reduce to `3.125%`?
View SolutionHalf life of a certain radioactive material is 100 days. After how much time the undecayed fraction of material will be 6.25%?
View SolutionA radioactive elements has a half life of 2500 yrs. In how many years will its mass decay by 90% of its initial mass?
View SolutionThe half life of radioactive Radon is `3.8 days` . The time at the end of which `(1)/(20) th` of the radon sample will remain undecayed is `(given log e = 0.4343 ) `
View SolutionHalf life of a sample is 20 minutes. In how much time will the acitivity of sample drop to `1//16` of its initial value?
View SolutionTwo nuclei P and Q have equal number of atoms at t=0. Their half lives are 3 hrs and 9 hrs respectively. Compare their rates of disintegration after 18 hours form the starts.
View SolutionThe half life of a given radioactive nuclide is 138.6 days. What is the mean life of this nuclide? After how much time will a given sample of this nuclide get reduced to only 12.5% of its initial value?
View SolutionThe decay constant for a radio nuclide, has a value of `1.386 day^(-1)`. After how much time will a given sample of this nuclide get reduced to only 6.25% of its present number ?
View SolutionThe half life of a radioactive substance is `5xx10^(3)`yrs. In how many years will its activity decay to 0.2 times its initial activity? Take `log_(10) 5=0.6990`.
View Solutionthe count rate from a radioactive sample falls from `4.0xx10^6`per second to `1.0xx10^6` per second in 20 hours.What will be the count rate 100 hours after the begnning ?
View SolutionA sample of radioactive material has an activity of `9xx10^(12)` Becquerel. The material has a half life of 80s. How long will it take for the activity to falls to `2xx10^(10)` Becquerel ?
View SolutionBiologically useful technetium nuclei (with atomic weight 99) have a half life of 6 hrs. A solution containing `10^(-12)` g of this is injected into the bladder of a patient. Find its activity in the beginning and after one hour.
View SolutionFor a given sample, the countring rate is `47.5alpha` particle per minute. After 5 times, the count is reduced to `27 alpha` particles per minute. Find the decay constant and half life of the sample.
View SolutionThe selling rate of a radioactive isotope is decided by its activity. What will be the second-hand rate of a oe month old `P^32``(t_(1//2)=14.3` days) source if it was originally purchased for 800 rupees?
View SolutionOne milligram of thorium emits `22alpha` particles per minute per unit solid angle. Calculate average life of thorium. Atomic weight of Thorium is 232.
View SolutionA radioactive sample contains 2.2 mg of pure `._6C^(11)` , which has a half life period of 1224s. Calculate (i) number of atoms present initially. (ii) the activity when `5 mu g` of the sample will be left.
View SolutionIn the case of thorium `(A = 232 and Z = 90)`, we obtain an isotope of lead `(A = 208 and Z = 82)` after some radiactive disintegrations. The number of `alpha` and `beta` particle emitted are respectively.
View Solution
Exercise questions and complete solutions for chapter ATOMS AND NUCLEI of PRADEEP PHYSICS (HINGLISH) of Class 12
All Exercises from PRADEEP Class 12 PHYSICS ATOMS AND NUCLEI
- (I) Conceptual Problems 1
- (I) Conceptual Problems 14
- (I) Conceptual Problems 16
- (I) Conceptual Problems 18
- (I) Conceptual Problems 21
- (I) Conceptual Problems 22
- (I) Conceptual Problems 23
- (I) Conceptual Problems 24
- (I) Conceptual Problems 27
- (I) Conceptual Problems 29
- (I) Conceptual Problems 5
- (I) Conceptual Problems 6
- (I) Conceptual Problems 8
- (I) Questions short 10
- (I) Questions short 12
- (I) Questions short 5
- (I) Questions short 6
- (I) Questions very short 10
- (I) Questions very short 14
- (I) Questions very short 16
- (I) Questions very short 17
- (I) Questions very short 26
- (I) Short Answer questions 1
- (II) multiple choice question 101
- (II) multiple choice question 88
- (II) very short answer 16
- (II) Questions short 18
- (II) Questions very short 30
- (II) Questions very short 35
- (II) Questions very short 36
- (II) Questions very short 40
- (II) Questions very short 43
- (III) Questions short 20
- (III) Questions short 21
- (III) Questions short 22
- (III) Questions short 23
- (III) Questions short 25
- (III) Questions short 26
- (III) Questions short 27
- (III) Questions short 28
- (III) Questions short 31
- (III) Questions very short 50
- (III) Questions very short 51
- (III) Questions very short 53
- (III) Questions very short 54
- (III) Questions very short 55
- (III) Questions very short 56
- (III) Questions very short 57
- (III) Questions very short 59
- Additional Exercise 1
- Additional Exercise question 4
- Additional Exercise question 6
- Assertion- Reason type question 12
- Assertion- Reason type question 6
- curiocity quetions 1
- curiocity quetions 2
- curiocity quetions 3
- Exercise
- Exercise question 2
- Fill in the blancks 10
- Fill in the blancks 3
- Fill in the blancks 7
- Fill in the blancks 9
- Fill in the blank 2
- Higher order Thinking skills 11
- Higher order Thinking skills 5
- Higher order Thinking skills 6
- Higher order Thinking skills 7
- Long question 11
- Long question 12
- Long question 13
- Long question 14
- Long question 15
- Long question 16
- Multiple choice questions 1
- Multiple choice questions 2
- Multiple choice questions 3
- Multiple choice questions 7
- NCERT Multiple choice (I) questions 1
- NCERT Multiple choice (I) questions 2
- NCERT Multiple choice (I) questions 3
- NCERT Multiple choice (I) questions 4
- NCERT Multiple choice (I) questions 5
- NCERT Multiple choice (I) questions 7
- NCERT Multiple choice (II) questions 10
- NCERT Multiple choice (II) questions 11
- NCERT Multiple choice (II) questions 12
- NCERT Multiple choice (II) questions 8
- NCERT Multiple choice (II) questions 9
- NCERT Multiple choice (II) questions 8
- NCERT Multiple choice (II) questions 9
- Questions Long 1
- Questions Long 10
- Questions Long 11
- Questions Long 12
- Questions Long 13
- Questions Long 17
- Questions Long 20
- Questions Long 21
- Questions Long 5
- Questions Long 7
- Questions Long 9
- Questions short 10
- Questions short 11
- Questions short 12
- Questions short 15
- Questions short 16
- Questions short 17
- Questions short 6
- Questions short 7
- Questions short 8
- Questions short 9
- Short Answer question 4
- Short question 6
- short question 7
- Short question 9
- Solved Examples
- Value Based Questions 1
- Value Based Questions 2
- Value Based Questions 3
- Value Based Questions 4
- Value Based Questions 5
- Value Based Questions 6
- Very short question 1
- very short question 2
- very short question 3
- Very short question 4
- Very short question 5