Complete Solutions to Solved Examples of chapter ATOMS AND NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMS AND NUCLEI |
| PRADEEP | Solved Examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In the original experiment, Geiger and Marsden calculated the distance of closest approach to the gold nucleus (Z=79)- of a 7.7MeV `alpha` particle before it comes momentarily to rest and reverses its direction. What is its value?
View SolutionA 4MeV alpha particle is scattered by `20^@`, when it approaches a gold nucleus. Calculate the impact parameter if Z for gold is 79.
View SolutionFind the wavelength of electron orbiting in the first excited state of hydrogen atom.
View SolutionCalculate the radius of the third Bohr orbit of hydrogen atom and the energy of electron in that orbit.
View SolutionIn hydrogen atom, wavelength of emitted photon will be minimum in which of the following transitions?
(i) `n = 2` to `n = 1` , (ii) `n=6` to `n = 5` , (iii) `n = 3` to `n =2`
View SolutionCalculate the longest and shortest wavelength in the Balmer series of hydrogen atom. Given Rydberg constant =`1.0987xx10^7m^-1`.
View SolutionThe velocity of electron in inner most orbit of hydrogen atom is `2.2xx10^6 m//s`. Use de-Broglie hypothesis to calculate radius of innermost orbit.
View SolutionCalculate radius of first orbit of singly ionized He atom, when radius of first orbit of hydrogen atom is 0.53Å.
View SolutionThe energy of electron in 1st orbit of hydrogen atom is `-13.6 eV`. What will be the energy of doubly ionised `._(3)Li^(7)` atom in the first orbit?
View SolutionWhat are the numbers of protons and neutrons in the nucleus of `._92U^(238)`?
View SolutionObtain approximately the ratio of nuclear radii of `._26U^(56)` and `._92U^(238)`. What is the approximately ratio of their nuclear densities?
View SolutionExpress 150 microgram mass into equivalent energy in electron volt.
View SolutionCalculate mass defect, binding energy and binding energy per nucleon for a lithium nucleus `(._3Li^7)` taking its mass =7.000000a.m.u. Mass proton=1.007825 a.m.u. and mass of neutron =1.008665 a.m.u. Take 1a.m.u. =931.5 MeV.
View SolutionFind the half life of `U^(238)`, if one gram of it emits `1.24xx10^4` `alpha`-particle per second. Avogadro's Number `=6.023xx10^(23)`.
View SolutionThe half life of Radon is 3.8 days. Calculate how much of 15 milligram of Redon will remain after 38 days.
View SolutionHalf life on `Rn^(220)` is 55.5s. Calculate decay constant of this element.
View SolutionA radioactive isotope X has a half life of 3 seconds. At t=0, a given sample of this isotope contains 8000atom. Calculate (i) its decay constant (ii) average time (iii) the time `t_1`, when 1000 atoms of the isotope X remain in the sample (iv) number of decay/sec in the sample at `t=t_1sec.`
View SolutionA radioactive element decays to `1//32th` of its initial activity in 25 decay. Calculate its half life.
View SolutionAfter a series of alpha and beta decays, `._94Pu^(239)` becomes `._82Pb^(207)`. How many alpha and beta particles are emitted in the complete decay process?
View SolutionThe energy released in a nuclear fission process is `4.5xx10^(11)J`. Where in total mass involved is one gram. Calculate the percentage of mass defect in the process.
View SolutionThe mass defect in a nuclear fusion reaction is 0.3%. What amount of energy will be liberted in one kg fusion reaction.
View SolutionWhat is the distance of closest approach when a `5.0 MeV` proton approaches a gold nucleus?
View SolutionIn a Geiger Marsden experiment, calculate the distance of closest approach to the nucleus of Z=80, when an `alpha`-particle of `8 MeV` energy impings om it before it comes momentarily to rest and reverses its direction.
View SolutionCalculate the impact parameter of a 5MeV alpha particle scatterd by `10^@` when it approaches a gold nucleus. Take Z=79 for gold.
View SolutionIn a Geiger-Marsden experiment, calculate energy of `alpha` particle whose distance of closet approach to the nucleus of Z=79 is `2.8 xx 10^(-14)` m. How will the distance of closet approach be affected when the kinetic energy of the `alpha`-particle is doubled ?
View SolutionIn the original experiment, Geiger and Marsden calculated the distance of closest approach to the gold nucleus (Z=79)- of a 7.7MeV `alpha` particle before it comes momentarily to rest and reverses its direction. What is its value?
View SolutionIn a head on collision between an alpha particle and gold nucleus (Z=79), the distance of closest approach is 39.5 fermi. Calculate the energy of `alpha`-particle.
View SolutionWhat is the size of nucleus with Z=29 when an alpha particle of 12.5MeV kinetic energy retrace its path on colliding with the nucleus?
View SolutionCalculate the change in angular momentum of electron, when it jumps form 4th orbit to first orbit.
View SolutionThe energy of electron in hydrogen atom is `E_n=(-13.6)/(n^(2)) eV`, Where n=1, 2,3,......Show that (i) the electron in hydrogen atom cannot have an energy of -6.8eV. (ii) spacing between the lines (consecutive energy levels) within the given set of observed hydrogen spectrum decreases as n increases.
View SolutionThe energy level diagram of an element is given here. Which transition corresponds to the emission of a spectral line of wavelength 102.7nm?
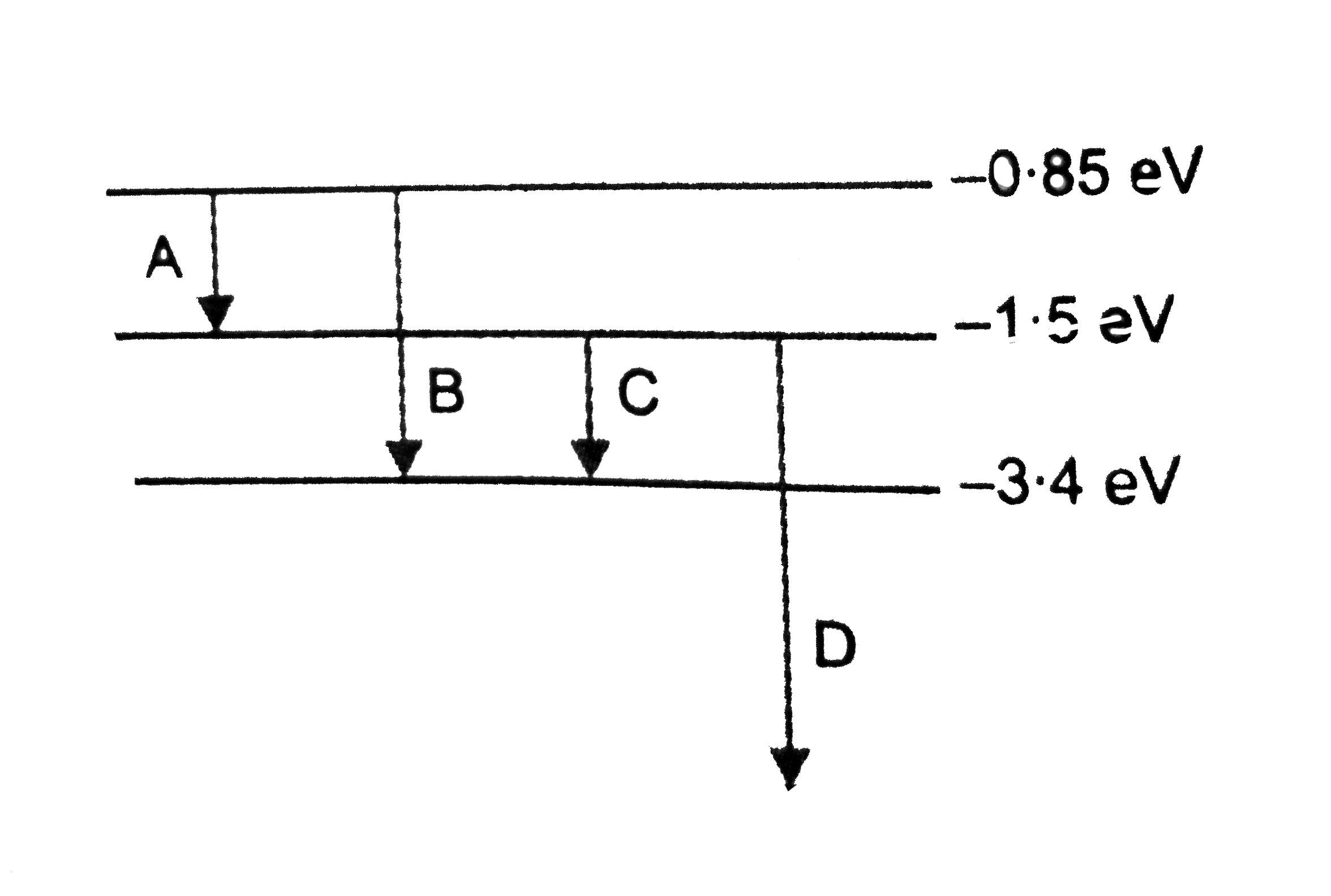
View SolutionIn the ground state of hydrogen atom, its Bohr radius is `5.3xx10^(-11)m`. The atom is excited such that the radius becomes `21.2xx10^(-11)m`. Find the value of principal quantum number and total energy of the atom in excited state.
View SolutionIn Rutherford's nuclear model of the atom, the nucleus (radius about `10^(-15)m`) is analogous to the sum about which the electron moves in orbit (radius about `10^(-10)m`) like the earth orbits around the sun. If the dimensions of the solar system had the same proportions as those of the atom, would the earth be closer to or further away form the sun than actually it is ? The radius of earth's orbit is about is `1.5xx10^(11)m`. The radius of the sun is taken as `7xx10^8m`.
View SolutionCalculate the value of Rydberg's constant.
View SolutionIt is found expertimentally that 13.6eV energy is required to separated a hydrogen atom into a proton and an electron. Compute the orbital radius and velocity of electron in a hydrogen atom.
View SolutionAccording to classical electromagnetic theory, calculate the initial frequency of the light emitted by the electron revolving around a proton in hydrogen atom.
View SolutionA 10kg satellite circles earth once every 2hr in an orbit having a radius of 8000km. Assuming that Bohr's angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, find the quantum number of the orbit of the satellite.
View SolutionUsing the Rydberg formula, calculate the wavelength of the first four spectral lines in the Lyman series of the hydrogen spectrum.
View SolutionFind the wavelength of `H_(alpha)` line given the value of Rydberg constant, `R=1.1xx10^7m^-1`.
View SolutionUsing Bohr's formula for energy quantization, determine (i) the longest wavelength in Lymann series of hydrogen atom spectrum. (ii) the excitation energy of the n=3 level of `He^(+)` atom. (iii) the ionization potential of the ground state of `Li^(++)` atom.
View SolutionCalculate the frequency of revolution of electron in the first Bohr orbit of hydrogen atom, if radius of first Bohr orbit is 0.5Å and velocity of electron in the first orbit is `2.24xx10^6m//s`.
View SolutionThe total energy of an electron in second excited state of hydrogen atom is -1.51eV. Calculate (i) KE of electron (ii) PE of electron in this state.
View SolutionWhich level of the doubly ionized lithium has the same energy as the ground state energy of the hydrogen atom? Compare the orbital radii of the two levels.
View SolutionWhich state of the triply ionized `Be^(+++)` has the same orbital radius as that of the ground state of hydrogen? Compare the energies of two states.
View SolutionThe ground state energy of hydrogen atom is -13.6eV. If an electron makes a transition form an energy level -0.85 eV to -3.4 eV, calculate the wavelength of spectral line emitted. To which series of hydrogen spectrum does this wavelength belongs?
View SolutionA 12.9 eV beam of electrons is used to bombard gaseous hydrogen atom at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelength of the first member of Paschen series and first member of Balmer series.
View SolutionA 12.5 eV electron beam is used to excite a gaseous hydrogen atom at room temperature. Determine the wavelengths and the corresponding series of the lines emitted.
View SolutionShow that the shortest wavelength lines in Lyman,Balmer and Paschen series have their wavelength in the ratio 1:4:9.
View SolutionA projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach `r_0`.
View Solutionfor scattering by an inverse square law field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle `theta` is given by
`b=(Ze^2 cot theta//2)/(4pi in_0(1/2mv^2))`
(a) What is the scattering angle for b=0?
(b) for given impact parameter, b, does the angle of deflection increase or decrease with increase in energy?
(c) What is the impact parameter at which the scattering angle is `90^@` for Z=79 and initial energy=10MeV?
(d) Why is it that the mass of the nucleus does not enter the formula above, but its charge does?
(e) for a given energy of the projectile, does the scattering angle increase or decrease with decrease in impact parameter?
View SolutionA 12.09 eV electron beam is used to bombard gaseous hydrogen at room temperature, Upto which energy level, the hydrogen atoms would be excited? Calculate the wavelengths of the second member of Lyman series and second member of Balmer series.
View SolutionThe nuclear mass of `._26F^(56)` is 55.85u. Calculate its nuclear density.
View SolutionThe natural boron is composed of two isotopes `._5beta^10` and `._5beta^11` having masses `10.003 u` and `11.009 u` resp. Find the relative abudance of each isotope in the natural boron if atomic mass of natural boron is 10.81u.
View SolutionCalculate number of protons and neutrons in `._92U^(235)` and the isotope `._88Ra^(236)`.
View SolutionExpress 1 joule in eV. Taking 1a.m.u. `=931 MeV`, calculate the mass of `._6C^12`.
View SolutionThe nuclear mass of `._26F^(56)` is 55.85u. Calculate its nuclear density.
View SolutionFind the effective mass of a photon if the wavelength of radiation is `3000Å`.
View SolutionCalculate the nuclear mass density of `._92U^(238)`. Given `R_0=1.5` fermi and mass of each nucleon is `1.67xx10^(-27)kg`.
View SolutionThe radius of `._3Al^(27)` nucleus is 5 fermi. Find the radius of `._52Te^(125)` nucleus.
View SolutionExpress 1 joule in eV. Taking 1a.m.u. `=931 MeV`, calculate the mass of `._6C^12`.
View SolutionCalculate the binding energy per nucleon of `._26Fe^(56)` nucleus. Given that mass of `._26Fe^(56)=55.934939u`, mass of proton `=1.007825u` and mass of neutron `=1.008665 u` and `1u=931MeV`.
View SolutionCalculate the B.E./nucleon of `._17Cl^(35)` nucleus. Given that of proton `=1.007825u`, mass of neutron `=1.008665 u`, mass of `._17Cl^(35)=34.980000u , 1u=931MeV`.
View SolutionCalculate the binding energy per nucleon of `._20Ca^(40)` nucleus. Given m `._20Ca^(40)=39.962589u` , `M_(p) =1.007825u` and `M_(n)=1.008665 u` and Take `1u=931MeV`.
View SolutionCalculate the energy equivalent of 1g of substance.
View SolutionFind the energy equivalent of one atomic mass unit, first in joule and then in MeV. Using this, express the mass defect of `._8O^(16)` in Me`V//c^2`. Given `M_(p)=1.007825u` and `M_(n) =1.008665 u, m_("oxy")=15.99053` a.m.u. and Take `1 a.m.u=933.75MeV//c^2`.
View SolutionCalculate binding energy per nucleon of `._83Bi^(209)`. Given that m `(._83Bi^(209))=208.980388am u`
`m("neutron") = 1.008665 am u`
`m ("proton") = 1.007825 am u`
View SolutionFind mass defect, binding energy and BE/nucleon for He nuclei. Take mass of He nucleus `=4.001509u`, `M_p = 1.007825u` and `M_n = 1.008665 u`
View SolutionFind the minimum energy required to separated a neutron form `._18Ar^(40)`. Given `M_n=1.008665 u` , mass of `._18Ar^(40)=39.962383u` and mass of `._18Ar^(39)=38.964314u`.
View SolutionThe decay constant for a given radioactive sample is 0.3465 `day^-1`. What percentage of this sample will get decayed in a period of 4 days?
View SolutionThe half life of radium is 1500 years. After how many years will one gram of pure radium
(i) reduce to 1 centigram?
(ii) lose one milligram?
View SolutionA radio active substance has a half life period of 30 days. Calculate (i) time taken for `3//4` of original number of atoms to disintegrate, (ii) time taken for `1//8` of the original number of atoms to remain unchanged.
View SolutionTritium has a half life of 12.5 years against beta decay. What fraction of a sample of pure tritium will remain undecayed after 25 years?
View SolutionA hypothetica atom has energy levels uniformaly separated by 1.3 eV. At a temperature 2500k, what is the ratio of number of atoms in 15th excited state to the number in 13 th excited state.
View SolutionIt is observed that only 6.25% of a given radioactive sample is left undecayed after a period of 16 days. What is the decay constant of this sample in `day^-1`?
View SolutionA radioactive material is reduced to `1/16` of its original amount in 4 days. How much material should one being with so that `4xx10^-3kg` of the material is left over after 6 days ?
View SolutionThe half life of radium is 1600 years. In how many years will one gram of pure radium be reduce to one centigram?
View SolutionHow many disintegrations per second will occur in one gram of `._92U^(238)`, if its half life against alpha decay is `1.42xx10^(17)s` ?
View SolutionThere are `4sqrt2xx10^6` radioactive nuclei in a given radioactive sample. If half life of sample is 20s, how many nuclei will decay in 10seconds?
View SolutionThe half life of `._92U^(238)` against `alpha` decay is `1.5xx10^(17)s`. What is the activity of the sample of `._92U^(238)` having `2.5xx10^(21)` atom?
View SolutionA radioactive sample contains 2.2 mg of pure `._6C^(11)` , which has a life period of 1224s. Calculate (i) number of atoms present initially. (ii) the activity when `5 mu g` of the sample will be left.
View SolutionThe half life of `._92C^(238)` against `alpha` -decay is `4.5xx10^9` years. What is the activity of 1g sample of `._92C^(238)`?
View SolutionDetermine the amount of `._84Po^(210)` necessary to provide a source of `alpha` particles of 5 millicurie strength. The half life of Po is 138 days.
View SolutionBiologically useful technetium nuclei (with atomic weight 99) have a half life of 6 hrs. A solution containing `10^(-12)` g of this is injected into the bladder of a patient. Find its activity in the beginning and after one hour.
View SolutionThe sequence of decay of radioactive nucleus is `D overset alphato D_1oversetbeta toD_2 oversetalpha toD_3`. If nucleon number and atomic number of `D_2` are 176 and 71 respectively, what are their values for D and `D_3`?
View Solution`._86Rn^(222)` is converted into `._84Po^(218)` and `._93Np^(239)` is converted into `._94Pu^(239)`. Name the particles emitted in each case and write down the corresponding equations.
View SolutionOne Mev positron encounters one MeV electron travelling in opposite direction. What is the wavelength travelling in opposite direction. What is the wavelength of photons produced, given rest mass energy of electron or positron `=0.512MeV` ? Take `h=6.62xx10^(-34)J-s`.
View SolutionComplete the decay reaction `._10Ne^(23) to?+._-1e^0+?`
Also, find the maximum KE of electrons emitted during this decay. Given mass of `._10Ne^(23)=22.994465 u`. mass of `._11Na^(23)=22.989768u`.
View SolutionThe atomic mass of uranium `._(92)^(238)U` is `23.058 u`, that of throium` ._(90)^(234)Th` is `234.0436 u` and that of an alpha particle `._2^4He` is `4.006 u`, Determine the energy released when `alpha-decay` converts`._(92)^(238)U` into `._(92)^(238) U`. int `._(90)^(234)Th`.
View SolutionA neutron is absorbed by a `._3Li^6` nucleus with subsequent emission of an alpha particle. Write the corresponding nuclear reaction. Calculate the energy released in this reaction.
`m(._3Li^6)=6.015126u, m(._2He^4)=4.0026044u`
`m(._0n^1)=1.0086654u, m(._1He^3)=3.016049u`
Take `1u=931MeV`.
View SolutionThe bombardment of Lithium with protons gives rise to the following reaction: `._3Li^7+._1H^1 to .2_He^4+.2_He^4+Q`
The atomic masses of lithium, hydrogen and helium are : `7.016u, 1.008u` and `4.004u` resp. Find the initial energy of each of `alpha` particle. Take `1a.m.u=931MeV`.
View SolutionFind the kinetic energy of the `alpha` - particle emitted in the decay `^238 Pu rarr ^234 U + alpha`. The atomic masses needed are as following:
`^238 Pu 238.04955 u`
`^234 U 234.04095 u`
`^4 He 4.002603 u`.
Neglect any recoil of the residual nucleus.
View SolutionWe are given the following atomic masses:
`._92Pu^(238)=238.05079u,`
`._90Th^(234)=234.04363u`,
`._91Pa^(237)=237.05121, ._1H^1=1.00783`,
`._2He^2=4.00260u`
(a) Calculate the energy released during `alpha` decay of `._92U^(238)`,
(b) Calculate the kinetic energy of emitted `alpha` particles,
(c) show that `._94Pu^(238)` cannot spontaneously emit a proton.
View SolutionConsider the beta decay
`^198 Au rarr ^198 Hg ** + Beta^(-1) + vec v`.
where `^198 Hg^**` represents a mercury nucleus in an excited state at energy `1.088 MeV` above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of `^198 Au` is `197.968233 u` and that of `^198 Hg` is `197.966760 u`.
View SolutionA neutron is absorbed by a `._3Li^6` nucleus with subsequent emission of an alpha particle. Write the corresponding nuclear reaction. Calculate the energy released in this reaction.
`m(._3Li^6)=6.015126u, m(._2He^4)=4.0026044u`
`m(._0n^1)=1.0086654u, m(._1He^3)=3.016049u`
Take `1u=931MeV`.
View SolutionIt is estimated that the atomic bomb exploded at Hiroshima released a total energy of `7.6xx10^(13)J`. If on the average, 200MeV energy was released per fission, calculate
(i) the number of Uranium atoms fissioned,
(ii) the mass of Uranium used in the bomb.
View SolutionCalculate the energy released when three alpha particles combine to form a `^12 C` nucleus. The atomic mass of `_2^4 He` is `4.002603 u`.
View SolutionThe energy released by fission of one `U^(235)` atom is 200 MeV. Calculate the energy released in kWh, when one gram of uranium undergoes fission.
View SolutionThe mass defect in a nuclear fusion reaction is 0.3%. What amount of energy will be liberated in one kg fusion reaction.
View SolutionIf `200 MeV` energy is released in the fission of a single `U^235` nucleus, the number of fissions required per second to produce `1` kilowatt power shall be (Given `1 eV = 1.6 xx 10^-19 J`).
View SolutionIn an experiment, the activity of 1.2 mg of radioactive potassium chloride (chloride of isotope of K-40) was found to be `170s^-1`: Taking molar mass to be `0.075 kg "mole"^-1` find the number of `K-40` atoms in the same and hence find the half life of `K-40`. Avogadro's number `=6.0xx10^(23)"mole"^-1`
View Solution
Solved Examples questions and complete solutions for chapter ATOMS AND NUCLEI of PRADEEP PHYSICS (HINGLISH) of Class 12
All Exercises from PRADEEP Class 12 PHYSICS ATOMS AND NUCLEI
- (I) Conceptual Problems 1
- (I) Conceptual Problems 14
- (I) Conceptual Problems 16
- (I) Conceptual Problems 18
- (I) Conceptual Problems 21
- (I) Conceptual Problems 22
- (I) Conceptual Problems 23
- (I) Conceptual Problems 24
- (I) Conceptual Problems 27
- (I) Conceptual Problems 29
- (I) Conceptual Problems 5
- (I) Conceptual Problems 6
- (I) Conceptual Problems 8
- (I) Questions short 10
- (I) Questions short 12
- (I) Questions short 5
- (I) Questions short 6
- (I) Questions very short 10
- (I) Questions very short 14
- (I) Questions very short 16
- (I) Questions very short 17
- (I) Questions very short 26
- (I) Short Answer questions 1
- (II) multiple choice question 101
- (II) multiple choice question 88
- (II) very short answer 16
- (II) Questions short 18
- (II) Questions very short 30
- (II) Questions very short 35
- (II) Questions very short 36
- (II) Questions very short 40
- (II) Questions very short 43
- (III) Questions short 20
- (III) Questions short 21
- (III) Questions short 22
- (III) Questions short 23
- (III) Questions short 25
- (III) Questions short 26
- (III) Questions short 27
- (III) Questions short 28
- (III) Questions short 31
- (III) Questions very short 50
- (III) Questions very short 51
- (III) Questions very short 53
- (III) Questions very short 54
- (III) Questions very short 55
- (III) Questions very short 56
- (III) Questions very short 57
- (III) Questions very short 59
- Additional Exercise 1
- Additional Exercise question 4
- Additional Exercise question 6
- Assertion- Reason type question 12
- Assertion- Reason type question 6
- curiocity quetions 1
- curiocity quetions 2
- curiocity quetions 3
- Exercise
- Exercise question 2
- Fill in the blancks 10
- Fill in the blancks 3
- Fill in the blancks 7
- Fill in the blancks 9
- Fill in the blank 2
- Higher order Thinking skills 11
- Higher order Thinking skills 5
- Higher order Thinking skills 6
- Higher order Thinking skills 7
- Long question 11
- Long question 12
- Long question 13
- Long question 14
- Long question 15
- Long question 16
- Multiple choice questions 1
- Multiple choice questions 2
- Multiple choice questions 3
- Multiple choice questions 7
- NCERT Multiple choice (I) questions 1
- NCERT Multiple choice (I) questions 2
- NCERT Multiple choice (I) questions 3
- NCERT Multiple choice (I) questions 4
- NCERT Multiple choice (I) questions 5
- NCERT Multiple choice (I) questions 7
- NCERT Multiple choice (II) questions 10
- NCERT Multiple choice (II) questions 11
- NCERT Multiple choice (II) questions 12
- NCERT Multiple choice (II) questions 8
- NCERT Multiple choice (II) questions 9
- NCERT Multiple choice (II) questions 8
- NCERT Multiple choice (II) questions 9
- Questions Long 1
- Questions Long 10
- Questions Long 11
- Questions Long 12
- Questions Long 13
- Questions Long 17
- Questions Long 20
- Questions Long 21
- Questions Long 5
- Questions Long 7
- Questions Long 9
- Questions short 10
- Questions short 11
- Questions short 12
- Questions short 15
- Questions short 16
- Questions short 17
- Questions short 6
- Questions short 7
- Questions short 8
- Questions short 9
- Short Answer question 4
- Short question 6
- short question 7
- Short question 9
- Solved Examples
- Value Based Questions 1
- Value Based Questions 2
- Value Based Questions 3
- Value Based Questions 4
- Value Based Questions 5
- Value Based Questions 6
- Very short question 1
- very short question 2
- very short question 3
- Very short question 4
- Very short question 5