Complete Solutions to Exercise of chapter ਸੰਭਾਵਨਾ of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | ਸੰਭਾਵਨਾ |
| PSEB (PUNJABI MEDIUM) | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
ਜਕਰ E ਅਤੇ F ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਘਟਨਾਵਾਂ ਹਨ ਕਿ `P(E) = 0.6, P(F) = 0.3` ਅਤੇ `P(E cap F) = 0.2` ਹੈ, ਤਾਂ `P(E|F)` ਅਤੇ `P(F|E)` ਪਤਾ ਕਰੋ।
02:34View Solution`P(A|B)` ਪਤਾ ਕਰੋ, ਜੇਕਰ `P(B) = 0.5` ਅਤੇ `P (A cap B) = 0.32` ਹੋਵੇ।
01:16View Solutionਜੇਕਰ `P(A) = 0.8, P(B) = 0.5` ਅਤੇ `P (B|A) = 0.4` ਪਤਾ ਕਰੋ। `P(AcapB)`
01:27View Solutionਜੇਕਰ `P(A) = 0.8, P(B) = 0.5` ਅਤੇ `P (B|A) = 0.4` ਪਤਾ ਕਰੋ। `P(A|B)`
01:59View Solutionਜੇਕਰ `P(A) = 0.8, P(B) = 0.5` ਅਤੇ `P (B|A) = 0.4` ਪਤਾ ਕਰੋ। `P(AcupB)`
02:10View Solution`P(A cup B)` ਪਤਾ ਕਰੋ, ਜੇਕਰ `P(A) = P(B) = 5/ 13` ਅਤੇ `P(A|B) = 2/ 5`
02:00View Solutionਜੇਕਰ `P(A) = 6/11 , P(B) = 5/11` ਅਤੇ `P(A Cup B) = 7/11` ਤਾਂ ਪਤਾ ਕਰੋ : `P(AcapB)`
01:30View Solutionਜੇਕਰ `P(A) = 6/11 , P(B) = 5/11` ਅਤੇ `P(A Cup B) = 7/11` ਤਾਂ ਪਤਾ ਕਰੋ : `P(A|B)`
02:00View Solutionਜੇਕਰ `P(A) = 6/11 , P(B) = 5/11` ਅਤੇ `P(A Cup B) = 7/11` ਤਾਂ ਪਤਾ ਕਰੋ : `P(B|A)`
01:56View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਇੱਕ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾਰ ਉਛਾਲਿਆ ਗਿਆ: E : ਤੀਜੀ ਉਛਾਲ ਤੇ ਚਿੱਤ, F : ਪਹਿਲੀ ਦੋਵੇਂ ਉਛਾਲਾਂ ਤੇ ਚਿੱਤ
03:33View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਇੱਕ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾਰ ਉਛਾਲਿਆ ਗਿਆ: E : ਘੱਟੋ-ਘੱਟ ਦੋ ਚਿੱਤ, F : ਵੱਧ ਤੋਂ ਵੱਧ ਇੱਕ ਚਿੱਤ
03:40View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਇੱਕ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾਰ ਉਛਾਲਿਆ ਗਿਆ: E : ਵੱਧ ਤੋਂ ਵੱਧ ਦੋ ਪਟ, F : ਘੱਟੋ-ਘੱਟ ਦੋ ਪਟ
03:23View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਦੋ ਸਿੱਕਿਆਂ ਨੂੰ ਇੱਕ ਵਾਰੀ ਉਛਾਲਿਆ ਗਿਆ : E : ਇੱਕ ਸਿੱਕੇ ਤੇ ਪਟ ਆਉਣਾ F : ਇੱਕ ਸਿੱਕੇ ਤੇ ਚਿੱਤ ਆਉਣਾ
02:31View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਦੋ ਸਿੱਕਿਆਂ ਨੂੰ ਇੱਕ ਵਾਰੀ ਉਛਾਲਿਆ ਗਿਆ : E : ਕੋਈ ਪਟ ਨਾ ਆਉਣਾ। F: ਕੋਈ ਚਿੱਤ ਨਾ ਆਉਣਾ
02:09View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਇੱਕ ਪਾਸੇ ਨੂੰ ਤਿੰਨ ਵਾਰੀ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ: E : ਤੀਜੀ ਉਛਾਲ ਤੇ ਸੰਖਿਆ 4 ਆਉਣਾ F : ਪਹਿਲੀ ਦੋ ਉਛਾਲਾਂ ਤੇ ਕ੍ਰਮਵਾਰ 6 ਅਤੇ 5 ਆਉਣਾ
05:08View Solution`P(E|F)` ਪਤਾ ਕਰੋ ਜੇਕਰ: ਇੱਕ ਪਰਿਵਾਰ ਦੇ ਚਿੱਤਰ ਵਿੱਚ ਮਾਤਾ, ਪਿਤਾ ਅਤੇ ਪੁੱਤਰ ਬੇਤਰਤੀਬੀ ਨਾਲ ਖੜੇ ਹਨ: E : ਪੁੱਤਰ ਇੱਕ ਸਿਰੇ ਤੇ ਖੜਾ ਹੈ, F : ਪਿਤਾ ਵਿਚਕਾਰ ਖੜਾ ਹੈ।
03:28View Solutionਇੱਕ ਕਾਲੇ ਅਤੇ ਇੱਕ ਲਾਲ ਪਾਸੇ ਨੂੰ ਉਛਾਲਿਆ ਗਿਆ ਹੈ : ਪਾਸਿਆਂ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ 9 ਹੋਣ ਦੀ ਬਾਸ਼ਰਤ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਜੇਕਰ ਇਹ ਪਤਾ ਹੋਵੇ ਕਿ ਕਾਲੇ ਪਾਸੇ ਤੇ 5 ਆਇਆ ਹੈ।
03:50View Solutionਇੱਕ ਕਾਲੇ ਅਤੇ ਇੱਕ ਲਾਲ ਪਾਸੇ ਨੂੰ ਉਛਾਲਿਆ ਗਿਆ ਹੈ : ਪਾਸਿਆਂ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ 8 ਹੋਣ ਦੀ ਬਾਸ਼ਰਤ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਜੇਕਰ ਇਹ ਪਤਾ ਹੋਵੇ ਕਿ ਲਾਲ ਪਾਸੇ ਤੇ ਸੰਖਿਆ 4 ਤੋਂ ਘੱਟ ਹੈ।
04:16View Solutionਇੱਕ ਨਿਰਪੱਖ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ। ਘਟਨਾਵਾਂ `E = {1,3,5}, F = {2,3}`, ਅਤੇ `G = {2,3,4,5}` ਲਈ ਪਤਾ ਕਰੋ : `P (E|F)` ਅਤੇ `P (F|E)`
03:21View Solutionਇੱਕ ਨਿਰਪੱਖ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ। ਘਟਨਾਵਾਂ `E = {1,3,5}, F = {2,3}`, ਅਤੇ `G = {2,3,4,5}` ਲਈ ਪਤਾ ਕਰੋ : `P (E|G)` ਅਤੇ `P(G|E)`
03:10View Solutionਇੱਕ ਨਿਰਪੱਖ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ। ਘਟਨਾਵਾਂ `E = {1,3,5}, F = {2,3}`, ਅਤੇ `G = {2,3,4,5}` ਲਈ ਪਤਾ ਕਰੋ : `P(EcupF|G)` ਅਤੇ `P(EcapF|G)`
04:41View Solutionਮੰਨ ਲਉ ਕਿ ਜਨਮ ਲੈਣ ਵਾਲੇ ਬੱਚੇ ਦਾ ਮੁੰਡਾ ਜਾਂ ਕੁੜੀ ਹੋਣਾ ਸਮ- ਸੰਭਾਵੀ ਹੈ। ਜੇਕਰ ਕਿਸੇ ਪਰਿਵਾਰ ਵਿੱਚ ਦੋ ਬੱਚੇ ਹਨ, ਤਾਂ ਦੋਵੇਂ ਬੱਚਿਆ ਦੇ ਕੁੜੀ ਹੋਣ ਦੀ ਬਾਸ਼ਰਤ ਸੰਭਾਵਨਾ ਕੀ ਹੈ, ਜੇਕਰ ਇਹ ਦਿੱਤਾ ਹੋਵੇ ਕਿ ਸਭ ਤੋਂ ਛੋਟਾ ਬੱਚਾ ਕੁੜੀ ਹੈ
02:46View Solutionਮੰਨ ਲਉ ਕਿ ਜਨਮ ਲੈਣ ਵਾਲੇ ਬੱਚੇ ਦਾ ਮੁੰਡਾ ਜਾਂ ਕੁੜੀ ਹੋਣਾ ਸਮ- ਸੰਭਾਵੀ ਹੈ। ਜੇਕਰ ਕਿਸੇ ਪਰਿਵਾਰ ਵਿੱਚ ਦੋ ਬੱਚੇ ਹਨ, ਤਾਂ ਦੋਵੇਂ ਬੱਚਿਆ ਦੇ ਕੁੜੀ ਹੋਣ ਦੀ ਬਾਸ਼ਰਤ ਸੰਭਾਵਨਾ ਕੀ ਹੈ, ਜੇਕਰ ਇਹ ਦਿੱਤਾ ਹੋਵੇ ਕਿ ਘੱਟੋ-ਘੱਟ ਇੱਕ ਬੱਚਾ ਕੁੜੀ ਹੈ।
02:38View Solutionਇੱਕ ਅਧਿਆਪਕ ਦੇ ਕੋਲ 300 ਸੱਚ/ਝੂਠ ਤਰ੍ਹਾਂ ਦੇ ਅਸਾਨ ਪ੍ਰਸ਼ਨ, 200 ਸੱਚ/ਝੂਠ ਤਰ੍ਹਾਂ ਦੇ ਮੁਸ਼ਕਿਲ ਪ੍ਰਸ਼ਨ, 500 ਬਹੁ- ਵਿਕਲਪ ਪ੍ਰਕਾਰ ਦੇ ਅਸਾਨ ਪ੍ਰਸ਼ਨ ਅਤੇ 400 ਬਹੁ- ਵਿਕਲਪ ਪ੍ਰਕਾਰ ਦੇ ਮੁਸ਼ਕਿਲ ਪ੍ਰਸ਼ਨ ਹਨ। ਜੇਕਰ ਪ੍ਰਸ਼ਨਾ ਵਿੱਚੋਂ ਇੱਕ ਪ੍ਰਸ਼ਨ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇੱਕ ਅਸਾਨ ਪ੍ਰਸ਼ਨ ਦੀ ਬਹੁ-ਵਿਕਲਪੀ ਹੋਣ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ?
04:21View Solutionਇਹ ਦਿੱਤਾ ਹੋਇਆ ਹੈ ਕਿ ਦੋ ਪਾਸਿਆਂ ਨੂੰ ਸੁੱਟਣ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆਵਾਂ ਵੱਖ- ਵੱਖ ਹਨ। ਦੋਵੇਂ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ 4 ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
04:17View Solutionਇੱਕ ਪਾਸੇ ਨੂੰ ਸੁੱਟਣ ਦੇ ਪ੍ਰਯੋਗ ਤੇ ਵਿਚਾਰ ਕਰੋ। ਜੇਕਰ ਪਾਸੇ ਤੇ ਆਈ ਸੰਖਿਆ 3 ਦੀ ਗੁਣਜ ਹੈ ਤਾਂ ਪਾਸੇ ਨੂੰ ਦੁਬਾਰਾ ਸੁੱਟੋ ਅਤੇ ਜੇਕਰ ਕੋਈ ਹੋਰ ਸੰਖਿਆ ਆਵੇ ਤਾਂ ਇੱਕ ਸਿੱਕੇ ਨੂੰ ਉਛਾਲੋ। ਘਟਨਾ ‘ਘੱਟੋ- ਘੱਟ ਇੱਕ ਪਾਸ਼ੇ ਤੇ ਸੰਖਿਆ 3 ਆਉਣਾ ’ ਦਿੱਤਾ ਹੋਇਆ ਹੈ ਤਾਂ ਘਟਨਾ ‘ਸਿੱਕੇ ਤੇ ਪੱਟ ਆਉਣਾ’ ਦੀ ਬਾਸ਼ਰਤ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
04:25View Solutionਜੇਕਰ `P (A) = 1/2 , P(B) = 0` ਤਾਂ `P (A|B)` ਹੈ :
01:06View Solutionਜੇਕਰ A ਅਤੇ B ਦੋ ਘਟਨਾਵਾਂ ਇਸ ਪ੍ਰਕਾਰ ਹਨ ਕਿ `P (A|B) = P(B|A) ne 0` ਤਾਂ:
01:38View Solutionਜੇਕਰ `P(A)=3/5, P(B) = 1/5` ਅਤੇ A ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਹਨ ਤਾਂ `P (A cap B)` ਪਤਾ ਕਰੋ।
01:45View Solution52 ਪੱਤਿਆਂ ਦੀ ਇੱਕ ਗੁੱਟੀ ਵਿੱਚੋਂ ਬੇਤਰਤੀਬੀ ਨਾਲ ਬਿਨਾਂ ਬਦਲੇ ਦੋ ਪੱਤੇ ਕੱਢੇ ਗਏ। ਦੋਵੇਂ ਪੱਤਿਆਂ ਦੇ ਕਾਲੇ ਰੰਗ ਦਾ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
02:01View Solutionਸੰਤਰਿਆਂ ਦੇ ਇੱਕੋਂ ਬਕਸੇ ਦਾ ਨਿਰੀਖਣ ਉਸ ਵਿੱਚੋਂ ਬੇਤਰਤੀਬੀ ਨਾਲ ਬਗੈਰ ਬਦਲੇ ਤਿੰਨ ਸੰਤਰੇ ਕੱਢ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਜੇਕਰ ਤਿੰਨੇ ਕੱਢੇ ਹੋਏ ਸੰਤਰੇ ਚੰਗੇ ਹੋਣ ਤਾਂ ਬਕਸੇ ਨੂੰ ਵੇਚਣ ਲਈ ਸਵੀਕਾਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਨਹੀਂ ਤਾਂ ਅਸਵੀਕਾਰ ਕਰ ਦਿੰਦੇ ਹਨ। ਇੱਕ ਬਕਸੇ, ਜਿਸ ਵਿੱਚ 15 ਸੰਤਰੇ ਹਨ ਜਿਹਨਾਂ ਵਿੱਚੋਂ 12 ਚੰਗੇ ਅਤੇ 3 ਖਰਾਬ ਸੰਤਰੇ ਹਨ, ਕੀ ਵਿਕਰੀ ਲਈ ਸਵੀਕਾਰ ਹੋਣ ਲਈ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
03:19View Solutionਇੱਕ ਨਿਰਪੱਖ ਸਿੱਕਾ ਅਤੇ ਇੱਕ ਨਿਰਪੱਖ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਗਿਆ। ਮੰਨ ਲਉ A ਘਟਨਾ ‘ ਸਿੱਕੇ ਤੇ ਚਿੱਤ ਆਉਣਾ’ ਅਤੇ B ਘਟਨਾ ‘ਪਾਸੇ ਤੇ ਸੰਖਿਆ 3 ਆਉਣਾ’ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ। ਨਿਰੀਖਣ ਕਰੋ ਕਿ ਘਟਨਾਵਾਂ A ਅਤੇ B ਅਜ਼ਾਦ ਹਨ ਜਾਂ ਨਹੀਂ?
03:38View Solutionਇੱਕ ਪਾਸੇ ਤੇ 1, 2, 3 ਲਾਲ ਰੰਗ ਨਾਲ ਅਤੇ 4, 5, 6 ਹਰੇ ਰੰਗ ਨਾਲ ਲਿਖੇ ਗਏ ਹਨ। ਇਸ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਗਿਆ। ਮੰਨ ਲਉ A ਘਟਨਾ 'ਸੰਖਿਆ ਜਿਸਤ ਹੈ’ ਅਤੇ B ਘਟਨਾ ‘ ਸੰਖਿਆ ਲਾਲ ਰੰਗ ਨਾਲ ਲਿਖੀ ਹੋਈ ਹੈ’, ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ। ਕੀ A ਅਤੇ B ਅਜ਼ਾਦ ਹਨ?
02:44View Solutionਮੰਨ ਲਉ E ਅਤੇ F ਦੋ ਘਟਨਾਵਾਂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ `P(E)=3/5, P(F)=3/10` ਅਤੇ `P (E cap F)=1/5` ਤਾਂ ਕੀ E ਅਤੇ F ਅਜ਼ਾਦ ਹਨ?
01:45View SolutionA ਅਤੇ B ਇਹੋ ਜਿਹੀ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ `P(A) = 1/2, P(AcupB)=3/5` ਅਤੇ `P(B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜੇਕਰ ਘਟਨਾਵਾਂ ਆਪਸ ਵਿੱਚ ਨਿਵੇਕਲੀਆਂ ਹਨ
02:19View SolutionA ਅਤੇ B ਇਹੋ ਜਿਹੀ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ `P(A) = 1/2, P(AcupB)=3/5` ਅਤੇ `P(B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜੇਕਰ ਘਟਨਾਵਾਂ ਅਜ਼ਾਦ ਹਨ।
02:46View Solutionਮੰਨ ਲਉ A ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਹਨ ਅਤੇ `P(A) = 0.3` ਅਤੇ `P(B) = 0.4` ਹੈ, ਤਾਂ ਪਤਾ ਕਰੋ: `P(AcapB)`
01:24View Solutionਮੰਨ ਲਉ A ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਹਨ ਅਤੇ `P(A) = 0.3` ਅਤੇ `P(B) = 0.4` ਹੈ, ਤਾਂ ਪਤਾ ਕਰੋ: `P(AcupB)`
02:08View Solutionਮੰਨ ਲਉ A ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਹਨ ਅਤੇ `P(A) = 0.3` ਅਤੇ `P(B) = 0.4` ਹੈ, ਤਾਂ ਪਤਾ ਕਰੋ: `P(A|B)`
02:10View Solutionਮੰਨ ਲਉ A ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਹਨ ਅਤੇ `P(A) = 0.3` ਅਤੇ `P(B) = 0.4` ਹੈ, ਤਾਂ ਪਤਾ ਕਰੋ: `P(B|A)`
02:00View Solutionਦਿੱਤੀ ਹੋਈ ਘਟਨਾਵਾਂ A ਅਤੇ B ਇਹੋ ਜਿਹੀਆਂ ਹਨ, ਜਿੱਥੇ `P(A)=1/4, P(B) =1/2` ਅਤੇ `P(Acap B) =1/8` ਤਾਂ `P(A ਨਹੀਂ ਅਤੇ B ਨਹੀਂ)` ਪਤਾ ਕਰੋ।
03:03View Solutionਮੰਨ ਲਉ A ਅਤੇ B ਇਹੋ ਜਿਹੀਆਂ ਘਟਨਾਵਾਂ ਹਨ ਕਿ `P(A) =1/2` ਅਤੇ `P(B) =7/12` ਅਤੇ `P(A` ਨਹੀਂ ਅਤੇ B ਨਹੀਂ)`=1/4` ਹੈ। ਕੀ A ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਹੈ?
04:50View SolutionA ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ `P(A) = 0.3`, ਅਤੇ `P(B) = 0.6` ਤਾਂ `P(A` ਅਤੇ B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ।
01:31View SolutionA ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ `P(A) = 0.3`, ਅਤੇ `P(B) = 0.6` ਤਾਂ P(A ਅਤੇ B ਨਹੀਂ) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ।
02:25View SolutionA ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ `P(A) = 0.3`, ਅਤੇ `P(B) = 0.6` ਤਾਂ P(A ਜਾਂ B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ।
02:05View SolutionA ਅਤੇ B ਅਜ਼ਾਦ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ `P(A) = 0.3`, ਅਤੇ `P(B) = 0.6` ਤਾਂ `P(A` ਅਤੇ B ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ।
03:29View Solutionਇੱਕ ਪਾਸੇ ਨੂੰ ਤਿੰਨ ਵਾਰੀ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਘੱਟੋ ਘੱਟ ਇੱਕ ਵਾਰੀ ਟਾਂਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
03:23View Solutionਦੋ ਗੇਂਦਾ ਇੱਕ ਡੱਬੇ ਵਿੱਚੋਂ ਬਿਨਾਂ ਬਦਲੇ ਕੱਢੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਡੱਬੇ ਵਿੱਚ 10 ਕਾਲੀਆਂ ਅਤੇ 8 ਲਾਲ ਗੇਂਦਾਂ ਹਨ ਤਾਂ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ ਦੋਵੇਂ ਗੇਂਦਾ ਲਾਲ ਹਨ।
02:11View Solutionਦੋ ਗੇਂਦਾ ਇੱਕ ਡੱਬੇ ਵਿੱਚੋਂ ਬਿਨਾਂ ਬਦਲੇ ਕੱਢੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਡੱਬੇ ਵਿੱਚ 10 ਕਾਲੀਆਂ ਅਤੇ 8 ਲਾਲ ਗੇਂਦਾਂ ਹਨ ਤਾਂ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ ਪਹਿਲੀ ਕਾਲੀ ਤੇ ਦੂਜੀ ਲਾਲ ਹੈ
01:57View Solutionਦੋ ਗੇਂਦਾ ਇੱਕ ਡੱਬੇ ਵਿੱਚੋਂ ਬਿਨਾਂ ਬਦਲੇ ਕੱਢੀਆਂ ਜਾਂਦੀਆਂ ਹਨ। ਡੱਬੇ ਵਿੱਚ 10 ਕਾਲੀਆਂ ਅਤੇ 8 ਲਾਲ ਗੇਂਦਾਂ ਹਨ ਤਾਂ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ ਇੱਕ ਕਾਲੀ ਅਤੇ ਦੂਜੀ ਲਾਲ ਹੈ।
02:54View Solutionਇੱਕ ਖਾਸ ਸਮੱਸਿਆ ਨੂੰ A ਅਤੇ B ਰਾਹੀਂ ਅਜ਼ਾਦੀ ਨਾਲ ਹੱਲ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾਵਾਂ ਕ੍ਰਮਵਾਰ `1/2` ਅਤੇ `1/3` ਹਨ। ਜੇਕਰ ਦੋਵੇਂ, ਅਜ਼ਾਦੀ ਨਾਲ ਸਮੱਸਿਆ ਹੱਲ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ, ਤਾਂ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ: ਸਮੱਸਿਆ ਹੱਲ ਹੋਵੇਗੀ।
02:31View Solutionਇੱਕ ਖਾਸ ਸਮੱਸਿਆ ਨੂੰ A ਅਤੇ B ਰਾਹੀਂ ਅਜ਼ਾਦੀ ਨਾਲ ਹੱਲ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾਵਾਂ ਕ੍ਰਮਵਾਰ `1/2` ਅਤੇ `1/3` ਹਨ। ਜੇਕਰ ਦੋਵੇਂ, ਅਜ਼ਾਦੀ ਨਾਲ ਸਮੱਸਿਆ ਹੱਲ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ, ਤਾਂ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ: ਉਹਨਾ ਵਿੱਚੋਂ ਕੇਵਲ ਇਹ ਇੱਕ ਹੱਲ ਕਰੇਗਾ।
03:11View Solutionਤਾਸ਼ ਦੇ 52 ਪੱਤਿਆਂ ਦੀ ਇੱਕ ਫੈਂਟੀ ਹੋਈ ਗੁੱਟੀ ਵਿੱਚੋਂ ਇੱਕ ਪੱਤਾ ਬੇਤਰਤੀਬੀ ਨਾਲ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ਹੇਠ ਲਿਖੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਹਾਲਤਾਂ ਵਿੱਚ ਘਟਨਾਵਾਂ E ਅਤੇ F ਅਜ਼ਾਦ ਹੈ? E : ‘ਕੱਢਿਆ ਹੋਇਆ ਪੱਤਾ ਹੁਕਮ ਦਾ ਹੈ। F : ‘ਕੱਢਿਆ ਹੋਇਆ ਪੱਤਾ ਇੱਕਾ ਹੈ।
03:25View Solutionਤਾਸ਼ ਦੇ 52 ਪੱਤਿਆਂ ਦੀ ਇੱਕ ਫੈਂਟੀ ਹੋਈ ਗੁੱਟੀ ਵਿੱਚੋਂ ਇੱਕ ਪੱਤਾ ਬੇਤਰਤੀਬੀ ਨਾਲ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ਹੇਠ ਲਿਖੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਹਾਲਤਾਂ ਵਿੱਚ ਘਟਨਾਵਾਂ E ਅਤੇ F ਅਜ਼ਾਦ ਹੈ? E : ‘ਕੱਢਿਆ ਹੋਇਆ ਪੱਤਾ ਕਾਲੇ ਰੰਗ ਦਾ ਹੈ। F : ‘ਕੱਢਿਆ ਹੋਇਆ ਪੱਤਾ ਬਾਦਸ਼ਾਹ ਹੈ।
03:02View Solutionਤਾਸ਼ ਦੇ 52 ਪੱਤਿਆਂ ਦੀ ਇੱਕ ਫੈਂਟੀ ਹੋਈ ਗੁੱਟੀ ਵਿੱਚੋਂ ਇੱਕ ਪੱਤਾ ਬੇਤਰਤੀਬੀ ਨਾਲ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ ਹੇਠ ਲਿਖੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਹਾਲਤਾਂ ਵਿੱਚ ਘਟਨਾਵਾਂ E ਅਤੇ F ਅਜ਼ਾਦ ਹੈ? E : ‘ਕੱਢਿਆ ਹੋਇਆ ਪੱਤਾ ਬਾਦਸ਼ਾਹ ਜਾਂ ਬੇਗਮ ਹੈ। F : ‘ਕੱਢਿਆ ਹੋਇਆ ਪੱਤਾ ਬੇਗਮ ਜਾਂ ਗੁਲਾਮ ਹੈ।
03:36View Solutionਇੱਕ ਹੋਸਟਲ ਵਿੱਚ 60% ਵਿਦਿਆਰਥੀ ਹਿੰਦੀ ਦਾ, 40% ਅੰਗਰੇਜ਼ੀ ਦਾ ਅਤੇ 20% ਦੋਵੇਂ ਭਾਸ਼ਾਵਾਂ ਦਾ ਅਖਬਾਰ ਪੜ੍ਹਦੇ ਹਨ। ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੂੰ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ। ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ ਉਹ ਨਾ ਤਾਂ ਹਿੰਦੀ ਅਤੇ ਨਾ ਹੀ ਅੰਗਰੇਜ਼ੀ ਦਾ ਅਖਬਾਰ ਪੜ੍ਹਦਾ ਹੈ।
03:49View Solutionਇੱਕ ਹੋਸਟਲ ਵਿੱਚ 60% ਵਿਦਿਆਰਥੀ ਹਿੰਦੀ ਦਾ, 40% ਅੰਗਰੇਜ਼ੀ ਦਾ ਅਤੇ 20% ਦੋਵੇਂ ਭਾਸ਼ਾਵਾਂ ਦਾ ਅਖਬਾਰ ਪੜ੍ਹਦੇ ਹਨ। ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੂੰ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ। ਜੇਕਰ ਉਹ ਹਿੰਦੀ ਦਾ ਅਖਬਾਰ ਪੜ੍ਹਦਾ ਹੈ ਤਾਂ ਉਸਦੇ ਅੰਗਰੇਜ਼ੀ ਦਾ ਅਖਬਾਰ ਵੀ ਪੜ੍ਹਨ ਵਾਲਾ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
02:20View Solutionਇੱਕ ਹੋਸਟਲ ਵਿੱਚ 60% ਵਿਦਿਆਰਥੀ ਹਿੰਦੀ ਦਾ, 40% ਅੰਗਰੇਜ਼ੀ ਦਾ ਅਤੇ 20% ਦੋਵੇਂ ਭਾਸ਼ਾਵਾਂ ਦਾ ਅਖਬਾਰ ਪੜ੍ਹਦੇ ਹਨ। ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੂੰ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ। ਜੇਕਰ ਉਹ ਅੰਗਰੇਜ਼ੀ ਦਾ ਅਖਬਾਰ ਪੜ੍ਹਦਾ ਹੈ ਤਾਂ ਉਸਦੇ ਹਿੰਦੀ ਦਾ ਅਖਬਾਰ ਵੀ ਪੜ੍ਹਨ ਵਾਲਾ, ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ।
02:46View Solutionਜੇਕਰ ਪਾਸਿਆਂ ਦਾ ਇੱਕ ਜੋੜਾ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਹਰੇਕ ਪਾਸੇ ਤੇ ਜਿਸਤ ਅਭਾਜ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕੀ ਹੈ?
02:55View Solutionਦੋ ਘਟਨਾਵਾਂ A ਅਤੇ B ਨੂੰ ਆਪਸ ਵਿੱਚ ਅਜ਼ਾਦ ਕਹਿੰਦੇ ਹਨ, ਜੇਕਰ
04:29View Solutionਇੱਕ ਕਲਸ਼ ਵਿੱਚ 5 ਲਾਲ ਅਤੇ 5 ਕਾਲੀਆਂ ਗੇਂਦਾ ਹਨ। ਬੇਤਰਤੀਬੀ ਨਾਲ ਇੱਕ ਗੇਂਦ ਕੱਢੀ ਜਾਂਦੀ ਹੈ, ਜਿਸਦਾ ਰੰਗ ਨੋਟ ਕਰਨ ਦੇ ਬਾਅਦ ਦੁਬਾਰਾ ਕਲਸ਼ ਵਿੱਚ ਪਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ। ਕੱਢੇ ਹੋਏ ਰੰਗ ਦੀਆਂ 2 ਹੋਰ ਗੇਂਦਾਂ ਕਲਸ਼ ਵਿੱਚ ਪਾ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਕਲਸ਼ ਵਿਚੋਂ ਇੱਕ ਗੇਂਦ ਕੱਢੀ ਜਾਂਦੀ ਹੈ। ਦੂਜੀ ਗੇਂਦ ਦੀ ਲਾਲ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ?
05:07View Solutionਇੱਕ ਥੈਲੇ ਵਿੱਚ 4 ਲਾਲ ਅਤੇ 4 ਕਾਲੀਆਂ ਗੇਂਦਾ ਹਨ ਅਤੇ ਥੈਲੇ ਵਿੱਚ 2 ਲਾਲ ਅਤੇ 6 ਕਾਲੀਆਂ ਗੇਂਦਾਂ ਹਨ। ਦੋਵੇਂ ਥੈਲਿਆਂ ਵਿੱਚੋਂ ਇੱਕ ਨੂੰ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਸ ਵਿੱਚੋਂ ਇੱਕ ਗੇਂਦ ਕੱਢੀ ਜਾਂਦੀ ਹੈ ਜਿਹੜੀ ਕਿ ਲਾਲ ਹੈ। ਇਸ ਗੱਲ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਗੇਂਦ ਪਹਿਲੇ ਥੈਲੇ ਵਿੱਚੋਂ ਕੱਢੀ ਹੈ?
04:28View Solutionਇਹ ਪਤਾ ਕਰੋ ਕਿ ਇੱਕ ਕਾਲਜ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਵਿੱਚੋਂ 60% ਹੋਸਟਲ ਵਿੱਚ ਰਹਿੰਦੇ ਹਨ ਅਤੇ 40% ਹੋਸਟਲ ਵਿੱਚ ਨਹੀਂ ਰਹਿੰਦੇ ਹਨ। ਪਹਿਲਾਂ ਦੇ ਸਾਲਾਂ ਦੇ ਨਤੀਜੇ ਸੂਚਿਤ ਕਰਦੇ ਹਨ ਕਿ ਹੋਸਟਲ ਵਿੱਚ ਰਹਿਣ ਵਾਲੇ ਵਿਦਿਆਰਥੀਆਂ ਵਿੱਚੋਂ 30% ਅਤੇ ਹੋਸਟਲ ਵਿੱਚ ਨਾ ਰਹਿਣ ਵਾਲੇ ਵਿਦਿਆਰਥੀਆਂ ਵਿੱਚੋਂ 20% ਵਿਦਿਆਰਥੀਆਂ ਨੇ A ਗਰੇਡ ਲਿਆ। ਸਾਲ ਦੇ ਅੰਤ ਵਿੱਚ ਕਾਲਜ ਦੇ ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੂੰ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਗਿਆ ਅਤੇ ਇਹ ਪਾਇਆ ਗਿਆ ਕਿ ਉਸਨੂੰ A-ਗਰੇਡ ਮਿਲਿਆ ਹੈ। ਇਸ ਗੱਲ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਉਹ ਵਿਦਿਆਰਥੀ ਹੋਸਟਲ ਵਿੱਚ ਰਹਿਣ ਵਾਲਾ ਹੈ?
05:28View Solutionਇੱਕ ਬਹੁ-ਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ ਦਾ ਉਤਰ ਦੇਣ ਵਿੱਚ ਇੱਕ ਵਿਦਿਆਰਥੀ ਜਾਂ ਤਾਂ ਪ੍ਰਸ਼ਨ ਦਾ ਉਤਰ ਜਾਣਦਾ ਹੈ ਜਾਂ ਉਹ ਅੰਦਾਜ਼ਾ ਲਗਾਉਂਦਾ ਹੈ। ਮੰਨ ਲਉ ਕਿ ਉਸਦੇ ਉਤਰ ਜਾਨਣ ਦੀ ਸੰਭਾਵਨਾ `3/4` ਹੈ ਅਤੇ ਅੰਦਾਜ਼ਾ ਲਗਾਉਣ ਦੀ ਸੰਭਾਵਨਾ `1/4` ਹੈ। ਮੰਨ ਲਉ ਕਿ ਵਿਦਿਆਰਥੀ ਦੇ ਪ੍ਰਸ਼ਨ ਦੇ ਉਤਰ ਦਾ ਅੰਦਾਜ਼ਾ ਲਗਾਉਣਤੇ ਸਹੀ ਉਤਰ ਦੇਣ ਦੀ ਸੰਭਾਵਨਾ `1/4` ਹੈ ਤਾਂ ਇਸ ਗੱਲ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਕੋਈ ਵਿਦਿਆਰਥੀ ਪ੍ਰਸ਼ਨ ਦਾ ਉਤਰ ਜਾਣਦਾ ਹੈ ਜੇਕਰ ਇਹ ਪਤਾ ਹੈ ਕਿ ਉਸਨੇ ਸਹੀ ਉਤਰ ਦਿੱਤਾ ਹੈ?
04:26View Solutionਕਿਸੇ ਖਾਸ ਰੋਗ ਦੇ ਸਹੀ ਪ੍ਰੀਖਿਅਣ ਲਈ ਖੂਨ ਦੀ ਜਾਂਚ 99% ਅਸਰਦਾਰ ਹੈ, ਜਦੋਂ ਅਸਲ ਵਿੱਚ ਰੋਗੀ ਉਸ ਰੋਗ ਤੋਂ ਪੀੜਿਤ ਹੈ। ਪਰ 0.5% ਵਾਰੀ ਕਿਸੇ ਠੀਕ ਵਿਅਕਤੀ ਦੇ ਖੂਨ ਦੀ ਜਾਂਚ ਕਰਨ ਤੇ ਪ੍ਰੀਖਿਅਣ ਗਲਤ ਰਿਪੋਰਟ ਦਿੰਦਾ ਹੈ ਭਾਵ ਵਿਅਕਤੀ ਨੂੰ ਰੋਗ ਤੋਂ ਪੀੜਿਤ ਦੱਸਦਾ ਹੈ। ਜੇਕਰ ਕਿਸੇ ਅਬਾਦੀ ਵਿੱਚ 0-1% ਲੋਗ ਉਸ ਰੋਗ ਤੋਂ ਪੀੜਿਤ ਹਨ ਤਾਂ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਕੋਈ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਹੋਇਆ ਵਿਅਕਤੀ ਉਸ ਰੋਗ ਤੋਂ ਪੀੜਿਤ ਹੋਵੇਗਾ ਜੇਕਰ ਉਸਦੇ ਖੂਨ ਦੀ ਜਾਂਚ ਵਿੱਚ ਦੱਸਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਉਸਨੂੰ ਇਹ ਰੋਗ ਹੈ?
06:45View Solutionਤਿੰਨ ਸਿੱਕੇ ਦਿੱਤੇ ਹਨ। ਇੱਕੇ ਸਿੱਕੇ ਦੇ ਦੋਵੇਂ ਪਾਸੇ ਚਿੱਤ ਹੈ। ਦੂਜਾ ਸਿੱਕਾ ਪੱਖਪਾਤੀ ਹੈ ਜਿਸ ਵਿੱਚ ਚਿੱਤ 75% ਵਾਰੀ ਆਉਂਦੀ ਹੈ ਅਤੇ ਤੀਜਾ ਸਿੱਕਾ ਨਿਰਪੱਖ ਹੈ। ਤਿੰਨਾਂ ਵਿੱਚੋਂ ਇੱਕ ਸਿੱਕਾ ਬੇਤਰਤੀਬੀ ਨਾਲ ਚੁਣਿਆ ਗਿਆ ਅਤੇ ਉਛਾਲਿਆ ਗਿਆ। ਜੇਕਰ ਸਿੱਕੇ ਤੇ ਚਿੱਤ ਆਉਂਦਾ ਹੈ, ਤਾਂ ਕੀ ਸੰਭਾਵਨਾ ਹੈ ਕਿ ਉਹ ਦੋਵੇਂ ਚਿੱਤ ਵਾਲੇ ਸਿੱਕੇ ਹਨ?
05:25View Solutionਇੱਕ ਬੀਮਾ ਕੰਪਨੀ 2000 ਸਕੂਟਰ ਚਾਲਕਾਂ, 4000 ਕਾਰ ਚਾਲਕਾਂ ਅਤੇ 6000 ਟਰੱਕ ਦਾ ਬੀਮਾ ਕਰਦੀ ਹੈ। ਦੁਰਘਟਨਾਵਾਂ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਕ੍ਰਮਵਾਰ: 0-01, 0-03 ਅਤੇ 0-15 ਹੈ। ਬੀਮਾ ਕਰਵਾਉਣ ਵਾਲੇ ਚਾਲਕਾਂ ਵਿੱਚੋਂ ਇੱਕ ਦੁਰਘਟਨਾ ਤੋਂ ਪੀੜਿਤ ਹੋ ਜਾਂਦਾ ਹੈ। ਉਸ ਵਿਅਕਤੀ ਦੇ ਸਕੂਟਰ ਚਾਲਕ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ?
06:43View Solutionਇੱਕ ਕਾਰਖਾਨੇ ਵਿੱਚ A ਅਤੇ B ਮਸ਼ੀਨਾਂ ਹਨ। ਪਹਿਲੇ ਵਿਵਰਨ ਤੋਂ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ ਕੁੱਲ ਪੈਦਾਵਾਰ ਦਾ 60% ਮਸ਼ੀਨ A ਅਤੇ 40% ਮਸ਼ੀਨ B ਰਾਹੀਂ ਪੈਦਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਮਸ਼ੀਨ A ਦਾ 2% ਅਤੇ ਮਸ਼ੀਨ B ਦਾ 1% ਪੈਦਾਵਾਰ ਖਰਾਬ ਹੈ। ਜੇਕਰ ਕੁੱਲ ਪੈਦਾਵਾਰ ਦਾ ਇੱਕ ਢੇਰ ਬਣਾ ਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਉਸ ਢੇਰ ਤੋਂ ਬੇਤਰਤੀਬੀ ਨਾਲ ਕੱਢੀ ਗਈ ਵਸਤੂ ਖਰਾਬ ਹੋਵੇ, ਤਾਂ ਇਸ ਵਸਤੂ ਦੇ ਮਸ਼ੀਨ A ਰਾਹੀਂ ਬਣੇ ਹੋਣ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ?
05:14View Solutionਦੋ ਟੋਲੀਆਂ ਇੱਕ ਨਿਗਮ ਦੇ ਨਿਦੇਸ਼ਕ ਮੰਡਲ ਵਿੱਚ ਪਦ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਮੁਕਾਬਲੇ ਵਿੱਚ ਹਨ। ਪਹਿਲੀ ਅਤੇ ਦੂਜੀ ਟੋਲੀ ਦੇ ਜਿੱਤਣ ਦੀ ਸੰਭਾਵਨਾਵਾਂ ਕ੍ਰਮਵਾਰ 0-6 ਅਤੇ 0-4 ਹਨ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਜੇਕਰ ਪਹਿਲੀ ਟੋਲੀ ਜਿੱਤਦੀ ਹੈ ਤਾਂ ਇੱਕ ਨਵੇਂ ਉਤਪਾਦ ਦੇ ਸ਼ੁਰੂ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ 0-7 ਹੈ ਅਤੇ ਜੇਕਰ ਦੂਜੀ ਟੋਲੀ ਜਿੱਤਦੀ ਹੈ ਤਾਂ ਇਸ ਗੱਲ ਦੀ ਸੰਗਤ ਸੰਭਾਵਨਾ 0-3 ਹੈ। ਇਸ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ਕਿ ਨਵਾਂ ਉਤਪਾਦ ਦੂਜੇ ਦਲ ਰਾਹੀਂ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਹੈ।
04:12View Solutionਮੰਨ ਲਉ ਕਿ ਕੋਈ ਕੁੜੀ ਇੱਕ ਪਾਸਾ ਸੁੱਟਦੀ ਹੈ। ਜੇਕਰ ਉਸਨੂੰ 5 ਜਾਂ 6 ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਹ ਇੱਕ ਸਿੱਕਾ ਤਿੰਨ ਵਾਰੀ ਉਛਾਲਦੀ ਹੈ ਅਤੇ ਚਿੱਤ ਆਉਣ ਦੀ ਗਿਣਤੀ ਨੋਟ ਕਰਦੀ ਹੈ। ਜੇਕਰ ਉਸਨੂੰ 1, 2, 3 ਜਾਂ 4 ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਹ ਇੱਕ ਸਿੱਕੇ ਆਉਣਾ ਇੱਕ ਵਾਰੀ ਉਛਾਲਦੀ ਹੈ ਅਤੇ ਇਹ ਨੋਟ ਕਰਦੀ ਹੈ ਕਿ ਉਸਤੇ ਚਿੱਤ ਜਾਂ ਪੱਟ ਆਉਂਦਾ ਹੈ। ਜੇਕਰ ਉਸਨੂੰ ਠੀਕ ਇੱਕ ਚਿੱਤ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਉਸਦੇ ਰਾਹੀਂ ਉਛਾਲੇ ਪਾਸੇ ਤੇ 1, 2, 3 ਜਾਂ 4 ਆਉਣ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ?
06:40View Solutionਇੱਕ ਨਿਰਮਾਤਾ ਦੇ ਕੋਲ A, B ਅਤੇ C ਮਸ਼ੀਨ ਆਪਰੇਟਰ ਹਨ। ਪਹਿਲਾ ਆਪਰੇਟਰ A 1% ਖਰਾਬ ਸਮੱਗਰੀ ਬਣਾਉਂਦਾ ਹੈ ਅਤੇ ਆਪਰੇਟਰ B ਅਤੇ C ਕ੍ਰਮਵਾਰ 5% ਅਤੇ 7% ਖਰਾਬ ਸਮੱਗਰੀ ਬਣਾੳਂਦੇ ਹਨ। ਕਾਰਜ ਤੇ A ਕੁੱਲ 50% ਸਮਾਂ ਲਗਾਉਂਦਾ ਹੈ, B ਕੁੱਲ ਸਮਾਂ ਦਾ 30% ਅਤੇ C ਕੁੱਲ ਸਮਾਂ ਦਾ 20% ਲਗਾਉਂਦਾ ਹੈ। ਜੇਕਰ ਇੱਕ ਖਰਾਬ ਸਮੱਗਰੀ ਬਣਦੀ ਹੈ ਤਾਂ ਉਸਨੂੰ A ਰਾਹੀਂ ਬਨਾਉਣ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ?
06:04View Solution52 ਪੱਤਿਆਂ ਦੀ ਤਾਸ਼ ਦੀ ਗੁੱਟੀ ਵਿੱਚੋਂ ਇੱਕ ਪਤਾ ਗਵਾਚ ਜਾਂਦਾ ਹੈ। ਬਾਕੀ ਪੱਤਿਆਂ ਵਿਚੋਂ ਦੋ ਪੱਤੇ ਕੱਢੇ ਜਾਂਦੇ ਹਨ ਜਿਹੜੇ ਇੱਟ ਦੇ ਹਨ। ਗਵਾਚੇ ਪੱਤੇ ਦੇ ਇੱਟ ਦੇ ਹੋਣ ਦੀ ਕੀ ਸੰਭਾਵਨਾ ਹੈ?
07:42View SolutionA ਰਾਹੀਂ ਸੱਚ ਬੋਲਣ ਦੀ ਸੰਭਾਵਨਾ `4/5` ਹੈ। ਇੱਕ ਸਿੱਕਾ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ A ਦੱਸਦਾ ਹੈ ਕਿ ਚਿੱਤ ਆਇਆ ਹੈ। ਅਸਲ ਵਿੱਚ ਚਿੱਤ ਆਉਣ ਦੀ ਸੰਭਾਵਨਾ ਹੈ:
04:20View Solutionਜੇਕਰ A ਅਤੇ B ਇਹੋ ਜਿਹੀਆਂ ਘਟਨਾਵਾਂ ਹਨ ਕਿ `AsubB` ਹੈ ਅਤੇ `P(B) ne 0` ਹੈ ਤਾਂ ਹੇਠਾਂ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਠੀਕ ਹੈ:
02:50View Solutionਦੱਸੋ ਕਿ ਹੇਠ ਲਿਖੀ ਸੰਭਾਵਨਾ ਵੰਡ ਵਿੱਚ ਕਿਹੜੇ ਇੱਕ ਬੇਤਰਤੀਬ ਚਲ ਲਈ ਸੰਭਵ ਨਹੀਂ ਹਨ। ਆਪਣਾ ਉੱਤਰ ਕਾਰਣ ਨਾਲ ਲਿਖੋ। `
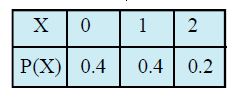 02:27View Solution
02:27View Solutionਦੱਸੋ ਕਿ ਹੇਠ ਲਿਖੀ ਸੰਭਾਵਨਾ ਵੰਡ ਵਿੱਚ ਕਿਹੜੇ ਇੱਕ ਬੇਤਰਤੀਬ ਚਲ ਲਈ ਸੰਭਵ ਨਹੀਂ ਹਨ। ਆਪਣਾ ਉੱਤਰ ਕਾਰਣ ਨਾਲ ਲਿਖੋ। `
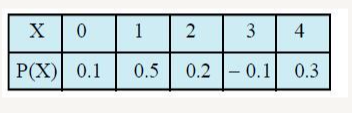 01:56View Solution
01:56View Solutionਦੱਸੋ ਕਿ ਹੇਠ ਲਿਖੀ ਸੰਭਾਵਨਾ ਵੰਡ ਵਿੱਚ ਕਿਹੜੇ ਇੱਕ ਬੇਤਰਤੀਬ ਚਲ ਲਈ ਸੰਭਵ ਨਹੀਂ ਹਨ। ਆਪਣਾ ਉੱਤਰ ਕਾਰਣ ਨਾਲ ਲਿਖੋ। `
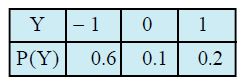 01:54View Solution
01:54View Solutionਦੱਸੋ ਕਿ ਹੇਠ ਲਿਖੀ ਸੰਭਾਵਨਾ ਵੰਡ ਵਿੱਚ ਕਿਹੜੇ ਇੱਕ ਬੇਤਰਤੀਬ ਚਲ ਲਈ ਸੰਭਵ ਨਹੀਂ ਹਨ। ਆਪਣਾ ਉੱਤਰ ਕਾਰਣ ਨਾਲ ਲਿਖੋ। `
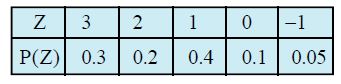 02:26View Solution
02:26View Solutionਇੱਕ ਕਲਸ਼ ਵਿੱਚ 5 ਲਾਲ ਅਤੇ 2 ਕਾਲੀਆਂ ਗੇਂਦਾਂ ਹਨ। ਦੋ ਗੇਂਦਾ ਬੇਤਰਤੀਬੀ ਨਾਲ ਕੱਢੀਆਂ ਗਈਆਂ। ਮੰਨ ਲਉ X ਕਾਲੀ ਗੇਂਦਾਂ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ। X ਦੇ ਸੰਭਾਵੀ ਮੁੱਲ ਕੀ ਹਨ? ਕੀ X ਬੇਤਰਤੀਬ ਚਲ ਹੈ?
02:41View Solutionਮੰਨ ਲਉ X ਚਿੱਤਾਂ ਦੀ ਗਿਣਤੀ ਅਤੇ ਪਟਾਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਅੰਤਰ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਜਦੋਂ ਇੱਕ ਸਿੱਕੇ ਨੂੰ 6 ਵਾਰੀ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ। X ਦੇ ਸੰਭਾਵੀ ਮੁੱਲ ਕੀ ਹਨ?
03:52View Solutionਇੱਕ ਸਿੱਕੇ ਦੀ ਦੋ ਉਛਾਲਾਂ ਵਿੱਚ ਚਿੱਤਾਂ ਦੀ ਗਿਣਤੀ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ।
02:15View Solutionਤਿੰਨ ਸਿੱਕਿਆਂ ਨੂੰ ਇੱਕੋ ਵਾਰੀ ਉਛਾਲਣ ਤੇ ਪਟਾਂ ਦੀ ਗਿਣਤੀ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ।
03:00View Solutionਇੱਕ ਸਿੱਕੇ ਦੀ ਚਾਰ ਉਛਾਲਾਂ ਵਿੱਚ ਚਿੱਤਾਂ ਦੀ ਗਿਣਤੀ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ।
05:14View Solutionਇੱਕ ਪਾਸਾ ਦੋ ਵਾਰੀ ਸੁੱਟਣ ਤੇ ਸਫਲਤਾ ਦੀ ਸੰਖਿਆ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ ਜਿੱਥੇ : 4 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ’ ਨੂੰ ਇੱਕ ਸਫਲਤਾ ਮੰਨਿਆ ਗਿਆ ਹੈ।
03:31View Solutionਇੱਕ ਪਾਸਾ ਦੋ ਵਾਰੀ ਸੁੱਟਣ ਤੇ ਸਫਲਤਾ ਦੀ ਸੰਖਿਆ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ ਜਿੱਥੇ : ਪਾਸੇ ਤੇ ਸੰਖਿਆ 6 ਆਉਣਾ’ ਨੂੰ ਸਫਲਤਾ ਮੰਨਿਆ ਗਿਆ ਹੈ।
03:47View Solution30 ਬਲਬਾਂ ਦੇ ਇੱਕ ਢੇਰ ਵਿੱਚੋਂ, ਵਿੱਚੋਂ 6 ਬਲਬ ਖਰਾਬ ਹਨ। 4 ਬਲਬ ਦਾ ਇੱਕ ਨਮੂਨਾ ਬੇਤਰਤੀਬੀ ਨਾਲ ਬਗੈਰ ਪੁਨਰ ਸਥਾਪਿਤ ਕੀਤਾ ਕੱਢਿਆ ਜਾਂਦਾ ਹੈ। ਖਰਾਬ ਬਲਬਾਂ ਦੀ ਸੰਖਿਆ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ।
07:09View Solutionਇੱਕ ਸਿੱਕਾ ਗੈਰ ਨਿਰਪੱਖ ਹੈ, ਜਿਸ ਵਿੱਚ ਚਿੱਤ ਆਉਣ ਦੀ ਸੰਭਾਵਨਾ ਪਟ ਆਉਣ ਤੋਂ ਤਿਗੁਣੀ ਹੈ। ਜੇਕਰ ਸਿੱਕਾ ਦੋ ਵਾਰੀ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਪਟਾਂ ਦੀ ਗਿਣਤੀ ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ।
05:07View Solutionਇੱਕ ਬੇਤਰਤੀਬ ਚਲ X ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਹੇਠ ਦਿੱਤਾ ਗਿਆ ਹੈ।

ਪਤਾ ਕਰੋ: `P (0ltXlt3)` ਪਤਾ ਕਰੋ: k02:53View Solutionਇੱਕ ਬੇਤਰਤੀਬ ਚਲ X ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਹੇਠ ਦਿੱਤਾ ਗਿਆ ਹੈ। `
 ਪਤਾ ਕਰੋ: `P(003:51View Solution
ਪਤਾ ਕਰੋ: `P(003:51View Solutionਇੱਕ ਬੇਤਰਤੀਬ ਚਲ X ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਹੇਠ ਦਿੱਤਾ ਗਿਆ ਹੈ।
 ਪਤਾ ਕਰੋ: `P(06)`04:19View Solution
ਪਤਾ ਕਰੋ: `P(06)`04:19View Solutionਇੱਕ ਬੇਤਰਤੀਬ ਚਲ X ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਹੇਠ ਦਿੱਤਾ ਗਿਆ ਹੈ। `
 03:46View Solution
03:46View Solutionਇੱਕ ਬੇਤਰਤੀਬ ਚਲ X ਸੰਭਾਵਨਾ ਫਲਨ P(x) ਹੇਠ ਪ੍ਰਕਾਰ ਹੈ, ਜਿੱਥੇ k ਕੋਈ ਸੰਖਿਆ ਹੈ: `P(x)={(k,,`ਜੇਕਰ,,`x=0),(2k,,`ਜੇਕਰ,,`x=1),(3k,,`ਜੇਕਰ,,`x=2),(0,,,,):}` k ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ।
02:05View Solutionਇੱਕ ਬੇਤਰਤੀਬ ਚਲ X ਸੰਭਾਵਨਾ ਫਲਨ P(x) ਹੇਠ ਪ੍ਰਕਾਰ ਹੈ, ਜਿੱਥੇ k ਕੋਈ ਸੰਖਿਆ ਹੈ: `P(x)={(k,,`ਜੇਕਰ,,`x=0),(2k,,`ਜੇਕਰ,,`x=1),(3k,,`ਜੇਕਰ,,`x=2),(0,,,,):}` `P(X<2), P(Xle2), P(Xge2)` ਪਤਾ ਕਰੋ।
04:26View Solutionਇੱਕ ਨਿਰਪੱਖ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾਰੀ ਉਛਾਲਣ ਤੇ ਪ੍ਰਾਪਤ ਚਿੱਤਾਂ ਦੀ ਸੰਖਿਆ ਦਾ ਮੱਧਮਾਨ ਪਤਾ ਕਰੋ।
04:25View Solutionਦੋ ਪਾਸਿਆਂ ਦੇ ਜੋੜੇ ਨੂੰ ਸੁੱਟਿਆ ਗਿਆ। ਜੇਕਰ X, ਛੇ ਦੀ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਤਾਂ X ਦਾ ਪੂਰਵ ਅਨੁਮਾਨ ਪਤਾ ਕਰੋ।
03:48View Solutionਪਹਿਲੀਆਂ ਛੇ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਵਿੱਚੋਂ ਦੋ ਸੰਖਿਆਵਾਂ ਬੇਤਰਤੀਬੀ (ਬਿਨਾ ਪੁਨਰ ਸਥਾਪਿਤ ਕੀਤੇ) ਨਾਲ ਚੁਣੀਆਂ ਗਈਆਂ। ਮੰਨ ਲਉ X ਦੋਵੇਂ ਸੰਖਿਆਵਾਂ ਵਿੱਚੋਂ ਵੱਡੀ ਸੰਖਿਆ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ। E(X) ਪਤਾ ਕਰੋ।
05:42View Solutionਮੰਨ ਲਉ ਦੋ ਪਾਸਿਆਂ ਨੂੰ ਸੁੱਟਣ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਨੂੰ X ਤੋਂ ਲਿਖਿਆ ਜਾਂਦਾ ਹੈ। X ਦਾ ਪ੍ਰਸਰਨ ਅਤੇ ਮਾਨਕ ਵਿਚਲਨ ਪਤਾ ਕਰੋ।
09:07View Solutionਇੱਕ ਜਮਾਤ ਵਿੱਚ 15 ਵਿਦਿਆਰਥੀ ਹਨ ਜਿਹਨਾਂ ਦੀ ਉਮਰ 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 ਅਤੇ 20 ਸਾਲ ਹੈ। ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਚੁਣਿਆ ਗਿਆ ਕਿ ਹਰੇਕ ਵਿਦਿਆਰਥੀ ਦੇ ਚੁਣੇ ਜਾਣ ਦੀ ਸੰਭਾਵਨਾ ਬਰਾਬਰ ਹੈ ਅਤੇ ਚੁਣੇ ਵਿਦਿਆਰਥੀ ਦੀ ਉਮਰ ਨੂੰ (X)ਨੂੰ ਲਿਖਿਆ ਗਿਆ। ਬੇਤਰਤੀਬ ਚਲ X ਦੀ ਸੰਭਾਵਨਾ ਵੰਡ ਪਤਾ ਕਰੋ। X ਦਾ ਮੱਧਮਾਨ, ਪ੍ਰਸਰਨ ਅਤੇ ਮਾਨਕ ਵਿਚਲਨ ਵੀ ਪਤਾ ਕਰੋ।
08:33View Solutionਇੱਕ ਬੈਠਕ ਵਿੱਚ 70% ਭਾਗੀਦਾਰਾਂ ਨੇ ਕਿਸੇ ਪ੍ਰਸਤਾਵ ਦਾ ਸਮਰਥਨ ਕੀਤਾ ਅਤੇ 30% ਭਾਗੀਦਾਰਾਂ ਨੇ ਵਿਰੋਧ ਕੀਤਾ। ਇੱਕ ਭਾਗੀਦਾਰ ਨੂੰ ਬੇਤਰਤੀਬ ਨਾਲ ਚੁਣਿਆ ਗਿਆ ਅਤੇ, ਜੇਕਰ ਉਸ ਭਾਗੀਦਾਰ ਨੇ ਪ੍ਰਸਤਾਵ ਦਾ ਵਿਰੋਧ ਕੀਤਾ ਹੋਵੇ ਤਾਂ `X = 0` ਲਿਆ ਗਿਆ, ਜਦੋਂ ਕਿ ਜੇਕਰ ਉਸਨੇ ਪ੍ਰਸਤਾਵ ਦਾ ਸਮਰਥਨ ਕੀਤਾ ਹੋਵੇ ਤਾਂ `X = 1` ਲਿਆ ਗਿਆ। `E(X)` ਅਤੇ `var (X)` ਪਤਾ ਕਰੋ।
03:51View Solutionਇਹੋ ਜਿਹੇ ਪਾਸੇ, ਜਿਸਦੇ ਤਿੰਨ ਫ਼ਲਨਾਂ ਤੇ 1 ,ਹੋਰ ਦੋ ’ਤੇ 2 ਅਤੇ ਇੱਕ ਪਾਸੇ ’ਤੇ 5 ਲਿਖਿਆ ਹੈ, ਨੂੰ ਸੁੱਟਣ ਤੇ ਪ੍ਰਾਪਤ ਸੰਖਿਆਵਾਂ ਦਾ ਮੱਧਮਾਨ ਹੈ :
03:35View Solution
Exercise questions and complete solutions for chapter ਸੰਭਾਵਨਾ of PSEB (PUNJABI MEDIUM) of Class 12
