Complete Solutions to PROBLEMS of chapter FLUIDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FLUIDS |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 68 |
| Academic Year | 2023-24 |
Giraffe bending to drink. In a giraffe with its head 1.8 m above its heart, and its heart 2.0 m above its feet, the (hydrostatic) gauge pressure in the blood at its heart is 250 torr. Assume that the giraffe stands upright and the blood density is `1.06 xx 10^(3) kg// m^(3)` . In torr (or mm Hg), find the (gauge) blood pressure (a) at the brain (the pressure is enough to perfuse the brain with blood, to keep the giraffe from fainting) and (b) at the feet (the pressure must be countered by tight-fitting skin acting like a pressure stocking). (c) If the giraffe were to lower its head to drink from a pond without splaying its legs and moving slowly, what would be the increase in the blood pressure in the brain? (Such action would probably be lethal.)
View SolutionThe fresh water behind a reservoir dam is `15 m` deep. A horizontal pipe `4.0 cm` in diameter passes through the dam `6.0 m` below the water surface as shown in the figure. A plug secures the pipe opening :
(a) Find the friction force between the plug and the pipe wall.
(b) The plug is removed. What volume of water flows out of the pipe in `3.0` hour ? Assume that reservoir is large.
 .
.
View SolutionIn Fig ., the fresh water stands at depth D = 30.0 m behind the vertical upstream face of a dam of width W = 250 m. Find (a) the net horizontal force on the dam from the gauge pressure of the water and (b) the net torque due to that force about a horizontal line through O parallel to the (long) width of the dam. This torque tends to rotate the dam around that line, which would cause the dam to fail. (c) Find the moment arm of the torque.

View SolutionThe volume of air space in the passenger compartment of an 1800 kg car is 5.00 `m^(3)` . The volume of the motor and front wheels is `0.710 m^(3)`, and the volume of the rear wheels, gas tank, and trunk is `0.800 m^(3)`, water cannot enter these two regions. The car rolls into a lake. (a) At first, no water enters the passenger compartment. How much of the car, in cubic meters, is below the water surface with the car floating (Fig. 14-45)? (b) As water slowly enters, the car sinks. How many cubic meters of water are in the car as it disappears below the water surface? (The car, with a heavy load in the trunk, remains horizontal.)

View SolutionThe maximum depth `d_(max)` that a diver can snorkel is set by the density of the water and the fact that human lungs can function against a maximum pressure difference between inside and outside the chest cavity) of 0.050 atm. What is the difference in `d_(max)` for fresh water and the water of the Dead Sea (the saltiest natural water in the world, with a density of `1.5 x 10^(3) kg//m^(3)`)?
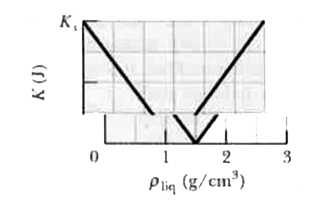
View SolutionA small solid ball is released from rest while fully sub merged in a liquid and then its kinetic energy is measured when it has moved 2.0 cm in the liquid. Figure 14.46 gives the results after many liquids are used: The kinetic energy K is plotted versus the liquid density `rho_(liq)` and `K_(s)` = 2.4 J sets the scale on the vertical axis. What are (a) the density and (b) the volume of the ball?
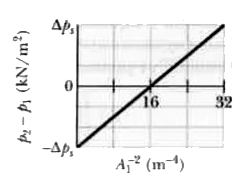
View SolutionFresh water flows horizontally from pipe section 1 of cross-sectional area A, into pipe section 2 of cross-sectional area `A_(2)` Figure gives a plot of the pressure difference `p_(2) - p_(1)` versus the inverse area squared `A_(1)^(-2)` that would be expected for a volume flow rate of a certain value if the water flow were laminar under all circumstances. The scale on the vertical axis is set by `Deltap_(s) = 600 kN//m^(2)`. For the conditions of the figure, what are the values of (a) `A_(2)` and (b) the volume flow rate?
View SolutionIn Fig. water flows steadily from the left pipe section (radius `r_(1)` = 2.00R), through the middle section (radius R), and into the right section (radius `r_(3)` = 3.00R). The speed of the water in the middle section is 0.620 m/s. What is the net work done on `0.700 m^(3)` of the water as it moves from the left section to the right section?
View SolutionA fluid is to be pushed through a narrow tube of radius 0.56 cm. What is the pressure increase in the fluid when the applied force is 120 N?
View SolutionA liquid of density 900 kg/m flows through a horizontal pipe that has a cross-sectional area of `1.90 xx 10^(-2) m^(2)` in region A and a cross-sectional area of `9.50 xx 10^(-2) m^(2)` in region B. The pressure difference between the two regions is `720 xx 10^(3)` Pa. What are (a) the volume flow rate and (b) the mass flow rate?
View SolutionThe plastic tube in Fig. has a cross-sectional area of 5.00 `cm^(2)`. The tube is filled with water until the short arm (of length d = 0.800 m) is full. Then the short arm is figure sealed and more water is gradually poured into the long arm. When the total height of water in the long arm reaches 2.80 m, the seal is on the verging of popping. What force is then on the seal?
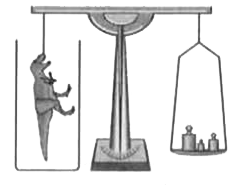
View SolutionWhen researchers find a reasonably complete fossil of a dinosaur, they can determine the mass and weight of the living dinosaur with a scale model sculpted from plastic and based on the dimensions of the fossil bones. The scale of the model is 1/20, that is, lengths are 1/20 actual length, areas are `(1//20)^(2)` actual areas, and volumes are `(1//20)^(3)` actual volumes. First, the model is suspended from One arm of a balance and weights are added to the other arm until equilibrium is reached. Then the model is fully submerged in water and enough weights are removed from the second arm to reestablish equilibrium (Fig. ). For a model of a particular T. rex fossil 791.10 g had to be removed to a reestablish equilibrium . what was the volume of (a) the model and (b) the actual T . rex ? (c) if the density of T.rex was approximately the density of water , what was its mass ?
View SolutionTwo streams merge to form a river. One stream has a width of 8.2 m, depth of 3.4 m, and current speed of 2.3 m/s. The other stream is 6.8 m wide and 3.2 m deep, and flows at 2.6 m/s. If the river has width 10.5 m and depth 4.5 m, what is its speed?
View SolutionA partially evacuated airtight container has a tight-fitting lid of surface area 50 `cm^(2)` and negligible mass. If the force required to remove the lid is 480 N and the atmospheric pressure is `1.0`x `10^(5)` Pa, what is the internal air pressure?
View SolutionA 3.00 kg object is released from rest while fully sub merged in a liquid. The liquid displaced by the submerged object has a mass of 5.00 kg. How far and in what direction does the object move in 0.200 s, assuming that it moves freely and that the drag force on it from the liquid is negligible?
View SolutionBlood pressure in Argentinosaurus. (a) If this long-necked, gigantic sauropod had a head height of 18 m and a heart height of 8.0 m, what (hydrostatic) gauge pressure in its blood was required at the heart such that the blood pressure at the brain was 80 torr (just enough to perfuse the brain with blood)? Assume the blood had a density of `1.06 xx 10 kg//m^(3)`. (b) What was the blood pressure (in torr or mm Hg) at the feet?
View SolutionA boat floating in fresh water displaces water weighing 50.1 KN. (a) What is the weight of the water this boat displaces when floating in salt water of density `1.10 xx 10^(3) kg//m^(3)` ? (b) What is the difference between the volume of fresh water displaced and the volume of salt water displaced?
View SolutionSnorkeling by humans and elephants. When a person snorkels, the lungs are connected directly to the atmosphere through the snorkel tube and thus are at atmospheric pressure. In atmospheres, what is the difference `Deltap` between this internal air pressure and the water pressure against the body if the length of the snorkel tube is (a) 20 cm (standard situation) and (b) 3.5 m (probably lethal situation)? In the latter, the pressure difference causes blood vessels on the walls of the lungs to rupture, releasing blood into the lungs. As depicted in Fig. 14-52, an elephant can safely snorkel through its trunk while swimming with its lungs 3.5 m below the water surface because the membrane around its lungs contains connective tissue that holds and protects the blood vessels, preventing rupturing.

View SolutionThree children, each of weight 356 N, make a log raft by lashing together logs of diameter 0.30 m and length 2.00 m. How many logs will be needed to keep them afloat in fresh water? Take the density of the logs to be 800 kg/`m^(3)`
View SolutionWhat gauge pressure must a machine produce in order to suck mud of density 1800 kg/`m^(3)` up a tube by a height of 2.0 m?
View SolutionA garden hose with an internal diameter of 1.9 cm is connected to a (stationary) lawn sprinkler that consists merely of a container with 20 holes, each 0.15 cm in diameter. If the water in the hose has a speed of 0.91 m/s, at what speed does it leave the sprinkler holes?
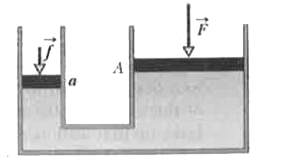
View SolutionA piston of cross-sectional area a is used in a hydraulic press to exert a small force of magnitude f on the enclosed liquid. A connecting pipe leads to o a larger piston of cross sectional area A (Fig. 14-53). (a) What force magnitude F will the larger piston sustain without moving? (b) If the piston diameters are 3.50 cm and 60.0 cm, what force magnitude on the large piston will balance a 20.0 N force on the small piston?
View SolutionHow much work is done by pressure in forcing `2.0 m^(3)` of water through a pipe having an internal diameter of 13 mm if the difference in pressure at the two ends of the pipe is 1.0 atm?
View SolutionCalculate the hydrostatic difference in blood pressure between the brain and the foot in a person of height 1.50 m. The density of blood is `1.06 xx 10^(3) kg//m^(3)`.
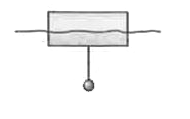
View SolutionFigure shows an iron ball suspended by thread of negligible mass from an upright cylinder that floats partially submerged in water. The cylinder has a height of 6.00 cm, a face area of `12.0 cm^(2)` on the top and bottom, and a density of `0.25 g//cm^(2)` , and 1.00 cm of its height is above the water surface. What is the radius of the iron ball?
View SolutionA flotation device is in the shape of a right cylinder, with a height of 0.650 m and a face area of `4.00 m^(2)` on top and bottom, and its density is 0.300 times that of fresh water. It is initially held fully submerged in fresh water, with its top face at the water surface. Then it is allowed to ascend gradually until it begins to float. How much work does the buoyant force do on the device during the ascent?
View SolutionSuppose that two tanks, 1 and 2, each with a large opening at the top, contain different liquids. A small hole is made in the side of each tank at the same depth h below the liquid surface, but the hole in tank 1 has half the cross-sectional area of the hole in tank 2. (a) What is the ratio `rho_(1) // rho_(2)` of the densities of the liquids if the mass flow rate is the same for the two holes? (b) What is the ratio `R_(v_(1))//R_(v_(2))` of the volume flow rates from the two tanks? (c) At one instant, the liquid in tank 1 is 16.0 cm above the hole. If the tanks are to have equal volume flow rates, what height above the hole must the liquid in tank 2 be just then?
View SolutionIn Fig. a spring of spring constant `3.75 xx 10^(4)` N/m Container is between a rigid beam Spring and the output piston of a hydraulic lever. An empty container with negligible mass sits on the input piston. The input piston has area `A_(i)` and the output piston has area `18.0A_(i)` Initially the spring is at its rest length. How many kilograms of sand must be (slowly) poured into the container to compress the spring by 5.00 cm?

View SolutionTwo identical cylindrical vessels with their bases at the same level each contain a liquid of density `1.30 xx 10^(3) kg//m^(3)`. The area of each base is `4.25 cm^(2)` , but in one vessel the liquid height is 0.854 m and in the other it is 1.560 m. Find the work done by the gravitational force in equalizing the levels when the two vessels are connected
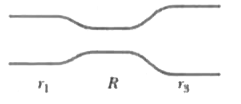
View SolutionFigure shows two sections of an old pipe system that runs through a hill, with distances `d_(A) = d_(B) = 40` m and D=110 m. On each side of the hill, the pipe radius is 2.00 cm. However, the radius of the pipe inside the hill is no longer known. To determine it, hydraulic engineers first establish that water flows through the left and right sections at 2.50 m/s. Then they release a dye in the water at point A and find that it takes 88.8 s to reach point B. What is the average radius of the pipe within the hill?

View SolutionA hollow spherical iron shell floats almost completely submerged in water. The outer diameter is 50.0 cm, and the density of iron is `7.87 g//cm^(3)` Find the inner diameter.
View SolutionAn office window has dimensions 3.4 m by 2.1 m. As a result of the passage of a storm, the outside air pressure drops to 0.93 atm, but inside the pressure is held at 1.0 atm. What net force pushes out on the window?
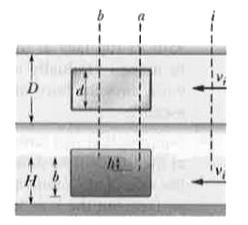
View SolutionCanal effect. Figure shows an anchored barge that extends across a canal by distance d = 30 m and into the water by distance b = 12 m. The canal has a width D = 55 m, a water depth H = 14 m, and a uniform water-flow speed `v_(i) = 1.2` m/s. Assume that the flow around the barge is uniform. As the water . passes the bow, the water level undergoes a dramatic dip known as the canal effect. If the dip has depth h = 0.80 m, what is the water speed alongside the boat through the vertical cross sections at (a) point a and (b) point b? The erosion due to the speed increase is a common concern to hydraulic engineers.
View SolutionWhat would be the height of the atmosphere if the air density (a) were uniform and (b) decreased linearly to zero with height? Assume that at sea level the air pressure is 1.0 atm and the air density is 1.3 kg/`m^(3)`
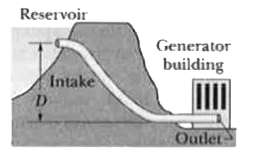
View SolutionThe intake in Figure, Reservoir has cross-sectional area of `0.740 m^(2)` and water flows in at 0.400 m/s. At the outlet, the cross-sectional area is smaller than at the intake and the water flows out at 9.50 m/s. The pressure difference between intake and outlet is 3.00 MPa. What is vertical distance D?
View SolutionA cylindrical tank with a large diameter is filled with water to a depth D =0.30 m. A hole of cross-sectional area A = 6.2 `cm^(2)` in the bottom of the tank allows water to drain out. (a) What is the drainage rate in cubic meters per second? (b) At what distance below the bottom of the tank is the cross-sectional area of the stream equal to one half the area of the hole?
View SolutionYou inflate the front tires on your car to 32 psi. Later, you measure your blood pressure, obtaining a reading of 135/70, the readings being in mm Hg. In metric countries (which is to say, most of the world), these pressures are customarily reported in kilopascals (kPa). In kilopascals, what are (a) your tire pressure and (b) your blood pressure?
View SolutionIf you can produce a minimum gauge pressure of `-2.5 xx 10^(-3)` atm in your lungs, to what maximum height can you suck tea (density 1000 kg/`m^(3)` ) up a straw?
View SolutionThe water flowing through a 1.9 cm (inside diameter) pipe flows out through three 1.5 cm pipes. (a) If the flow rates in the three smaller pipes are 26, 21, and 16 L/min, what is the flow rate in the 1.9 cm pipe? (b) What is the ratio of the speed in the 1.9 cm pipe to that in the pipe carrying 26 L/min?
View SolutionAn inflatable device with a density of 1.20 g/`cm^(3)` is fully submerged in fresh water and then inflated enough for the device's density to match that of the water. What then is the ratio of the expanded volume to the full volume of the device?
View SolutionFigure shows a stream of water flowing through a hole at depth h = 12 cm in a tank holding water to height H = 40 cm. (a) At what distance x does the stream strike the floor? (b) At what depth should a second hole be made to give the same value of x? (c) At what depth should a hole be made to maximize x?

View SolutionA large aquarium of height 5.00 m is filled with fresh water to a depth of 2.00 m. One wall of the aquarium consists of thick plastic 9.00 m wide. By how much does the total force on that wall increase if the aquarium is next filled to a depth of 4.00 m?
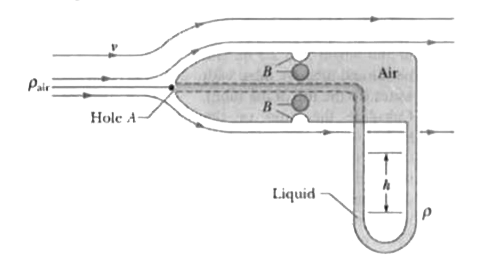
View SolutionA pitot tube Fig. is used to determine the air speed of an airplane. It consists of an outer tube with a number of small holes B (four are shown that allow air into the tube, that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that `v_(A)` = 0. At B, however, the speed of the air presumably equals the airspeed v of the plane. (a) Use Bernoulli's equation to show that
`v = sqrt((2rho gh)/(rho_(air)))`
where `rho` is the density of the liquid in the U-tube and his the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference h is 20.0 cm. What is the plane's speed relative to the air? The density of the air is `1.03 kg//m^(3)` and that of alcohol is 810 kg/`m^(3)`
View SolutionA pitot tube (see Problem 46) on a high-altitude aircraft measures a differential pressure of 150 Pa. What is the air craft's airspeed if the density of the air is `0.031 kg//m^(3)` ?
View SolutionModels of torpedoes are sometimes tested in a horizontal pipe of flowing water, much as a wind tunnel is used to test model airplanes. Consider a circular pipe of internal diameter 25.0 cm and a torpedo model aligned along the long axis of the pipe. The model has a 6,00 cm diameter and is to be tested with water flowing past it at 2.00 m/s. (a) With what speed must the water flow in the part of the pipe that is unconstricted by the model? (b) What will the pressure difference be between the constricted and unconstricted parts of the pipe?
View SolutionIn one observation, the column in a mercury barometer (as is shown in Fig. ) has a measured height h of 740.35 mm. The temperature is `-5.0^(@)` C, at which temperature the density of mercury `rho` is `1.3608 xx 10^(4) kg//m^(3)` . The free-fall acceleration g at the site of the barometer is 9.7828 m/`s^(2)`. What is the atmospheric pressure at thal site in pascals and in torr (which is the common unit for barometer readings)?
View SolutionWhat fraction of the volume of an iceberg (density 917kg/`m^(3)` ) would be visible if the iceberg floats (A) in the ocean (salt water density 1024kg/`m^(3)`) and (B) in a river (fresh water density 1000 kg/`m^(3)` )?(when salt water freezes to form ice, the salt is excluded. So an iceberg could provide fresh water to a community)
View SolutionWater is pumped steadily out of a flooded basement at 4.5 m/s through a hose of radius 1.0 cm, passing through a window 3.5 m above the waterline. What is the pump's power?
View SolutionAt a depth of 10.9 km, the Challenger Deep in the Marianas Trench of the Pacific Ocean is the deepest site in any ocean. Yet, in 1960, Donald Walsh and Jacques Piccard reached the Challenger Deep in the bathyscaph Trieste. Assuming that seawater has a uniform density of 1024 kg/`m^(3)`, approximate the hydrostatic pressure (in atmospheres) that the Trieste had to withstand. (Even a slight defect in the Trieste structure would have been disastrous.)
View SolutionA water pipe having a 2.5 cm inside diameter carries water into the basement of a house at a speed of 0.90 m/s and a pressure of 190 kPa. If the pipe tapers to 1.2 cm and rises to the second floor 7.6 m above the input point, what are the (a) speed and (b) water pressure at the second floor ?
View SolutionA hollow sphere of inner radius 8.0 cm and outer radius 9.0 cm floats half-submerged in a liquid of density 820 kg/`m^(3)`. (a) What is the mass of the sphere? (b) Calculate the density of the material of which the sphere is made.
View SolutionIn Fig. water flows through a horizontal pipe and then out into the atmosphere at a speed `v_(1)` = 23.0 m/s. The diameters of the left and right sections of the pipe are 5.00 cm and 3.00 сm. (a) What volume of water flows into the atmosphere during a 20.0 min period? In the left section of the pipe, what are (b) the speed `v_(2)` and (c) the gauge pressure?

View SolutionThree liquids that will not mix are poured into a cylindrical container. The volumes and densities of the liquids are 1.50 L, 2.6 g/`cm^(3)`: 0.75 L, 1.0 g/`cm^(3)` , and 0.60 L, 0.80 g/`cm^(3)`. What is the force on the bottom of the container due to these liquids? One liter = 1 L = 1000 `cm^(3)` (Ignore the contribution due to the atmosphere.)
View SolutionConsider the venturi tube of Sample Problem 14.21 and Fig.without the manometer. Let A equal 5a. Suppose the pressure `p_(1)` at A is 3.0 atm. Compute the values of (a) the speed V at A and (b) the speed vat a that make the pressure `p_(2)` , at a equal to zero. (c) Compute the corresponding volume flow rate if the diameter at A is 5.0 cm. The phenomenon that occurs at a when p, falls to nearly zero is known as cavitation. The water vaporizes into small bubbles.
View SolutionIn 1654 Otto von Guericke, inventor of the air pump, gave a demonstration before the noble-men of the Holy Roman Empire in which two teams of eight horses could not pull apart two evacuated brass hemispheres. (a) Assuming the hemispheres have (strong) thin walls, so that R in Fig. 14-63 may be considered both the inside and outside radius, show that the force `vecF` required to pull apart the hemispheres has magnitude `F = pi R^(2) Deltap`, where `Deltap` is the difference between the pressures outside and inside the sphere,
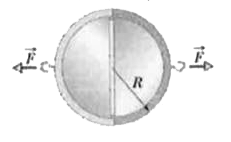
(b) Taking R as 40 cm, the inside pressure as 0.10 atm, and the outside pressure as 1.00 atm, find the force magnitude the teams of horses would have had to exert to pull apart the hemispheres. (c) Explain why one team of horses could have proved the point just as well if the hemispheres were attached to a sturdy wall.
View SolutionA wood block (mass 3.67 kg, density 600 kg/m) is fitted with lead (density `1.14 xx 10^(4) kg//m^(3)`) so that it floats in water with 0.700 of its volume submerged. Find the lead mass if the lead is fitted to the block's (a) top and (b) bottom
View SolutionA block of wood floats in fresh water with two-thirds of its volume V submerged and in oil with 0.92V submerged. Find the density of (a) the wood and (b) the oil.
View SolutionWater is moving with a speed of 5.0 m/s through a pipe with a cross-sectional area of `4.0 cm^(2)`. The water gradually descends 12 m as the pipe cross-sectional area increases to `8.0 cm^(2)` (a) What is the speed at the lower level? (b) If the pressure at the upper level is `1.5 xx 10^(5)` Pa, what is the pressure at the lower level?
View SolutionCrew members attempt to escape from a damaged submarine 100 m below the surface. What force must be applied to a pop-out hatch, which is 1.2 m by 0.60 m, to push it out at that depth? Assume that the density of the ocean water is 1024 kg/`m^(3)` and the internal air pressure is at 1.00 atm.
View SolutionA very simplified schematic of the rain drainage system for a home is shown in Fig. Rain falling on the slanted roof runs off into gutters around the roof edge, it then drains through downspouts (only one is shown) into a main drainage pipe M below the basement, which carries the water to an even larger pipe below the street. In Fig. a floor drain in the basement is also connected to drainage pipe M. Suppose the following apply:
(1) the downspouts have height `h_(1)` = 11 m,
(2) the floor drain has height `h_(2)` = 1.2 m,
(3) pipe M has radius 2.0 cm,
(4) the house has side width w = 40 m and front length L = 70 m,
(5) all the water striking the roof goes through pipe M,
(6) the initial speed of the water in a downspout is negligible, and
(7) the wind speed is negligible (the rain falls vertically).
At what rainfall rate, in centimeters per hour, will water from pipe M reach the height of the floor drain and threaten to flood the basement?

View SolutionAn iron anchor of density 7870 kg/`m^(3)` appears 200 N lighter in water than in air. (a) What is the volume of the anchor? (b) How much does it weigh in air?
View SolutionAn iron casting containing a number of cavities weighs 6000 N in air and 4200 N in water. What is the total cavity volume in the casting? The density of solid iron is 7.87 g/`cm^(3)`
View SolutionSuppose that you release a small ball from rest at a depth of 0.400 m below the surface in a pool of water. If the density of the ball is 0.450 that of water and if the drag force on the ball from the water is negligible, how high above the water surface will the ball shoot as it emerges from the water? (Neglect any transfer of energy to the splashing and waves produced by the emerging ball.)
View SolutionIn Fig. an open tube of length L = 2.3 m and crosssectional area A = 9.2 `cm^(2)` is fixed to the top of a cylindrical barrel of diameter D = 1.2 m and height H = 2.3 m. The barrel and tube are filled with water to the top of the tube). Calculate the ratio of the hydrostatic force on the bottom of the barrel to the gravitational force on the water contained in the barrel. Why is that ratio not equal to 1.0? (You need not consider the atmospheric pressure.)

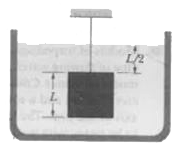
View SolutionIn Fig. a cube of edge length L=0.500 m and mass 450 kg is suspended by a rope in an open tank of liquid of density 1030 kg/`m^(3)`. Find (a) the magnitude of the total downward force on the top of the cube from the liquid and the atmosphere, assuming atmospheric pressure is 1.00 atm, (b) the magnitude of the total upward force on the bottom of the cube, and (c) the tension in the rope. (d) Calculate the magnitude of the buoyant force on the cube using Archimedes' principle. What relation exists among all these quantities?
View SolutionThe bends during flight. Anyone who scuba dives is advised not to fly within the next 24 h because the air mixture for diving can introduce nitrogen to the bloodstream. Without allowing the nitrogen to come out of solution slowly, any sudden air-pressure reduction (such as during airplane ascent) can result in the nitrogen forming bubbles in the blood, creating the bends, which can be painful and even fatal. Military special operation forces are especially at risk. What is the change in pressure on such a special-op soldier who must scuba dive at a depth of 25 m in seawater one day and parachute at an altitude of 8.1 km the next day? Assume that the average air density within the altitude range is 0.87 kg/`m^(3)`.
View SolutionIf Fig. 14-67a , a rectangular block is gradually pushed facedown into a liquid . The block has height d, on the bottom and top the face area is A = `8.00 cm^(2)` . Figure gives the apparent weight `W_(app)` of the block as a function of the depth h of its lower face . The scale on the vertical axis is set by `W_a = 0.20` N . What is the density of the liquid ?

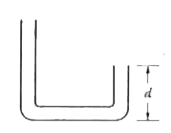
View SolutionThe L-shaped fish tank shown in Fig. is filled with water and is open at the top . Here , d = 70 m .
(a) What is the (total) force exerted by the water on face A ?
(b) What is the (total) force exerted by the water on face B ?
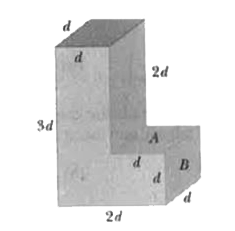
View Solution
PROBLEMS questions and complete solutions for chapter FLUIDS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12
All Exercises from RESNICK AND HALLIDAY Class 12 PHYSICS FLUIDS
- CHECKPOINT
- PRACTICE QUESTIONS (More than One Correct Choice Type )
- PRACTICE QUESTIONS (Integer Type )
- PRACTICE QUESTIONS (Linked Comprehension )
- PRACTICE QUESTIONS (Matrix - Match )
- PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
- PROBLEMS
- SAMPLE PROBLEM 14.01
- SAMPLE PROBLEM 14.02
- SAMPLE PROBLEM 14.03
- SAMPLE PROBLEM 14.04
- SAMPLE PROBLEM 14.05
- SAMPLE PROBLEM 14.06
- SAMPLE PROBLEM 14.07
- SAMPLE PROBLEM 14.08
- SAMPLE PROBLEM 14.09
- SAMPLE PROBLEM 14.10
- SAMPLE PROBLEM 14.11
- SAMPLE PROBLEM 14.12
- SAMPLE PROBLEM 14.13
- SAMPLE PROBLEM 14.14
- SAMPLE PROBLEM 14.15
- SAMPLE PROBLEM 14.16
- SAMPLE PROBLEM 14.17
- SAMPLE PROBLEM 14.18
- SAMPLE PROBLEM 14.19
- SAMPLE PROBLEM 14.20
- SAMPLE PROBLEM 14.21
- SAMPLE PROBLEM 14.22
- SAMPLE PROBLEM 14.23
- SAMPLE PROBLEM 14.24
- SAMPLE PROBLEM 14.25
- SAMPLE PROBLEM 14.26
- SAMPLE PROBLEM 14.27
- SAMPLE PROBLEM 14.28
- SAMPLE PROBLEM 14.29