Complete Solutions to PROBLEMS of chapter HEAT-MEASUREMENT AND TRANSFER of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | HEAT-MEASUREMENT AND TRANSFER |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
An 8.00 g ice cube at its melting point is added to `130 cm^(3)` of tea (water ) initially at `90.0^(@)C` in a well-insulated container. When equilibriu is reached, what has been the decrease in the tea's temperature ?
View SolutionA certain substance has a mass per mole of 50.0 `g//` mol. When 325 J is added as heat to a 30.0 g sample, the sample's temperature rises from `25.0^(@)` to `45.0^(@)` C. What are the (a) specific heat and (b) molar specific heat of this substance ? (c ) How many moles are in the sample ?
View SolutionOne way to keep the contents of a garage from becoming too cold on a night when a severe subfreezing temperature is forecast is to put a tub of water subfreezing temperature is forecast is to put a tub of water in the garage. If the mass of the water is 135 kg and its initial temperature is `20^(@)C`, (a) how much energy must the water transfer to its surrounding in order to freeze competely and (b) what is the lowest possible temperature of the water and its surrounding until that happens?
View SolutionNonmetric version `:` (a) How long does a `2.0 xx 10^(5)` Btu`//` h water heater take to raise the temperature of 65 gal of water from `70^(@)`F to `100^(@)F` ? Metric version `:` (b) How long does a 59 kW water heater take to raise the temperature of 246L of water from `21^(@)` to `38^(@)`C ?
View SolutionA small electric immersion heater is used to heat 170g of water for a cup of instant coffee. The heater is labeled "180 watts" ( it converts electrical enery to thermal energy at this rate ). Calculate the time required to bring all this water from `23.0^(@)C` to `100^(@)C`, ignoring any heat losses.
View SolutionA 3.0 cm slabe has formed on an outdoor tank of water . The air is at `-14^(@)C`. Find the rate of ice formation (centimeters per hour). The ice has thermal conductivity 0.0040 cal`//s.cm.""^(@)C` and density `0.92g //cm^(3)`.Assume there is no energy transfer through the walls or bottom.

View SolutionThe specific heat of a substance varies with temperature according to the function c = 0.20` +` 0.14 T` + 0.023T^(@)`, with T in `""^(@)C` and c in `Cal//g.K`, Find the energy required to raise the temperature of 1.0g of this substance from `5.0 ""^(@)C` to `15""^(@)C`.
View SolutionLeidenfrost effect. A water drop will last about 1 s on a hot skillet with a temperature between `100^(@)C` and about `200^(@0`. However, if the skillet is much hotter, the drop can last several minutes, an effect named after an early investigator. The longer lifetime is due to the support of a thin layer of air and water vapor that separates the drop from the metal ( by distance L in Figure ) . Let L = 0.0800 mm, and assume that the drop is flate with height h = 1.50 mm and bottom face area `A = 5.00 xx 10^(-6) m^(2)`. Also assume that the skilled has a constant temperature `T_(s) = 300^(@)C` and the drop has a temperature of `100^(@)C`.Water has density `rho=1000 kg//m^(3)`, and the supporting layer has thermal conductivity `k = 0.026 W//m. K`. (a) At what rate is energy conducted from the skillet to the drop through the drop's bottom surface? (b) If conduction is the primary way energy moves from the skilled to the drop, how long will the drop last ?

View SolutionEthyl alcohol has a boiling point of `78.0^(@)C`, a freezing point of `-114^(@)C`, a heat of vaporization of 879 kJ `//kg`, a heat of fusion of 109kJ `//`kg , and a specific heat of 2.43 kJ `//kg.K`. How much energy must be removed from 0.720kg of ethyl alcohol that is initially a gas at `78.0^(@)C` so that it becomes a solid at `- 114^(@)C` ?
View SolutionFigure shows the cross section of a wall made of three layers. The layer thicknesses are `L_(1), L_(2) = 0.750L_(1), ` and `L_(3) = 0.350L_(1)`. The thermal conductivities are `k_(1), k_(2) = 0.900k_(1)`, and `k_(3) = 0.800k_(1)`. The temperature at the left side and right side of the wall are `T_(H) = 30.0^(@)C` and `T_(C)= - 15.0^(@)C`, respectively. Thermal conduction is steady . (a) What is the temperature difference `Delta T_(2)` across layer 2 ( between the left and right sides of the layer ) ? If `k_(2)` were, instead, equal to 1.1`k_(1)`, (b) would the reate at which energy is conducted through the wall be greater than, less than, or the same as proviously, and (c ) what would be the value of `Delta T_(2)` ?
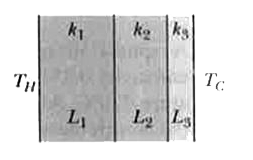
View SolutionConsider the slabe shown in Figure. Suppose that L = 15.0 cm , A `= 105 cm^(2)`, and the material is copper. If `T_(H) = 125^(@)C, T_(C ) = 10.0^(@)C`, and a steady state is reached, find the conduction rate through the slabe.
View SolutionWhat mass of steam at `100^(@)C` must be mixed with 250g of ice at its melting point, in a thermally insulated container, to produce liquid water at `50^(@)C` ?
View SolutionEvaporative cooling of beverages. A cold beverage can be kept cold even on a warm day if it is slipped into a porous ceramic container that has been soaked in water. Assume that energy lost to evaporation matched the net energy gained via the radiation exchange through the top and side surfaces. The container and beverage have temperature `T = 10^(@)C`, the environment has temperature `T_("env") = 32^(@)C`, and the container is a cylinder with radius `r = 2.2 cm` and height 10cm. Approximate the emissivity as `epsilon =1`, and neglect other energy exchanges .At what rate dm`//` dt is the container losing water mass ?
View SolutionA solid cylinder of radius `r_(1) = 2.5cm` , length `h_(1) = 5.5 ` cm, emissivity 0.85, and temperature `30^(@)C` is suspended in an environment of temperature `50^(@)C`. (a) What is the cylinder's net thermal radiation transfer rate `P_(1)` ? (b) If the cylinder is stretched until its radius is `r_(2) = 0.50 cm` , its net thermal radiation transfer rate becomes `P_(2)`. What is the ratio `P_(2)//P_(1)` ?
View SolutionFigure shows ( in cross section ) a wall consisting of four layers, with thermal conductivities `k_(1) = 0.060W//m.K, k_(3)= 0.040W//m.K`, and `k_(4) = 0.12W//m.K(k_(2)` is not known). The layer thickness are `L_(1) = 1.2 cm, L_(3) = 5.6 cm`, and `L_(4) = 4.0 cm` `( L_(2)` is not known ) . The known temperatures are `T_(1) = 30^(@)C, T_(12) = 25^(@)C`, and `T_(4) = - 10^(@) C` . Energy transfer through the wall is steady. What is interface temperature `T_(34)` ?

View SolutionA sphere of radius 0.350m, temperature `27.0^(@)C` , and emissivity 0.850 is located in an environment of temperature `77.0^(@)C`. At what rate does the sphere (a) emit and (b) absorb thermal radiation ? (c ) What is the sphere's net change in energy in 3.50 min ?
View SolutionIf you were to walk brieftly in space without a spacesuit while far from the Sun ( as an astronaut does in the movie 2001, A Space Odyssey ), you would feel the cold of space- while you radiated energy, you would absorb almost non from your environment . (a) At what rate would you lose energy ? (b) How much energy would you lose in 44s ? Assume that your emissivity is 0.90, and estimate other data needed in the calculations.
View SolutionIce has formed on a shallow pond, and a steady state has been reached, with the air above the ice at `- 5.0^(@)C` and the bottom of the pond at `4.0^(@)C`. If the total depth of ice `+` water is 2.0m, how thick is the ice ? (Assume that the thermal conductivity of ice and water are 0.40 and 0.12 `cal//m.""^(@)C.s`, respectively. )
View SolutionPenguin huddling.To withstand the harsh weather of the Antartic, emperor penguins huddle in groups ( Figure ). Assume that a penguins is a circular cylinder with a top surface area a = `0.26 m^(2)` ,and height h = 90 cm. Let `P_(r )` be the rate at which an individual penduin radiates energy to the environment (through the top and the sides ), thus `NP_(r )` is the rate at which N identical, well separated penguins radiate. if the penduins radiate. If the penguis huddle closely to form a huddled cylinder with top surface area Na and height h, the cylinder radiates at the rate `P_(h)`. If N = 1000, (a) what is the value of the fraction `P_(h) //NP_(r )` and (b) by what percentage does huddling reduces the total radiation loss ?

View SolutionThe giant hornet Vespa mandarinia japonica preys on Japanes bees.However, if one of the hornets attempts to invade a beehive, several hundred of the bees quickly form a compact ball around the hornet to stop it. They do not sting, bits, crush , or suffocate it. Rather they overheat it by quickly raising their body temperatures from the normal `35^(@)C` to `47^(@)` or `48^(@)C`, which is lethal to the hornet but not to bees (Figure ). Assume the following `:` 500 bees from a ball of radius R = 1.8 cm for a time t = 18 min, the primary loss of energy by the ball is by thermal radiation, the ball's surface has emissivity `epsilon = 0.80`, and the ball has a uniform temperature . On average, how much additional energy must each bee produce during the 18 min to maintain `47^(@)C` ?

View SolutionCalculate the minimum amount of energy, in joules, required to completely melt 85.0g of silver initially at `15.0^(@)C`.
View SolutionWhat mass of butter, which has a usable energy content of `6.0 KCal //g ( = 6000 cal //g )` , would be equivalent to the change in gravitational potential energy of a 78.0 kg man who ascends from sea level to the top of Mt. Everset, at elevation 8.84 km? Assume that the average g for the ascent is `9.80 m//s^(2)`.
View Solution(a) Two 40g ice cubes are droped into 200g of water in a thermally insulated container. If the water is initially at `25^(@)C`, and the ice comes directly from a freezer at `- 15^(@)C`, what is the final temperature at thermal equilibrium? (b) What is the final temperature if only one ice cube is used ?
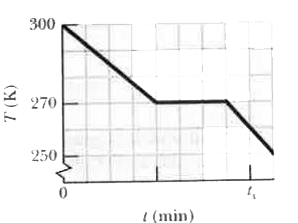
View SolutionA 0.600kg sample is placed in a cooling apparatus that removes energy as heat at a constant rate. Figure gives the temperature T of the sample versus time t, the horizontal scale is set by `t_(s) = 80.0` min. The sample freezes during the energy removal. The specific heat of the sample in its initial liquid phase is 3000`J//kg.K`. What are (a) the sample's heat of fusion and (b) its specific heat in the frozen phase ?
View SolutionA cylindrical copper rod of length 0.60m and cross-sectional area 6.0 `cm^(2)` is insulated along its side. The ends are held at a temperature difference of `100^(@)C` by having one end in a water -ice mixture and the other in a mixture of boiling water and steam. At what reate (a) is energy conducted by the rod and (b) does the ice melt ?
View SolutionIn a solar water heater, energy from the Sun is gathered by water that circulates through tubes in a rooftop collector. The solar radiation enters the collector through a transparent cover and warms the water in the tubes, this water is pumped into a holding tank. Assume that the efficiency of the overally system is `25%` ( that is, 80% of the incident solar energy is lost from the system ). What collector area is necessary to raise the temperature of 200L of water in the tank from `20^(@)C` to `40^(@)` in 1.0 h when the intensity of incident sunlight is 750 W`// m^(2)` ?
View SolutionA person makes a quantity of iced tea by mixing 250g of hot tea (essentially wwater ) with an equal mass of ice at its melting point.Assume the mixture has negligible energy exchange with its environment. If the tea's initial temperature is `T_(i) = 90^(@)C`, when thermal equilibrium is reached what are (a) the mixture's temperature `T_(f)` and (b) the remaining mass `m_(f )` of ice ? If `T_(i) = 70^(@)C`, when thermal equilibrium is reached what are (c ) `T_(f)` and (d) `m_(f )` ?
View SolutionA 150 g copper bowl contains 260 g of water, both at `20.0^(@)C` A very hot 300 g copper cylinder is dropped into the water, causing the water to boil, with 5.00 g being converted to steam. The final temperature of the system is `100^(@)C`. Neglect energy transfers with the environment. (a) How much energy ( in calories ) is transferred to the water as heat ? (b) How much to the bowl ? ( c ) What is the original temperature of the cylinder ?
View SolutionThe temperature of a body falls from `40^(@)C` to `36^(@)C` in `5` minutes when placed in a surrounding of constant temperature `16^(@)C`. Find the time taken for the temperature of the body to become `32^(@)C`.
View SolutionThe earth receives solar radiation at a rate of `8.2Jcm^(-2)min^(-1)` . Assuming that the sun radiates like a blackbody, Calculate the surface temperature of the sun. The angle subtended by the sun on the earth is `0.55^(@)C` and the stefan constant `sigma=5.67xx10^(-s)Wm^(-2)K^(-4)` .
View SolutionA hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being `k` times the temperature difference from the surrounding. Starting from `t=0` , find the time in which the body will loss half the maximum heat it can lose.
View Solution(a) Calculate the rate at which body heat is conducted through the clothing of a skier in a steady-state process, given the following data`:` the body surface area is `1.8m^(2)`, and the clothing is 1.0 cm thick , the skin surface temperature is `33^(@)C` and the outer surface of the clothing is at `1.0^(@)C`, the thermal conductivity of the clothing is `0.040 W//m . K.` (b) If , after a fall, the skier's clothes became soaked with water of thermal conductivity `0.60 W//m.K`, by how much is the rate of conduction multiplied ?
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure `(theta_(2)gttheta_(1))` . Thermal conductivity of the material of the rod is `K`.

View SolutionA calorimeter containes `50g` of water at `50^(@)C` . The temperature falls to `45^(@)C` in `10` minutes. When the calorimeter contains `100g` of water at `50^(@)C` it takes `18` minutes for the temperature to become `45^(@)C` . Find the water equivalent of the calorimeter.
View SolutionA metal ball of mass `1kg` is heated by means of a `20W` heater in a room at `20^(@)C` . The temperature of the ball becomes steady at `50^(@)C` . (a) Find the rate of loss of heat to the surrounding when the ball is at `50^(@)C` . (b) Assuming Newton's law of cooling, calculate the rate of loss of heat to the surrounding when the ball is at `30^(@)C` . (c) Assume that the temperature of the ball rises uniformly from `20^(@)C` to `30^(@)C` in `5` minutes. Find the total loss of heat to the surrounding during this period. (d) Calculate the specific heat capacity of the metal.
View Solution
PROBLEMS questions and complete solutions for chapter HEAT-MEASUREMENT AND TRANSFER of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12
All Exercises from RESNICK AND HALLIDAY Class 12 PHYSICS HEAT-MEASUREMENT AND TRANSFER
- CHECKPOINT 1
- CHECKPOINT 2
- PRACTICE QUESTIONS
- PRACTICE QUESTIONS( INTEGER TYPE)
- PRACTICE QUESTIONS( LINKED COMPREHENSION)
- PRACTICE QUESTIONS(MORE THAN ONE CORRECT CHOICE TYPE )
- PROBLEMS
- SOLVED PROBLEM 19.01
- SOLVED PROBLEM 19.02
- SOLVED PROBLEM 19.03
- SOLVED PROBLEM 19.04
- SOLVED PROBLEM 19.05
- SOLVED PROBLEM 19.06
- SOLVED PROBLEM 19.07
- SOLVED PROBLEM 19.08