Complete Solutions to PRACTICE QUESTIONS (Linked Comprehension) of chapter THE NUCLEUS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THE NUCLEUS |
| RESNICK AND HALLIDAY | PRACTICE QUESTIONS (Linked Comprehension) |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
Gold nucleus `(""_(79)^(198)Au)` can decay into mercuyr nucleus `(""_(80)^(198)Hg^(8))` by two decay schemes shown in figure below (i) it can emit a `beta` -particle `(beta_(1))` and come to ground state by either emiting one `gamma`- ray (` gamma_(1)`) or emitting two `gamma`- rays (`gamma_(3)` and `gamma_(4)`) (ii) It can emit one `beta`- particle `(beta_(2))` and come to ground state by emitting `gamma_(2)` ray. Atomic masses: `""^(198)Au=197.9652` amu and `""^(198)Hg=197.9662` amu. Given that 1 amu= `930MeV//c^(2)`. The energy levels of the nucleus are shown in figure below
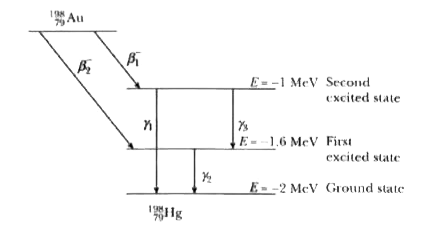
Whatis the maximum kinetic energy of emitted `beta_(2)` particle?
View SolutionGold nucleus `(""_(79)^(198)Au)` can decay into mercuyr nucleus `(""_(80)^(198)Hg^(8))` by two decay schemes shown in figure below (i) it can emit a `beta` -particle `(beta_(1))` and come to ground state by either emiting one `gamma`- ray (` gamma_(1)`) or emitting two `gamma`- rays (`gamma_(3)` and `gamma_(4)`) (ii) It can emit one `beta`- particle `(beta_(2))` and come to ground state by emitting `gamma_(2)` ray. Atomic masses: `""^(198)Au=197.9652` amu and `""^(198)Hg=197.9662` amu. Given that 1 amu= `930MeV//c^(2)`. The energy levels of the nucleus are shown in figure below
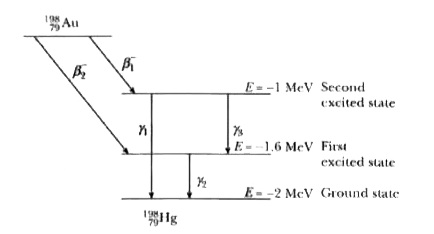
What is the maximum kinetic energy of emitted `beta_(1)` parricle ?
View SolutionGold nucleus `(""_(79)^(198)Au)` can decay into mercuyr nucleus `(""_(80)^(198)Hg^(8))` by two decay schemes shown in figure below (i) it can emit a `beta` -particle `(beta_(1))` and come to ground state by either emiting one `gamma`- ray (` gamma_(1)`) or emitting two `gamma`- rays (`gamma_(3)` and `gamma_(4)`) (ii) It can emit one `beta`- particle `(beta_(2))` and come to ground state by emitting `gamma_(2)` ray. Atomic masses: `""^(198)Au=197.9652` amu and `""^(198)Hg=197.9662` amu. Given that 1 amu= `930MeV//c^(2)`. The energy levels of the nucleus are shown in figure below
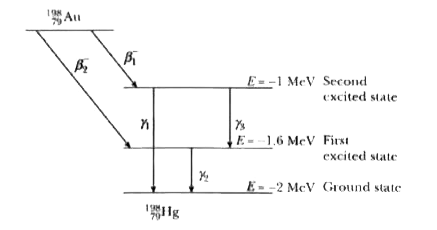
The wavelength of emitted `gamma` - rays is the order
View SolutionWe have two radioactive nuclei `A` and `B`. Both convert into a stable nucleus `C`. Nucleus `A` converts into `C` after emitting two two `alpha`-particles and three `beta`-particles. Nucleus `B` converts into `C` after emitting one.
`alpha`-particle anf five `beta`-particles. A time `t = 0`, nuclei of `A` are `4N_(0)` and that of `B` are `N_(0)`. Half-life of `A`(into the conversion of `C`) is `1min` and that of `B` is `2min`. Initially number of nuclei of `C` are zero.
If atomic numbers and mass numbers of `A` and `B` are `Z_(1),Z_(2),A_(1)` and `A_(2)` respectively. Then
View SolutionWe have two radioactive nuclei `A` and `B`. Both convert into a stable nucleus `C`. Nucleus `A` converts into `C` after emitting two two `alpha`-particles and three `beta`-particles. Nucleus `B` converts into `C` after emitting one.
`alpha`-particle anf five `beta`-particles. A time `t = 0`, nuclei of `A` are `4N_(0)` and that of `B` are `N_(0)`. Half-life of `A`(into the conversion of `C`) is `1min` and that of `B` is `2min`. Initially number of nuclei of `C` are zero.
What are number of nuclei of `C`, when number of nuclei of `A` and `B` are equal ?
View SolutionWe have two radioactive nuclei `A` and `B`. Both convert into a stable nucleus `C`. Nucleus `A` converts into `C` after emitting two two `alpha`-particles and three `beta`-particles. Nucleus `B` converts into `C` after emitting one.
`alpha`-particle anf five `beta`-particles. A time `t = 0`, nuclei of `A` are `4N_(0)` and that of `B` are `N_(0)`. Half-life of `A`(into the conversion of `C`) is `1min` and that of `B` is `2min`. Initially number of nuclei of `C` are zero.
At what time rate of disintergrations of `A` and `B` are equal.
View SolutionIn a nuclear fusion reactor, the reaction occurs in two stages (i) Two deuterium `(""_(1)^(2)D)` nuclei fuse to form a tritium `(""_(1)^(3)T)` nucleus with a proton as a byproduct. The reaction may be represented as D (D,p) T. (ii) A tritium nucleus fuses with another deuterium nucleus to form a helium `(""_(2)^(4)He)` nucleus with a neutron as a byproduct. The reaction is represented as `T(D.n)alpha`. Given that `m(""_(1)^(2)d)=2.014104u` (atom)
`m(""_(1)^(3)T)=3.01609u` (atom)
The energy released in 1st stage of fusion reaction is
View SolutionIn a nuclear fusion reactor, the reaction occurs in two stages (i) Two deuterium `(""_(1)^(2)D)` nuclei fuse to form a tritium `(""_(1)^(3)T)` nucleus with a proton as a byproduct. The reaction may be represented as D (D,p) T. (ii) A tritium nucleus fuses with another deuterium nucleus to form a helium `(""_(2)^(4)He)` nucleus with a neutron as a byproduct. The reaction is represented as `T(D.n)alpha`. Given that `m(""_(1)^(2)d)=2.014104u` (atom)
`m(""_(1)^(3)T)=3.01609u` (atom)
The energy released in the second stage of fusion reaction
View SolutionIn a nuclear fusion reactor, the reaction occurs in two stages (i) Two deuterium `(""_(1)^(2)D)` nuclei fuse to form a tritium `(""_(1)^(3)T)` nucleus with a proton as a byproduct. The reaction may be represented as D (D,p) T. (ii) A tritium nucleus fuses with another deuterium nucleus to form a helium `(""_(2)^(4)He)` nucleus with a neutron as a byproduct. The reaction is represented as `T(D.n)alpha`. Given that `m(""_(1)^(2)d)=2.014104u` (atom)
`m(""_(1)^(3)T)=3.01609u` (atom)
What percentage of the mass energy of the initial deuterium is released?
View SolutionConsider the following nuclear decay: `""_(92)^(236)Uto""_(90)^(232)Th+X`
What is X?
View SolutionConsider the following nuclear decay: `""_(92)^(236)Uto""_(90)^(234)Th+X`
Determine the amount of energy released in this decay. Use the following atomic masses.
`""_(92)^(236)=236.045562u, ""_(90)^(232)Th=232.038054u`
`""_(2)^(4)He=4.002603u, ""_(0)^(1)n=1.008665u` and `""_(1)^(1)p=1.007277h`
Conversion factors `1u=931.5meV, 1eV=1.602xx10^(-19)J`
View SolutionConsider the following nuclear decay: `""_(92)^(236)Uto""_(90)^(234)Th+X`
If the uranium is at rest before its decay, which one of the following statements is true concerning the final nuclei?
View Solution
PRACTICE QUESTIONS (Linked Comprehension) questions and complete solutions for chapter THE NUCLEUS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12