Complete Solutions to SAMPLE PROBLEM of chapter THE NUCLEUS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THE NUCLEUS |
| RESNICK AND HALLIDAY | SAMPLE PROBLEM |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
An alpha particle with kinetic energy `K_(i)=5.30` MeV happens, by chance,to be headed directly toward he nucleus of a neutral gold atom (fig). What is its distance of closest approach d (least center to center separation) to the nucleus? Assume that the atom remains stationary.
View SolutionWhat is the binding energy per nucleon for `""^(120)Sn`?
View SolutionThe table that follows shows some measurements of the decay rate of a sample of `.^(128)I`, a radio nuclide often used medically as a tracer to measure the rate at which iodine is absorbed by the thyroid gland.
`|{:("Time(min)",A (counts//s),"Time(min)",A(counts)//s,),(4,392.2,132,10.9,),(36,161.4,164,4.56,),(68,65.5,196,1.86,),(10,26.8,218,1.00,):}|`
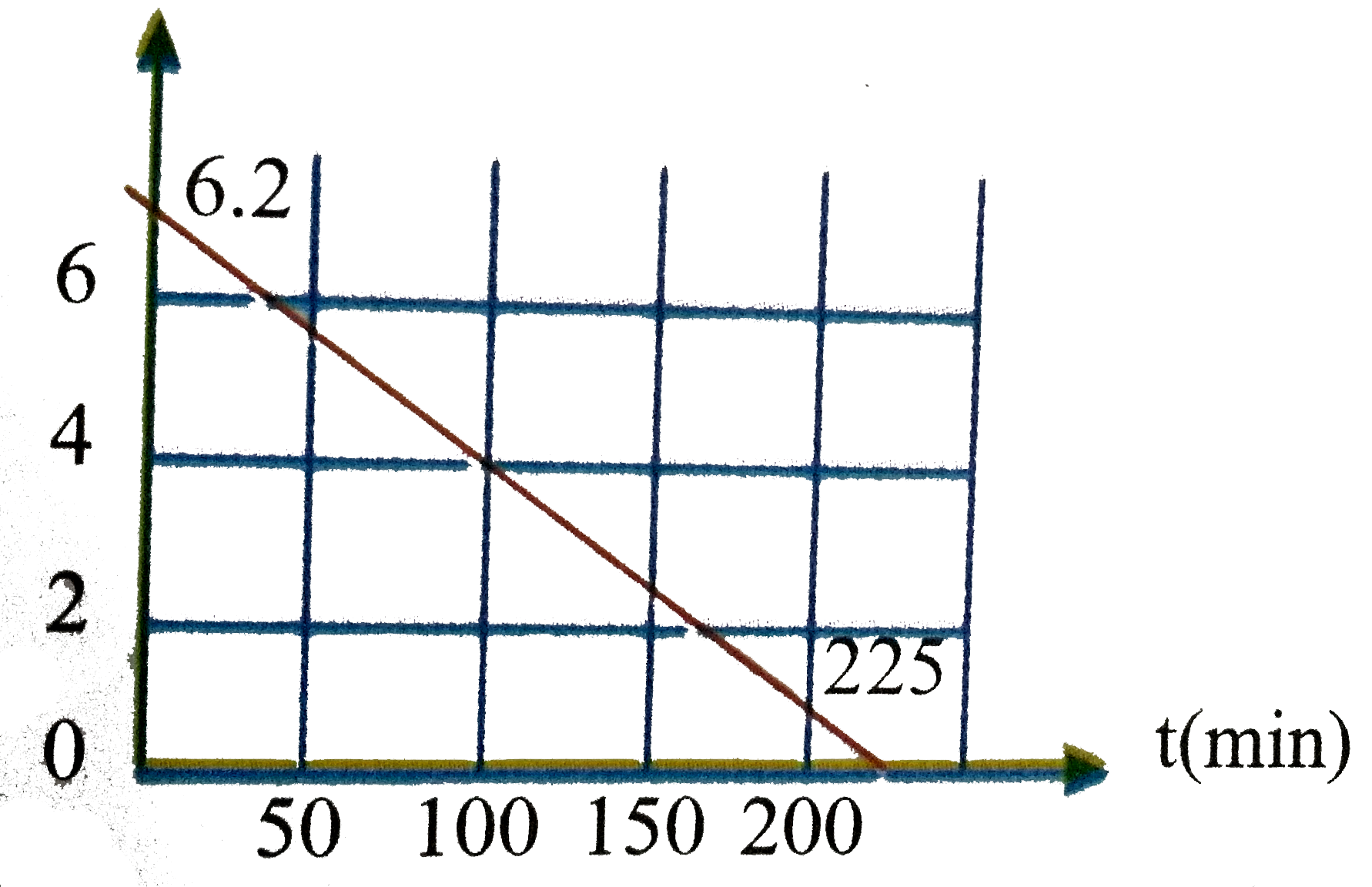
The half life `t_(1//2)` for this radio nuclide.
View SolutionIiodine -131 is a radioactive isdotpe. If 1.0 mg of `""^(131)I` has an activity of `4.6xx10""^(12)`Bq. What is the half-life of `""^(131)I` (in days)
View SolutionA sample contains large number of nuclei. The probability that a nucleus in sample will decay after four half lives is
View SolutionWe are given the following atomic masses :
`._(92)^(238)U = 238.05079 u " " ._(2)^(4)He=4.00260 u`
`._(90)^(234)Th=234.04363u " " ._(1)^(1)H=1.00783 u`
`._(91)^(237)Pa=237.05121 u`
Here the symbol Pa is for the element protactinium (Z = 91) .
Calculate the energy released during the alpha decay of `._(92)^(238)U`.
View SolutionCalculate the disintegeration energy Q for the beta decay of `""^(32)P,` . The needed atomic masses are 31.973 u of `""^(32)P` and 31.972 u for `""^(32)S`
View SolutionIn a Moon rock sample the ratio of number of (stable) `""^(40)Ar` atoms present to the number of (radioactive)`""^(40)K` atoms is 10.3. Assume that all the argon atoms were produced by the decay of potassium atoms, with a half life of `1.25xx10^(9)y`. How old is the rock?
View SolutionConsider the neutron capture reaction
`""^(109)Ag+nto""^(110)Agto""^(110)Ag+gamma` (40-34)
in which a compound nucleus `(""^(110)Ag)` is formed. Figure 40-18 shows the relative rate at which such events take place, plotted against the energy of the incoming neutron. Find the mean lifetime of this compound nucleus by using the uncertainty principle in the form
`DeltaE.Deltat~~hath`. (40-35)
here `DeltaE` is a mesure of the uncertainty with which the energy of a state can be defined. The quantity `Deltat` is a measure of the time available of measure this energy. In fact here `Deltat` is just `t_("avg")`, the average life of the compound nucleus befoe it decays to its ground state.
Reasoning: We see that the relative reaction rate peaks sharply at a neutron energy of about 5.2 eV.This suggests that we are dealing with a single excited energy level of the compund nucleus `""^(110)Ag`. When the availabel energy(of the incoming neutron) just matches the energy of this level above the neutron) just matches the energy of this level above the `""^(110)Ag` ground state, we have resonance and the reaction of Eq. 40 -34 really goes.
However, the resonance peak is not infinitely sharp but has an approximate half peak is not infinitely shart but has an approximate half width (`DeltaE` in the figue) of about 0.20 eV. We can account for this resonance peak width by saying that the excited level is not sharply defined in energy but has an energy uncertainty `DeltaE` of about 0.20 eV.
Calculation : Subsitiuting that uncertainty of 0.20 2V into Eq. given us
`Delta = t_(avg) ~~ h/(DeltaE) ~~ ((4.14 xx 10^(-15) eV.s)//2pi)/(0.20 eV)`
`~~ 3 xx 10^(-15) s`.
This is several hundraed times greater than the time a 5.2 eV neutron takes to cross the diameter of a `""^(109)Ag` nucleus . Therefore , the neutron is spending this time of `3xx 10^(-15)` s as part of the nucleus.
View SolutionConsider the fission of `._(92)^(238)U` by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primay fragments, are `._(58)^(140)Ce` and `._(44)^(99)Ru`. Calculate Q for this fission process. The relevant atomic and particle masses are
`m(._(92)^(238)U)=238.05079 u`
`m(._(58)^(140)Ce)=139.90543 u`
`m(._(44)^(99)Ru)=98.90594 u`
View SolutionAssume a proton is a sphere of radius `R~~1` fm. Two protons are fired at each other with the same kinetic energy. K
a. What must K be if the paticles are brought to rest by their mutual Coulomb repulsion when they are just touching each other? We can take this value of K as a representative measure of the height of the Colulomb barrier.
View SolutionTemperature of an ideal 'gas whose molecules have average kinetic energy 1 e V is
View Solution
SAMPLE PROBLEM questions and complete solutions for chapter THE NUCLEUS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12