Complete Solutions to Exercise 11A of chapter APPLICATIONS OF DERIVATIVES of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATIONS OF DERIVATIVES |
| RS AGGARWAL | Exercise 11A |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
The side of a square in increasing at the rate of 0.2 cm/sec. Find the rate of increase of the perimeter of the square.
View SolutionThe radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
View SolutionThe radius of a circle is increasing uniformly at the rate of 0.3 centimetre per second. At what rate is the area increasing when the radius is 10 cm ? (Take `pi = 3.14`)
View SolutionThe side of a square sheet of metal is increasing at 3 centimetres per minute. At what rate is the area increasing when the side is 10 cm long ?
View SolutionThe radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
View SolutionThe radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
View SolutionThe volume of a spherical balloon is increasing at a rate of ` 25 cm^(3)//sec`. Find the rate of increase of its curved surface when the radius of balloon is 5 cm.
View SolutionA balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
View SolutionThe bottom of a rectangular swimming tank is 25 m by 40m. Water is pumped into the tank at the rate of 500 cubic metres per minute. Find the rate at which the level of water in the tank is rising.
View SolutionA stone is dropped into a quiet lake and waves move in circles at a speed of 3.5 cm per second. At the instant when the radius of the circular wave is 7.5 cm, how fast is the enclosed area increasing ? (Take `pi = 22//7`)
View SolutionA man 2 metres high walks at a uniform speed of 5 km/hr away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.
View SolutionAn inverted cone has a depth of 40 cm and a base of radius 5 cm. Water is poured into it at a rate of 1.5 cubic centimetres per minutes. Find the rate at which the level of water in the cone is rising when the depth is 4 cm
View SolutionSand is pouring from a pipe at the rate of `18 cm^(3)//s`. The falling sand forms a cone on the ground in such a way that the height of the cone is one-sixth of the radius of the base. How fast is the height of the sand cone increasing when its height is 3 cm?
View SolutionWater is dripping out from a conical funnel at a uniform rate of `4c m^3//c m` through a tiny hole at the vertex in the bottom. When the slant height of the water is 3cm, find the rate of decrease of the slant height of the water-cone. Given that the vertical angle of the funnel is `120^0dot`
View SolutionOil is leaking at the rate of 16 mL/s from a vertically kept cylindrical drum containing oil. If the radius of the drum is 7 cm and its height is 60 cm, find the rate at which the level of the oil is changing when the oil level is 18 cm
View SolutionA 13-m long ladder is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 m/s. How fast is its height on the wall decreasing when the foot of the ladder is 5m aways from the wall ?
View SolutionA man is moving away from a 40-m high tower at a speed of 2 m/s. Find the rate at which the angle of elevation of the top of the tower is changing when he is at a distance of 30 metres from the foot of the tower. Assume that the eye level of the man is 1.6 m from the ground.
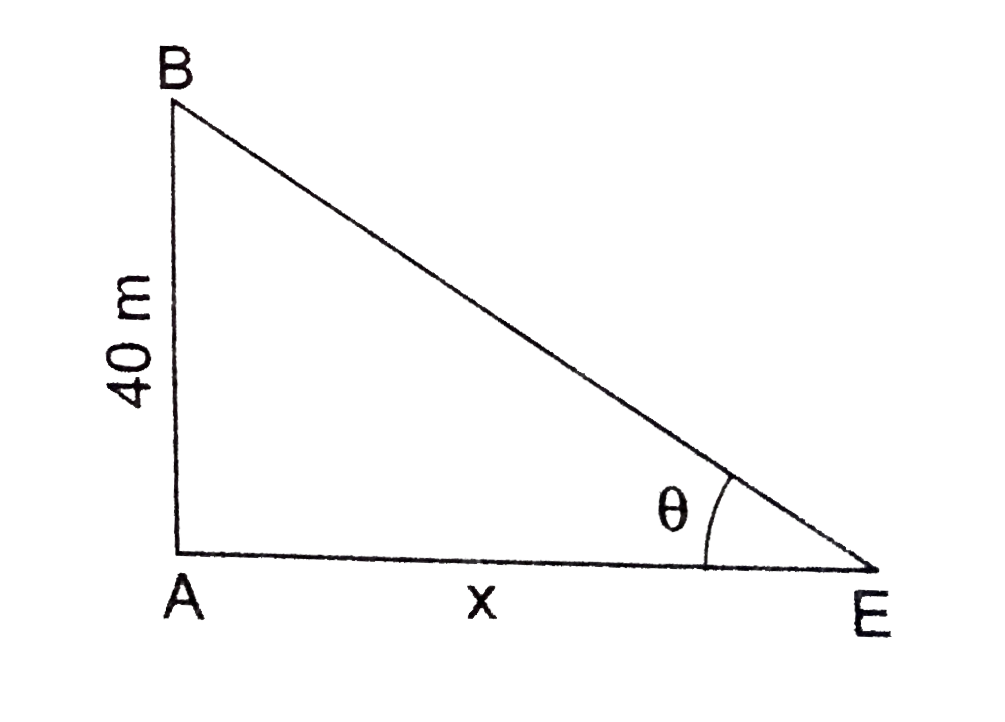
View SolutionFind an angle `theta,0
View SolutionThe radius of a balloon is increasing at the rate of 10 cm/sec. At what rate is the surface area of the balloon increasing when the radius is 15 cm?
View SolutionAn edge of a variable cube is increasing at the rate of 5 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long ?
View SolutionThe sides of an equilateral triangle are increasing at the rate of 2 cm/sec. Find the rate at which the area increases, when the side is 10 cm.
View Solution
Exercise 11A questions and complete solutions for chapter APPLICATIONS OF DERIVATIVES of RS AGGARWAL MATHS (HINGLISH) of Class 12