Complete Solutions to Solved Examples of chapter LINEAR PROGRAMMING of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LINEAR PROGRAMMING |
| RS AGGARWAL | Solved Examples |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Graph the solution set of the inequatin `2x -yge1.`
View SolutionDraw the graph of the solution set of the system of inequations `2x+3yle 4, xge0and y ge 0.`
View SolutionExhibit graphically the solution set of the system of lineear inequations `x+yge1,7x+9yle63,y le5,xle6,x ge0andyge0.`
View SolutionFind the linear constraints for which the shaded area in the figure below is the solution set.

View SolutionSolve the following problem graphically :
Minimise and Maximise `Z = 3x + 9y` . . . (1)
subject to the constraints: `x+3ylt=60` . . . (2)
`x+ygeq10` . . . (3)
`xlt=y` . . . (4)
`xgeq0,ygeq0` . . . (5)
View SolutionA faniture dealer deals in only two itmes - tables and chairs. He has 'Rs. 50000 invest and has storage place of at most 60 pieces. A table costs Rs. 2500 and chair Rs. 500. He estimates that from the sale of one table, he can make a perfect Rs. 250 and that from the sale of one chair a profit of Rs. 75. How many table and chair he should buy from the available money so as to maximise his total profit assuming that he can sell all the items which he buys.
View SolutionIf a young man rides his motorcycle at 25 km/hr, he has to spend 2 per kilometer on petrol if per he rides it at a faster speed of 40 km/hr the petrol cost increases to 5 per kilometer.He has 100 to spend on petrol and wishes to find the maximum distance he can travel within one hours. Express this as a linear programming problem and then solve it.
View SolutionSuppose every gram of wheat provides 0.1 g of proteins and 0.25 g of carbohydrates, and the corresponding values for rice are 0.05 g and 0.5 g respectively. Wheat costs Rs.5 and rise Rs.20 per kilogram. The minimum daily requirements of proteins and carbohydrates for an average man are 50 g and 200 g respectively. In what quantities should wheat and rice be mixed in hte daily diet to provide the minimum daily requirements of proteins and carbohydrates at minimum daily requirements of proteins and carbohydrates at minimum cost, assuming that both wheat and rice are to be taken in the diet?
View SolutionA firm manufactures two types of products, A and B, and sells them at a profil of 3 per unit to type B product and 5 perunit of type A product. Both product is processed on two machines M1and M2 One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2i whereas one unit of type B requires one minute of processing time on M1 and one minute on M Machines sells them at a profit of 5 per unit of type A and M, and M, are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product the firn should produce a day in order to maximize the profit. Solve the problem graphically [CHSE 2000]
View SolutionAn aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
View SolutionA chemicla industry produces two compounds, A and B. The following table gives the units of ingredients C and D (per kg) of compounds A and B as well as minimum requirements of C and D, and costs per kg of A and B.

Find the quantities of A and B which would minimize the cost.
View SolutionA company makes two kinds of leather belts, A and B. Belt A is high quality belt, and B is of lower quality. The respective profits are Rs. 40 and Rs. 30 per belt. Each belt of type A requires twice as much time as a belt of type B, and if all belts were of type B, the company could make 1000 belts per day. The supply of leather is sufficient for only 800 belts per day (both A and B combined). Belt A requires a fancy buckle, and only 400 buckles per day are available. There are only 700 buckles available for belt B. What should be the daily production of each type f belt? Formulate the problem as a LPP.
View SolutionA company has factories located at each of the two places P and Q. From these locations, a certain commondity is delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 7, 6 and 4 units of the commodity while the weekly production capacities of the factories at P and Q are respectively 9 and 8 units. The cost of transportation per unit is given below.
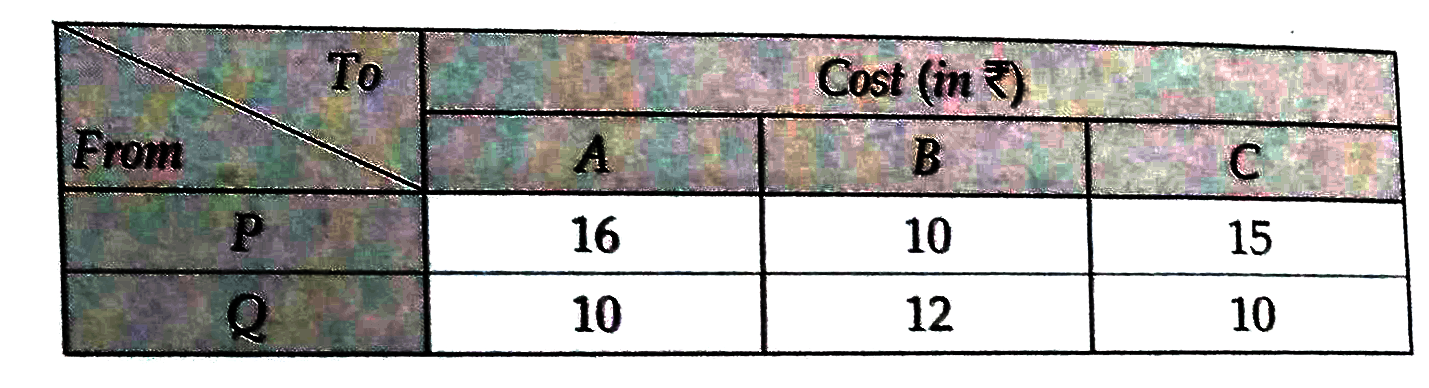
How many units should be transported from each factory to each depot in order that the tranporatin cost is minimum ? formulate the above LPP mathematically and then slove it.
View SolutionA factory owner purchase two types of machines A and B for his factory. The requirements and the limitations for the machines are as follows :

He has maximum area of `9000m^(2)` available and 72 skilled laborer's who can operate both the machines. How many machines of each type should he buy to maximize the daily output ?
View SolutionA retired person has Rs 70,000 to invest and two types of bonds are available in the in the market investment. First type of bond yields an annual income of 8% on the amount investment invested and second type of bond yields 10% per annum. As per norms, he has to invest minimum in the first type and not more than 30,000 in the second type. How should investment, so as to get maximum returns, after one year of investment?
View Solution
Solved Examples questions and complete solutions for chapter LINEAR PROGRAMMING of RS AGGARWAL MATHS (HINGLISH) of Class 12