Complete Solutions to इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए of chapter विद्युत् विभव तथा धारिता of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | विद्युत् विभव तथा धारिता |
| SHIVLAAL PUBLICATION | इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
संलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
`V_(P)-V_(Q)` तथा `V_(B)-V_(A)`

View Solutionसंलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
एक अल्प ऋणावेश के लिए `U_(Q)-U_(P)` तथा `U_(A) -U_(B)`

View Solutionसंलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
एक अल्प धनावेश के लिए `W_(QrarrP)` तथा `W_(BrarrA)`

View Solutionसंलग्न चित्र 2.74 (a) में धनावेश तथा चित्र 2.74 (b) में ऋणावेश के कारण विद्युत् क्षेत्र रेखाएँ प्रदर्शित हैं। बताइए कि निम्नलिखित में से कौन-सी राशि धनात्मक होगी तथा कौन-सी ऋणात्मक ?
एक अल्प ऋणावेश के लिए `(K.E)_(A) - (K.E)_(B)`

View Solutionनिम्नलिखित दशाओं में समविभव पृष्ठ क्या होंगे ?
Z दिशा में एक नियत विद्युत् क्षेत्र
View Solutionनिम्नलिखित दशाओं में समविभव पृष्ठ क्या होंगे ?
Z दिशा में एकसमान दर से बढ़ता हुआ एक विद्युत् क्षेत्र
View Solutionनिम्नलिखित दशाओं में समविभव पृष्ठ क्या होंगे ?
मूल बिन्दु पर स्थित बिन्दु आवेश।
View Solutionसंलग्न चित्र 2.75 में एक आवेश + q, वृत्त के केन्द्र पर रखा है। एक अन्य आवेश + q' को वृत्त की परिधि पर A से B तक ले जाने में कितना कार्य करना पड़ेगा ?
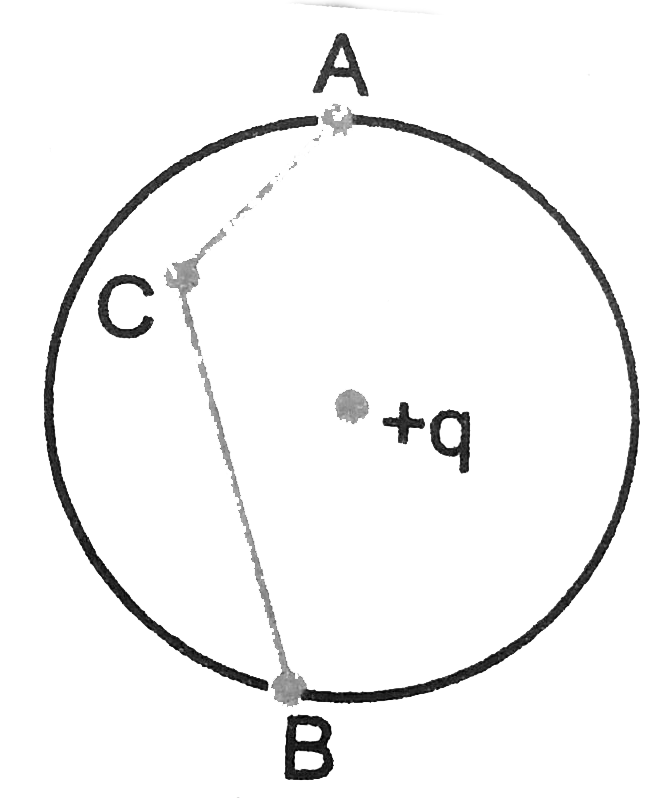
View Solutionसंलग्न चित्र 2.75 में एक आवेश + q, वृत्त के केन्द्र पर रखा है। एक अन्य आवेश + q' को पहले A से C तक तथा फिर C से B तक ले जाने में किस मार्ग में कार्य अधिक करना होगा ?

View Solutionक्या कारण है कि उच्च आवेश से आवेशित एक खोखले गोलीय चालक के अन्दर व्यक्ति झटके का अनुभव नहीं करता है ?
View Solutionविद्युत् क्षेत्र रेखाओं के अनुदिश विभव बढता है अथवा घटता है ? कारण सहित उत्तर दीजिए।
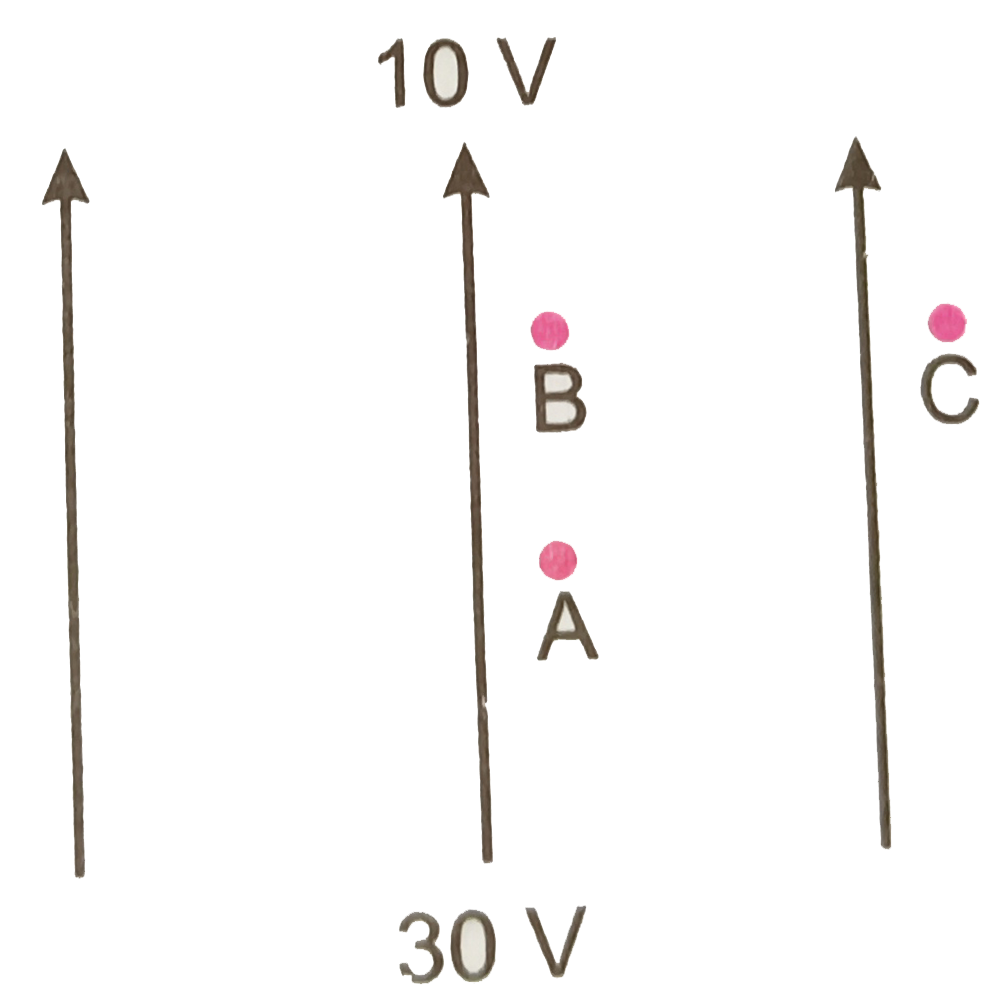
View Solutionसंलग्न चित्र 2.76 में कुछ समविभव पृष्ठ प्रदर्शित हैं तथा उनके विभव कोष्ठक में दिये गये हैं। A, B तथा C में से किस बिन्दु पर विद्युत् क्षेत्र का तीव्रता सबसे अधिक है ?
View Solutionएक घन की प्रत्येक कोर a है तथा इसके प्रत्येक शीर्ष पर आवेश q है। घन के केन्द्र पर विद्युत् विभव की गणना कीजिए।
View Solutionयदि `vecE = 2xhati -yhati + z^(2)hatk` तो बिन्दु (1, 1, 1) पर विभव ज्ञात कीजिए।
View Solutionयदि V = 2x +3y-5z वोल्ट है तो `vecE` ज्ञात कीजिए।
View Solutionकथन 1 : बिन्दु P से बिन्दु Q तक एक आवेशित कण को ले जाने में विद्युत् क्षेत्र द्वारा कण पर किया गया कार्य, बिन्दु P को बिन्दु Q से जोड़ने वाले मार्ग पर निर्भर नहीं करता है।
कथन 2 : एक वस्तु को बन्द लूप के अनुदिश ले जाने में संरक्षी बल द्वारा किया गया कार्य शुन्य होता है।
View Solutionविभव की विमा समान होती है :
View Solutionचित्र 2.77 में कुछ समविभव क्षेत्र दर्शाये गये हैं :

एक धनात्मक आवेश q को A से B तक प्रत्येक आरेख से ले जाते हैं तो-
View Solutionएक वर्ग की भुजा 93 मीटर है। इसके तीन कोनों पर आवेश क्रमशः `q_(1)` = 33 नैनो-कूलॉम, `q_(2)` =-51 नैनो-कूलॉम तथा `q_(3)` = 47 नेनो-कूलॉम रखे हैं। वर्ग के चौथे कोने पर विभव होगा :
View Solutionएक इलेक्ट्रॉन निम्न विभव क्षेत्र `V_(1)` से चलते हुए एक उच्च विभव क्षेत्र `V_(2)` से गुजरता है। उच्च विभव क्षेत्र में इसके वेग में :
View Solutionचित्र 2.78 के अनुसार आवेश + q तथा - q एक समद्विबाहु त्रिभुज के शीर्षों B तथा C पर रखे गये हैं। शीर्ष A पर विभव का मान है :

View Solutionएक आवेश (-q) तथा दूसरा आवेश (+ Q) क्रमशः दो बिन्दुओं A व B पर रखे जाते हैं। आवेश (+Q) को बिन्दु B पर स्थिर रखकर, बिन्दु A पर रखे आवेश (-q) को एक अन्य बिन्दु C पर ले जाते हैं ताकि ABC एक समबाहु त्रिभुज बनता है जिसकी प्रत्येक भुजा की लम्बाई l है। आवेश (-q) को चलाने में किया गया कुल कार्य होगा :
View Solutionयदि किसी बिन्दु पर विद्युत् विभव V है तो X-अक्ष के अनुदिश उस बिन्दु पर विद्युत क्षेत्र होगा :
View Solutionचित्र 2.79 में लम्बाई L की छड़ AB पर आवेश Q एकसमान रूप से वितरित है। सिरे A से दूरी L पर स्थित बिन्दु O पर विद्युत् विभव होगाः

View Solutionयदि किसी क्षेत्र में विभव (वोल्ट में) को `V_((x,y,z))=6xy-y+2yz` से व्यक्त किया जाए तो, बिन्दु (1, 1, 0) पर विद्युत् क्षेत्र (N/C में) है :
View Solutionकिसी क्षेत्र में विद्युत् विभव `V_((x,y,z) = 6x-8xy-8y + 6yz` वोल्ट है, जहाँ x, y, z मीटर में हैं। बिन्दु (1, 1, 1) पर रखे 2 कूलॉम आवेश पर लगने वाला विद्युत् बल होगा :
View SolutionX-अक्ष पर स्थित कुछ आवेशों के कारण किसी बिन्दु पर विभव `V((x))=20/(x^(2)-4)` वोल्ट है, जहाँ x माइक्रो-मीटर में है। `x=4mum` पर विद्युत् क्षेत्र `vecE` होगा :
View Solutionएक विद्युत् क्षेत्र `vecE = 30x^(2)hati` में x = 0 पर विभव `V_(0)` तथा x = 2 मीटर पर विभव `V_(A)` के लिए `V_(A)-V_(0)` का मान होगा :
View Solutionएक एकसमान विद्युत् क्षेत्र में रखे जाने पर आवेश 3 कूलॉम पर बल 300 न्यूटन लगता है तो विद्युत् क्षेत्र रेखाओं की दिशा में 1 सेमी दूरी पर स्थित दो बिन्दुओं के बीच विभवान्तर होगा :
View Solutionत्रिज्याओं r तथा R (R`gt`r) के संकेन्द्रिक खोखले गोलों पर कोई आवेश Q इस प्रकार वितरित है कि उनके पृष्ठ घनत्व समान हैं। उनके उभयनिष्ठ केन्द्र पर विभव है :
View Solutionएक विद्युत् आवेश `10^(-3)muC` को X-Y निर्देशांक पद्धति के मूल बिन्दु (0, 0) पर रखा जाता है। दो बिन्दु A तथा B क्रमशः `(sqrt2,sqrt2)` मीटर तथा (2, 0) मीटर पर स्थित हैं। A तथा B बिन्दुओं के बीच विभवान्तर होगा :
View Solutionदो बिन्दु आवेशों 100 `muC` और `5muC` को क्रमशः A और B बिन्दुओं पर रखा गया है, जहाँ AB = 40 सेमी है। बाह्य बल द्वारा आवेश `5muC` को B से C तक विस्थापित करने में किया गया कार्य होगा
: (जहाँ BC = 30 सेमी, कोण ABC = `(pi)/2`)
View Solutionदो समान एवं विपरीत आवेश (+ q तथा - q) एक-दूसरे से दूरी l पर स्थित हैं। इस निकाय के कारण, किसी स्थित बिन्दु पर विभव का मान निर्भर करेगा :
View Solutionएक विद्युत् द्विध्रुव से r दूरी पर स्थित किसी बिन्दु पर विद्युत् विभव अनुक्रमानुपाती होता है :
View Solutionएक विद्युत् द्विध्रुव की अक्ष के किसी बिन्दु पर :
View Solutionयदि विद्युत् द्विश्रुव के आवेशों के बीच की दूरी l है तो द्विथ्रुव के मध्य बिन्दु पर विद्युत् क्षेत्र एवं विभव का अनुपात (E/V) का मान होगा :
View Solutionद्विध्रुव आघूर्ण p वाले छोटे द्विध्रुव के निरक्षीय स्थिति पर द्विध्रुव से दूरी r पर विद्युत् विभव होता है :
View SolutionHCl अणु में `H^(+)` तथा `Cl^(-)` आयनों के बीच की दूरी 1.28 Å है। इस द्विध्रुव के कारण इसकी अक्ष पर दूरी 12 Å पर विभव होगा :
View Solutionदो समान, किन्तु विपरीत आवेश q जिनके बीच की दूरी 2a है, एक वैद्युत द्विध्रुव बनाते हैं जिसका द्विध्रुव आघूर्ण p है। वैद्युत द्विध्रुव के मध्य से दूरी r पर एक बिन्दु P को जोड़ने वाली रेखा वैद्युत द्विध्रुव की अक्ष से कोण `theta` बनाती है। बिन्दु P पर विभव होगा `(rgtgt2a)` (जहाँ p = 2qa) :
View Solutionकिसी विद्युत् द्विध्रुव के कारण किसी बिन्दु पर विद्युत् विभव होता है :
View Solutionदूरी 2a पर दो समान आवेश q रखे हुए हैं और तीसरा आवेश - 2q उनके मध्य बिन्दु पर रखा जाता है। इस निकाय की स्थितिज ऊर्जा होगी :
View Solutionतीन आवेश Q, (+ q) एवं (+ q) एक समबाहु त्रिभुज, जिसकी भुजाओं की लम्बाई l है, के शीर्ष बिन्दुओं पर स्थित हैं (चित्र 2.80) । यदि इस निकाय की कुल स्थिर- वैद्युत ऊर्जा शून्य हो, तो Q का मान होगा:

View Solutionभुजा 2a के एक वर्ग ABCD की एक भुजा AB के सिरों पर दो धनात्मक आवेश q परिमाण के रखे गये हैं। उसी परिमाण के दो ऋणात्मक आवेश शेष दोनों कोनों पर रखे गये हैं। विराम अवस्था से प्रारम्भ करके यदि एक आवेश Q भुजा AB के मध्य -बिन्दु से वर्ग के केन्द्र की ओर चलता है तो वर्ग के केन्द्र पर इसकी गतिज ऊर्जा होगी :
View Solutionचित्र 2.81 के अनुसार एक वर्ग के कोनों पर आवेश रखे हैं। यदि केन्द्र पर विद्युत् क्षेत्र `vecE` तथा विभव V है तो कोनों A व B के आवेशों को क्रमशः कोनों D व C से आपस में बदलने परः

View Solutionसही सम्बन्ध है :
View Solutionसमविभव पृष्ठ तथा विद्युत् क्षेत्र रेखाओं के बीच कोण होता है :
View Solutionएकसमान आवेशित त्रिज्या a के गोले के बाहर उससे दूरी r पर विद्युत् विभव होता है :
View Solutionआवेश Q से आवेशित त्रिज्या R के चालक गोले के अन्दर केन्द्र से दूरी x पर विद्युत् विभव होता है :
View Solutionत्रिज्या 10 सेमी वाले एक विलगित गोले को विभव V तक आवेशित किया जाता है जिससे इसका पृष्ठ घनत्व 1 माइक्रो-कूलॉम/मीट`र^(2)` हो जाता है। V का मान है :
View Solutionत्रिज्या 5 सेमी के धातु के एक खोखले गोले को इस प्रकार आवेशित किया जाता है कि उसकी सतह पर विभव 10 वोल्ट हो जाता है। गोले के केन्द्र पर विभव होगा :
View Solutionत्रिज्या 1.0 मीटर के एक आवेशित खोखले गोलीय चालक के पृष्ठ पर विभव 1000 वोल्ट है। इसके केन्द्र से 0.25 मीटर दूरी पर विभव होगा :
View Solutionएक आवेशित गोलीय गेंद के अन्दर विद्युत् विभव `V = ar^(2) + b` है, जहाँ r केन्द्र से दूरी है तथा a व b नियतांक हैं। गेंद के अन्दर आवेश घनत्व होगा :
View Solutionत्रिज्या 5 सेमी के धातु के एक खोखले गोले को इस प्रकार आवेशित किया जाता है कि उसकी सतह पर विभव 10 वोल्ट हो जाता है। गोले के केन्द्र पर विद्युत् क्षेत्र का मान होगा :
View Solutionत्रिज्या R के एक चालक गोले को आवेश Q दिया जाता है। गोले के केन्द्र पर विद्युत् विभव तथा विद्युत् क्षेत्र क्रमशः होंगे :
View Solutionत्रिज्या R के एक कुचालक ठोस गोले पर एकसमान आवेश घनत्व p है जिसके कारण इसके केन्द्र पर अन्दर, सतह पर तथा बाहर विद्युत् विभव परिमिति है अनन्त पर विद्युत् विभव शुन्य है।
कथन 1 : केन्द्र से सतह तक आवेश q को ले जाने में स्थितिज ऊर्जा में अन्तर `qp//3epsilon_(0)`, होता है।
कथन 2 : गोले के केन्द्र से दूरी r पर (r `lt` R) विद्युत् क्षेत्र `pr//3epsilon_(0)`, होता है।
View Solutionत्रिज्या r के वृत्त की परिधि पर, जिसके केन्द्र पर आवेश Q है, आवेश Q' को घुमाने में किया गया कार्य होता है :
View Solutionदो बिन्दुओं P तथा Q पर विभवे क्रमशः 10 V तथा - 4 V है। 100 इलेक्ट्रॉनों को P से Q तक ले जाने में किया गया कार्य होगा :
View Solutionसंलग्न चित्र 2.82 में एकसमान रूप से आवेशित अनन्त लम्बाई की दो विद्युतुरोधी पटिकाओं के बीच विभवान्तर `V_(2)-V_(1)` = 20 वोल्ट है तथा इनके बीच की दूरी 0.1 मीटर है। यदि पट्टिका 1 के अन्दर की सतह से एक इलेक्ट्रॉन विराम अवस्था से छोड़ा जाता है तो पट्टिका 2 पर टकराते समय इलेक्ट्रॉन की चाल होगी :

View Solutionएक इलेक्ट्रॉन विभवान्तर 200 वोल्ट द्वारा त्वरित किया जाता है। यदि इलेक्ट्रॉन के लिए विशिष्ट आवेश e/m का मान `1.6 xx 10^(11)` कूलॉम प्रति किग्रा हो तो इलेक्ट्रॉन द्वारा अर्जित वेग होगा :
View Solutionइलेक्ट्रॉन वोल्ट मात्रक है :
View Solutionमिलिकॉन की तेल बूँद विधि के एक प्रयोग में आवेश Q के तेल की एक बूँद को विभवान्तर 2400 वोल्ट पर रखी दोनों प्लेटों के बीच स्थिर रखा जाता है। इस बूँद की आधी त्रिज्या की एक अन्य बूँद को स्थिर रखने के लिए विभवान्तर 600 वोल्ट की आवश्यकता होती है। तब इस दूसरी बूँद पर आवेश होगा :
View Solutionचित्र 2.83 में त्रिज्या a तथा b के दो समकेन्द्री गोलों के बीच के स्थान में आयतन आवेश-घनत्व `p = A/r` है, जहाँ A नियतांक है तथा r केन्द्र से दूरी है। गोलों के केन्द्र पर एक बिन्दु-आवेश Q है। यदि गोलों के बीच के स्थान में विद्युत् क्षेत्र एकसमान है, तो A का मान होगा :

View SolutionR त्रिज्या के किसी एकसमान आवेशित ठोस गोले के पृष्ठ का विभव `V_(0)` है (`oo` के सापेक्ष मापा गया)। इस गोले के लिए, `(3V_(0))/2,(5V_(0))/4,(3V_(0))/4` तथा `(V_(0))/4` विभवों वाले समविभवी पृष्ठों की त्रिज्याएँ, क्रमशः `R_(1), R_(2), R_(3)` तथा `R_(4)` हैं, तो
View Solutionधातु के घनाकार एक टुकड़े को धनात्मक आवेश Q दिया गया है। सत्य कथन है :
View Solutionविद्युत् क्षेत्र की तीव्रता E वाले स्थान पर इसके कारण ऊर्जा धनत्व का मान (निर्वात मे) होगा:
View Solutionसूर्य से आने वाले प्रकाश के विद्युत् क्षेत्र का वर्ग माध्य मूल मान 720 न्यूटन/कूलॉम है। विद्युत्-चुम्बकीय तरंग का माध्य सम्पूर्ण ऊर्जा घनत्व होगा :
View Solutionक्या कारण है कि संधारित्र में परावैद्युत माध्यम की रूप में किसी धातु की उपयोग में नहीं लाया जाता है ?
View Solutionदो एक-जैसे संधारित्र समान्तर क्रम में जुड़े हैं। इन्हें किसी निश्चित विभव तक आवेशित करके अलग कर लिया जाता है तथा फिर श्रेणीक्रम में जोड़ देते हैं। निम्नलिखित पर क्या प्रभाव पड़ेगा ?
संयोजन की कुल ऊर्जा
View Solutionदो एक-जैसे संधारित्र समान्तर क्रम में जुड़े हैं। इन्हें किसी निश्चित विभव तक आवेशित करके अलग कर लिया जाता है तथा फिर श्रेणीक्रम में जोड़ देते हैं। निम्नलिखित पर क्या प्रभाव पड़ेगा ?
विभवान्तर
View Solutionदो एक-जैसे संधारित्र समान्तर क्रम में जुड़े हैं। इन्हें किसी निश्चित विभव तक आवेशित करके अलग कर लिया जाता है तथा फिर श्रेणीक्रम में जोड़ देते हैं। निम्नलिखित पर क्या प्रभाव पड़ेगा ?
आवेश
View Solutionएक चालक पर कोई आवेश नहीं है क्या इसकी धारिता शुन्य होगी ?
View Solutionएक-जैसे n संधारित्र, जिनमें प्रत्येक की धारिता C है, समान्तर क्रम में जुड़े हैं। इन्हें विभव V तक आवेशित किया गया है। संयोजन का कुल आवेश, कुल विभवान्तर तथा ऊर्जा ज्ञात कीजिए। यदि इन्हें अलग- अलग करके श्रेणीक्रम में जोड़ दें तो आपके उत्तर पर क्या प्रभाव पड़ेगा ?
View Solutionनिम्नलिखित चित्र 2.87 में प्रत्येक संधारित्र की प्लेट का क्षेत्रफल A तथा प्लेटों के बीच की दूरी d है। प्रत्येक संधारित्र की धारिता ज्ञात कीजिए।

View Solutionएक समान्तर प्लेट संधारित्र (जिसकी प्रत्येक प्लेट का क्षेत्रफल A तथा प्लेटों के बीच की दूरी d है) के ठीक बीच में नगण्य मोटाई की धात्विक प्लेट को रखकर इसे संधारित्र की ऊपर की प्लेट से जोड़ दिया जाता है। संधारित्र की धारिता क्या होगी ?
View Solutionएक समान्तर प्लेट संधारित्र समान दूरी पर स्थित n प्लेटों से मिलकर बना है। इन प्लेटों को एकान्तर क्रम में जोड़ा गया है। यदि किन्हीं भी दो प्लेटों के बीच धारिता C है, तो संयोजन की कुल धारिता ज्ञात कीजिए।
View Solutionदो परिवर्ती संधारित्रों में से प्रत्येक की धारिता `10muF` से लेकर `100muF` तक बदली जा सकती है। इनको समूहित करके महत्तम तथा न्यूनतम कितनी धारिता प्राप्त की जा सकती है ?
View Solutionएक गोलीय चालक की धारिता का सूत्र है :
View Solutionयदि पृथ्वी का पृष्ठ क्षेत्रफल A तथा आयतन V है तो इसकी धारिता होगी :
View Solutionयदि किसी गोले की परिधि 2 मीटर है तो पानी (K = 80.4) में गोले की धारिता होगी :
View Solutionएक संधारित्र को विभवान्तर 200 वोल्ट द्वारा आवेशित किया जाता है तथा इस पर आवेश 1 कूलॉम है। जब इसे विसर्जित किया जाता है, तो इससे ऊर्जा मुक्त होगी :
View Solutionविद्युत्शीलता का मात्रक है :
View Solutionधारिता का विमीय सूत्र है :
View Solutionकिसी संधारित्र को एक बैटरी से आवेशित किया जाता है। फिर बैटरी को हटाकर, इस संधारित्र से, समान्तर क्रम में ठीक ऐसा ही एक अन्य अनावेशित संधारित्र जोड़ दिया जाता है तो, इस प्रकार बने परिणामी निकाय की कुल स्थिर वैद्युत ऊर्जा (पहले संधारित्र की तुलना में)
View Solutionसंलग्न चित्र 2.90 में X एवं Y अक्ष पर भौतिक राशियाँ प्रदर्शित करती हैं :

View Solutionधारिता `500muF` के संधारित्र को नियत दर `100muC//s` से आवेशित करते हैं । संधारित्र की प्लेटों के मध्य विभवान्तर 10 V होने में लगा समय होगा :
View Solutionयदि एक संधारित्र को आवेशित करते समय धारा नियत रखी जाती है तो संधारित्र पर विभव V तथा समय t के बीच खींचा गया ग्राफ होगा :
View Solutionएकसमान N बूँदों को एक ही विभव V पर आवेशित किया जाता है। वे एक-दूसरे से मिलकर एक बड़ी बूँद बनाती हैं। बड़ी बूँद का बिभव होगा :
View Solutionसमान त्रिज्या तथा समान आवेश की पारे की आठ बूँदें आपस में मिलकर एक बड़ी बूँद बनाती हैं। बड़ी बूँद की धारिता, प्रत्येक छोटी बूँद की धारिता की अपेक्षा है :
View Solutionत्रिज्या 2 सेमी की सर्वसम 64 बूँदों में प्रत्येक पर आवेश `10^(-9)` कूलॉम है। अब उन्हें संयुक्त कर एक बड़ी बूंद बनायी जाती है। इसका विभव होगा :
View Solutionअलग-अलग विभव पर आवेशित किए गये दो सर्वसम संधारित्र, स्त्रोतों से पृथक् करने के बाद, समान्तर क्रम में जोड़े जाते हैं। असत्य कथन है :
View Solutionदो गोलों A तथा B, जिनकी त्रिज्या क्रमशः 4 सेमी तथा 6 सेमी हैं, को आवेश `80muC` तथा `40muC` दिया गया है। इनको एक पतले तार से जोड़ने पर आवेश प्रवाहित होगा :
View Solutionदो सुचालक ठोस गोलों, जिनकी त्रिज्याएँ R व 2R हैं, को समान आवेश (+ Q) दिया जाता है। जय उन्हें आपस में एक पतले सुचालक तार से जोड़ा गया तो आवेश का पुनर्वितरण हो जाता है। अब छोटे गोले पर आवेश `Q_(1)` तथा बड़े गोले पर आवेश `Q_(2)` के बीच अनुपात होगा :
View Solutionदो गोलीय चालक जिनकी त्रिज्याएँ क्रमशः 1 मिमी तथा 2 मिमी हैं, समान आवेश Q से अलग-अलग आवेशित किये जाते हैं। इन्हें परस्पर सम्पर्क में रखने पर सन्तुलन अवस्था में इनके पृष्ठों पर विद्युत् क्षेत्र का अनुपात होगा :
View Solutionसमान आवेश 10 कूलॉम के त्रिज्या क्रमशः 20 सेमी और 15 सेमी के दो विद्युतुरोधित गोलों को एक ताँबे के तार से जोड़कर फिर अलग कर लिया जाता है, तो :
View Solutionदो सुचालक गोलों की त्रिज्याएँ `R_(1)` व `R_(2)` हैं तथा विद्युत् आवेश क्रमशः `Q_(1)` व `Q_(2)` हैं। इन्हें एक-दूसरे के सम्पर्क में लाने पर :
View Solutionसंधारित्रों का उपयोग ऐसे प्रत्यावर्ती विद्युत् परिपथ में किया जाता है जिसमें लगे विद्युत् संयन्त्र लेते हैं अधिक :
View Solutionसमान्तर प्लेट संधारित्र की धारिता निर्भर करती है:
View Solutionएक समान्तर पट्ट संधारित्र के बीच का स्थान मोटाई `d_(1)` और `d_(2)` और परावैद्यतांक क्रमशः `K_(1)` और `K_(2)` की दो पट्टियों से भरा है। यदि संधारित्र की पट्टियों के बीच की दरी d है तथा `d_(1) = d_(2) = d//2` तो संधारित्र की धारिता होगी :
View Solutionयदि किसी संधारित्र में वायु के स्थान पर परावैद्युतांक K का परावैद्युत पदार्थ रखा जाए, तो उस संधारित्र की धारिता :
View Solutionएक समान्तर पट्टिका संधारित्र पर आवेश q है तथा उसकी धारिता C है। पट्टिकाओं के बीच की दूरी दोगुनी करने में किया गया कार्य होगा :
View Solution
इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए questions and complete solutions for chapter विद्युत् विभव तथा धारिता of SHIVALAL AGARWAL AND CO PHYSICS (HINDI) of Class 12