एक विद्युत् क्षेत्र →E=30x2ˆi में x = 0 पर विभव V0 तथा x = 2 मीटर पर विभव VA के लिए VA−V0 का मान होगा :
80 V
120 V
−120V
−80V
Vx=−∫x0Edx=−∫0∞30x2dx
∴VA−V0=(−∫2∞30x2dx)−(−∫0∞30x2dx)=−∫2030x2dx=−30(x33)20=−80V
Topper's Solved these Questions
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् विभव तथा धारिता EXERCISE - अभ्यास222videos
विद्युत् विभव तथा धारिता
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विद्युत् आवेश तथा क्षेत्र EXERCISE - वस्तुनिष्ठ प्रश्न82videos
विद्युत् आवेश तथा क्षेत्र
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - विधुत-चुम्बकीय तरंगे EXERCISE - आंकिक प्रश्न3videos
विधुत-चुम्बकीय तरंगे
Similar Questions
यदि एक धनावेशित चालक को धात्विक तार द्वारा पृथ्वी से जोड़ा जाता है तो :
02:31View Solutionएक वस्तु पर 80 माइक्रो कूलॉम ऋण आवेश है। उस पर सामान्य अवस्था से अधिक इलेक्ट्रॉनों की संख्या होगी :
View Solutionसोडियम लाइट की तरंगदैध्य्र 5890Å है।इसकी आवृति ज्ञात कीजिए । प्रकाश का वेग =3×108 मीटर / सेकण्ड ।
View SolutionAssume that an electric field vec(E) = 30 x^(2) hat(i) exists in space. Then the potentail differences V_(A) - V_(0) where V_(0) is the potential at the origin and V_(A) , the potebntail at x = 2m is
04:45View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
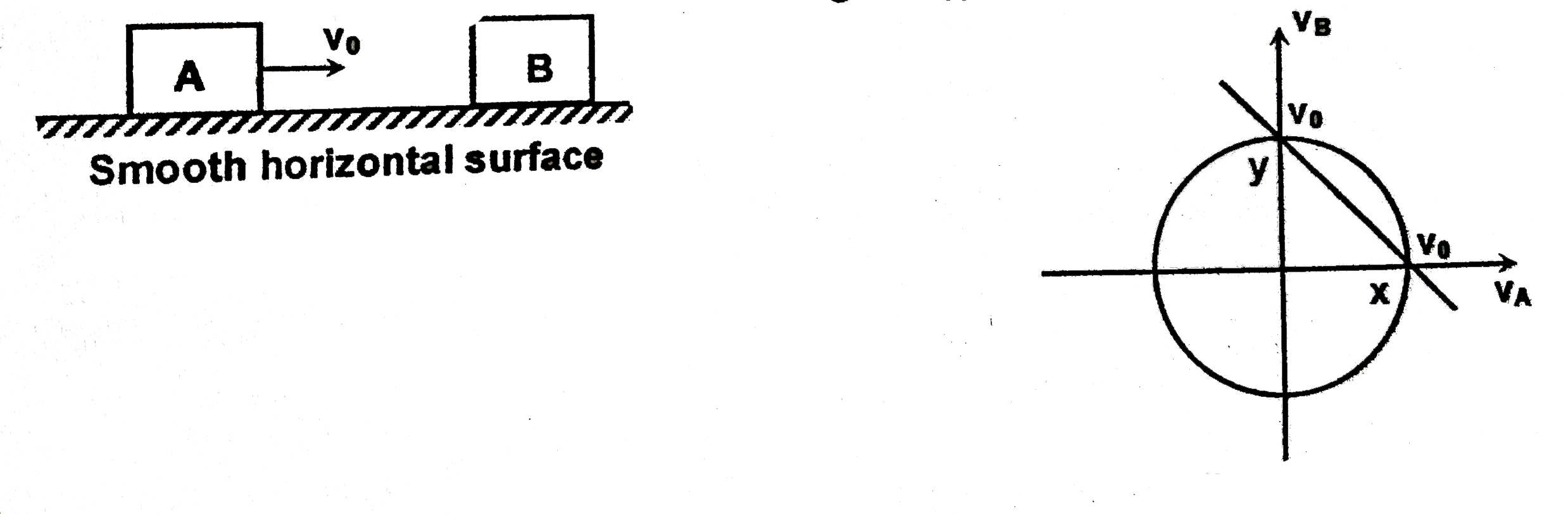
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is
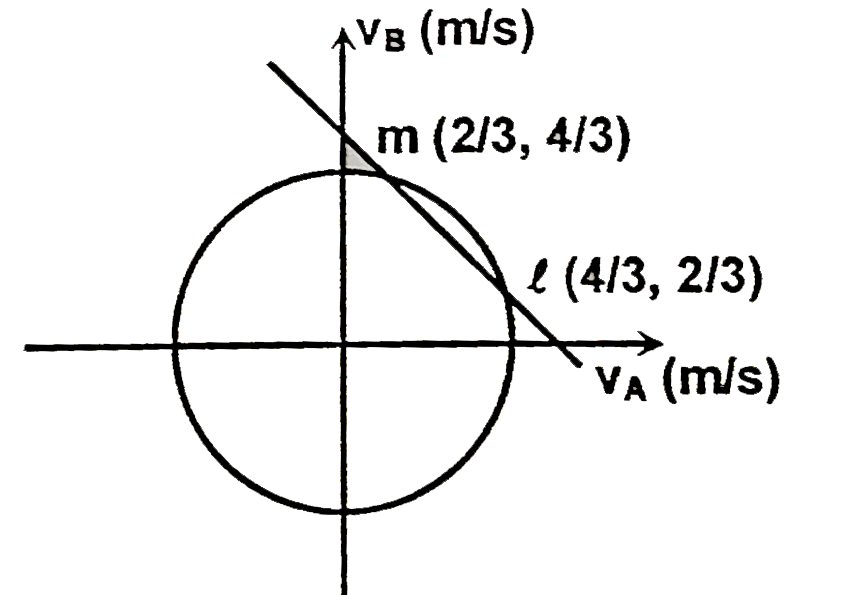 01:38View Solution
01:38View SolutionIn the circuit, shown in fig v_(s)=0.2V, v_(0)=-10V . Find v_(i) and gain A_(v)=v_(0)//v_(i) and A_(v)^(')=v_(0)/v_(s) ?
02:51View Solutionमाना व्योम में एक वैधुत क्षेत्र →E=30x2ˆi है तब विभवान्तर VA−V0, जहाँ V0 मूलबिंदु पर विभव एवं VA,x=2 मीटर पर विभव है
01:36View SolutionVm आयाम तथा ω0=1√LC आवृत्ति के विभव द्वारा चलित एक परिपथ अनुनादित होता है । गुणता कारण Q का मान होगा :
04:02View SolutionThe position of a particle at time t is given by the equation x(t) = V_(0)/A (1-e^(At)) V_(0) = constant and A > 0 Dimensions of V_(0) and A respectively are
04:20View SolutionA particle is moving along the x -axis with an acceleration a=3v^(2) .If the speed of the particle is v_(0) at x=0 ,which of the following is correct regarding final speed of the particle (A) (V_(0))/(e^(-3x)),v_(0)e^(x)],[" (C) "v_(0)x],[" (D) "v_(0)e^(3x)]]
01:25View SolutionThe position x of a particle at time t is given by : x=(v_(0))/(a)(1-e^(-at)) where v_(0) is a constant and a>0. The dimensional formula of v_(0) and a is :
02:06View SolutionAn electric field →E=10xhaii exists in a certain region of space. Then the potential difference V=V0−VA , where V0 is the potential at the origin and VA is the potential at x =2 m is …….. .
View SolutionThe position x of a particle at time t is given by x=V0a(1−e−at), where V0 is constant and a>0. The dimensions of V0 and a are
03:05View SolutionAssum that an electric field →E=30x2ˆiexists in space. Then the potential difference VA−V0, where V0 the potential at the origin and VA the potential at x = 2 m is :
03:16View SolutionA sphere of mass M1, moving with a velocity v0 collides head on with a stationary sphere of mass M2. The collision is elastic. V1 and V2 are respectively their velocities immediately after collision.
List - IList - II(a)M1=M2(e)V1=−V0,V2=0(b)M1<<M2(f)V1=0,V2=V0(c)M1>>M2(g)V0<V2<2V0(d)2M1>M1+M2(h)V1=V0,V2=2V0View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
44:26View Solution

